前面我们分析过的所有开关电源电路，很少提到电路过渡过程的概念，实际上，在开关电源电路中，工作开关的接通和关段，电路中电流和电压的变化过程，都是属于电路过渡过程，但我们为了分析简单，都把电路的过渡过程基本忽略掉了。如果认真对开关电源电路进行分析，输出电路中的电流一般都不是线性的或锯齿波；输出电压也不是一个矩形波或锯齿波，我们把它们当成矩形波或锯齿波，只是在一个特定条件或范围内，把它们的变化率或数值当成了一个平均值来看待。

在具有电感、电容、电阻的电路中，发生电路过渡过程的电压、电流一般都是按指数函数的曲线规律变化，正弦或者余弦函数是指数函数的特殊情况。在具有过渡过程的电路中，我们不能简单地用正弦波电路的计算方法来分析，用付氏变换的方法也很难分析出精确结果。用微分方程对电路过渡过程进行分析是最好的方法。

在电路的过渡过程中，一定要考虑电压或电流的初始值，只有当初始值基本为0或趋于某个固定值时，才可认为电路的过渡过程已经进入稳定状态，但严格来说，这种情况在开关电源电路中不存在。因为，开关电源中的工作开关总是不断地在接通与关断两中工作状态之间来回转换，并且占空比D时刻都在改变，它不可能出现一个稳定值。然而，我们可以把开关电源当成一种特殊情况来处理，或把开关电源电路中，电压或电流的初始值反复出现时，就可以认为开关电源已经工作于稳定状态。

例如，当开关电源在一个或两个工作周期内，对应于工作开关接通或关闭的瞬间，某电路的电压或电流的初始值基本相等，或很接近时，我们就可以认为，开关电源已经进入了稳定工作状态。

当开关电源进入工作稳定状态以后，为了简单，我们一般都用电压或电流的其平均值或半波平均值来进行电路电路计算或分析。例如，我们在计算流过负载的电流时，一般都是利用输出电压的平均值Uo来进行计算，很少考虑输出电压纹波对负载的影响，计算负载电流的结果就是流过负载电流的平均值Io。

然而，在开关电源的设计中，开关电源开机时刻的过渡过程也是不可忽视的，因为，储能滤波电容存储的电荷为0，需要很多个工作周期以后，储能滤波电容才能充满电，其两端电压才基本稳定，开关电源才能进入稳定工作状态。下面，我们来详细分析开关电源开机时刻的过渡过程。
  

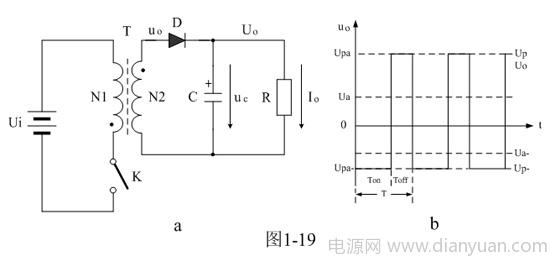
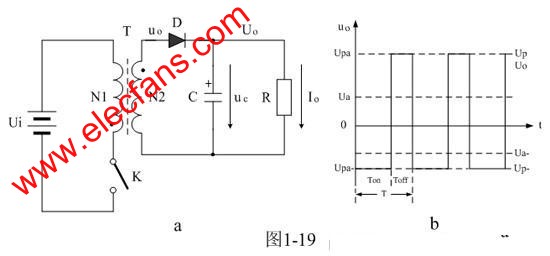
图1-19中，当工作开关由接通转为关断时，开关电源变压器次级线圈产生的反电动势为：

式中，q为电容存储的电荷量，C1和C2为待定系数，ω =  ，为角频率，即电容器充放电的速率。这里为了简化在不容易混淆的情况下我们经常把电感L和电容C的下标省去。

当t = 0 时，q = 0，由此求得C1 = 0，当t = Toff时，由于电容容量很大，电容器一般在一个工作周期内是不可能充满电的，大约需要十几个周期以上才能充满。当电容充满电时，电容两端的电压就可以达到电源电压的峰值，即：q = UpC，由此，求得C2 = UpC，所以（1-112）式可以写为：这里特别指出，（1-112）、（1-113）、（1-114）式中的时间t对于电容器充电来说是不连续的，它是按正弦曲线一段、一段地进行迭加，如图23。
 

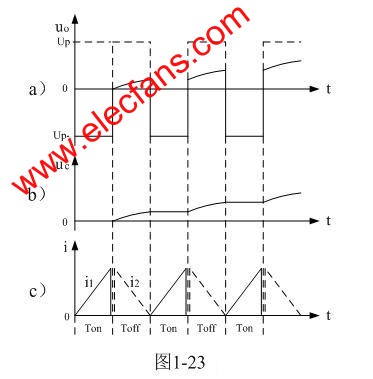
图1-23-a）中，uo为变压器次级线圈输出电压的脉冲波形，虚线是整流之前变压器次级线圈的输出波形（半波平均值），实线是实际输出波形，由于整流二极管的限幅作用，所以实际输出电压幅度要比正常工作时低很多。在每次工作开关由接通转变为关断期间，变压器次级线圈的输出电压，都经整流二极管对储能滤波电容进行充电，使储能滤波电容两端的电压一步、一步地升高，输出电压幅度也一步、一步地升高。

图1-23-b）是储能滤波电容器进行充电的电压波形，它需要经过多个工作周期后才能对储能滤波电容充满电，因此，储能滤波电容两端的电压是按正弦曲线，像爬楼梯一样，一个、一个楼梯一样提升，直到储能滤波电容两端的电压达到最大值Up。

图1-23-c），是变压器初、次级线圈的电流波形。图中，i1为流过变压器初级线圈中的电流，i2为流过变压器次级线圈中的电流（虚线所示）。实际上流过变压器次级线圈中的电流i2也不是线性下降，而是按余弦或指数曲线变化，但由于其曲率变化很小，所以我们把它近似地看成是一根直线，或用其变化率的平均值来代替，以便与输出电压波形（矩形波）对应。

前面我们分析过的所有开关电源电路，很少提到电路过渡过程的概念，实际上，在开关电源电路中，工作开关的接通和关段，电路中电流和电压的变化过程，都是属于电路过渡过程，但我们为了分析简单，都把电路的过渡过程基本忽略掉了。如果认真对开关电源电路进行分析，输出电路中的电流一般都不是线性的或锯齿波；输出电压也不是一个矩形波或锯齿波，我们把它们当成矩形波或锯齿波，只是在一个特定条件或范围内，把它们的变化率或数值当成了一个平均值来看待。

在具有电感、电容、电阻的电路中，发生电路过渡过程的电压、电流一般都是按指数函数的曲线规律变化，正弦或者余弦函数是指数函数的特殊情况。在具有过渡过程的电路中，我们不能简单地用正弦波电路的计算方法来分析，用付氏变换的方法也很难分析出精确结果。用微分方程对电路过渡过程进行分析是最好的方法。

在电路的过渡过程中，一定要考虑电压或电流的初始值，只有当初始值基本为0或趋于某个固定值时，才可认为电路的过渡过程已经进入稳定状态，但严格来说，这种情况在开关电源电路中不存在。因为，开关电源中的工作开关总是不断地在接通与关断两中工作状态之间来回转换，并且占空比D时刻都在改变，它不可能出现一个稳定值。然而，我们可以把开关电源当成一种特殊情况来处理，或把开关电源电路中，电压或电流的初始值反复出现时，就可以认为开关电源已经工作于稳定状态。

例如，当开关电源在一个或两个工作周期内，对应于工作开关接通或关闭的瞬间，某电路的电压或电流的初始值基本相等，或很接近时，我们就可以认为，开关电源已经进入了稳定工作状态。

当开关电源进入工作稳定状态以后，为了简单，我们一般都用电压或电流的其平均值或半波平均值来进行电路电路计算或分析。例如，我们在计算流过负载的电流时，一般都是利用输出电压的平均值Uo来进行计算，很少考虑输出电压纹波对负载的影响，计算负载电流的结果就是流过负载电流的平均值Io。

然而，在开关电源的设计中，开关电源开机时刻的过渡过程也是不可忽视的，因为，储能滤波电容存储的电荷为0，需要很多个工作周期以后，储能滤波电容才能充满电，其两端电压才基本稳定，开关电源才能进入稳定工作状态。下面，我们来详细分析开关电源开机时刻的过渡过程。
  

图1-19中，当工作开关由接通转为关断时，开关电源变压器次级线圈产生的反电动势为：

式中，q为电容存储的电荷量，C1和C2为待定系数，ω =  ，为角频率，即电容器充放电的速率。这里为了简化在不容易混淆的情况下我们经常把电感L和电容C的下标省去。

当t = 0 时，q = 0，由此求得C1 = 0，当t = Toff时，由于电容容量很大，电容器一般在一个工作周期内是不可能充满电的，大约需要十几个周期以上才能充满。当电容充满电时，电容两端的电压就可以达到电源电压的峰值，即：q = UpC，由此，求得C2 = UpC，所以（1-112）式可以写为：这里特别指出，（1-112）、（1-113）、（1-114）式中的时间t对于电容器充电来说是不连续的，它是按正弦曲线一段、一段地进行迭加，如图23。
 

图1-23-a）中，uo为变压器次级线圈输出电压的脉冲波形，虚线是整流之前变压器次级线圈的输出波形（半波平均值），实线是实际输出波形，由于整流二极管的限幅作用，所以实际输出电压幅度要比正常工作时低很多。在每次工作开关由接通转变为关断期间，变压器次级线圈的输出电压，都经整流二极管对储能滤波电容进行充电，使储能滤波电容两端的电压一步、一步地升高，输出电压幅度也一步、一步地升高。

图1-23-b）是储能滤波电容器进行充电的电压波形，它需要经过多个工作周期后才能对储能滤波电容充满电，因此，储能滤波电容两端的电压是按正弦曲线，像爬楼梯一样，一个、一个楼梯一样提升，直到储能滤波电容两端的电压达到最大值Up。

图1-23-c），是变压器初、次级线圈的电流波形。图中，i1为流过变压器初级线圈中的电流，i2为流过变压器次级线圈中的电流（虚线所示）。实际上流过变压器次级线圈中的电流i2也不是线性下降，而是按余弦或指数曲线变化，但由于其曲率变化很小，所以我们把它近似地看成是一根直线，或用其变化率的平均值来代替，以便与输出电压波形（矩形波）对应。