摘 要: 用微粒群优化算法解决存在约束的广义预测控制的优化问题,并给出了基于微粒群优化算法的广义预测控制算法的实现方法。将该算法应用到工业过程对象中进行测试,仿真结果表明了算法的有效性和高效性,获得了良好的控制效果。
关键词: 广义预测控制;遗传算法;优化;约束
广义预测控制已经在工业过程中得到广泛应用。在广义预测控制中,如果被控过程是线性无约束的,并且目标函数是二次型的形式,则可求得一个解析的线性控制器,但是实际工业过程中存在着各种约束,这会使求解控制量的滚动优化问题变得复杂,通常需求解一个有约束的二次规划或非凸规划,而传统的通过迭代求解二次规划和非凸规划方法计算量非常大,另外非凸规划的求解对初始条件也非常敏感,这些会影响到广义预测控制的性能。为了解决此问题,本文将粒子群优化算法应用到广义预测控制中,解决广义预测控制的局限性。
1 广义预测控制算法
广义预测控制算法是一种先进的控制算法,它广泛应用在电力、炼油、化工和造纸等工业领域,是一种源于实际工业过程的高级控制算法,是预测控制中最具代表性的算法之一[1-4],随着对广义预测控制研究的不断深入,其理论和算法也逐步得到了完善。在广义预测控制算法中,用受控自回归积分滑动平均(CARMA)模型描述一个具有非平稳噪声的实际过程可表示为:


式(19)中,如果控制量存在约束情况,则需求解带有约束的二次规划,约束非线性的存在会导致优化成为一个非凸规划,非凸规划的求解对初始条件非常敏感,会在局部最优解处收敛,无法保证求得的是全局最优解,本文尝试用微粒群优化(PSO)算法来解决这一局限性。
2 PSO算法及其改进
2.1 基本PSO算法原理
由Kennedy和Eberhart提出的PSO算法[5-7]来源于对简单社会的模拟,最初设想是模拟对鸟群觅食的过程,后来发现PSO算法是一种很好的优化工具。PSO算法与其他进化算法相类似,也是将寻优的参数组合成群体,通过对环境的适应度来将群体中的个体向更好的区域移动。与其他进化算法不同,在描述个体时,将其看成是D维寻优搜索空间的一个没有体积的微粒(点)[8-10],结合微粒的历史最佳位置和群体历史中最优微粒的最佳位置信息,按追随最优微粒的原理,以一定的速度向目标值逼近。

一代提供信息,使粒子获得的信息量增大,从而可能更快地找到最优解。同时Pn的权重系数很小,相当于扰动信息,增加了粒子的多样性,避免算法过早收敛。式(21)和式(22)组成后称之为改进的PSO算法(MPSO)。
2.3 算法设计
引入了约束的广义预测控制问题,实际上就是一个非线性优化问题,利用PSO算法对其进行处理的基本思想是:首先通过选择合适的适应度函数,将有约束广义预测控制性能指标优化的极小值问题转化为PSO算法优化的极大值问题;然后通过空间限定法引入约束,经迭代计算后最终得到满足约束的最优控制量求解。
基于MPSO算法的广义预测控制结构如图1所示,预测模型采用式(12)的形式,MPSO算法通过优化性能指标J(t)输出控制量进行控制。

对优化性能指标进行变换得到适应度函数为:

式中,J(t)可以是式(18)的形式,也可以是满足控制性能要求的其他形式,通过这种变换将GPC优化的极小值问题转化为MPSO算法优化的极大值问题,并使MPSO算法的适应度函数值都在区间[0,1]中变化。
3 仿真实例
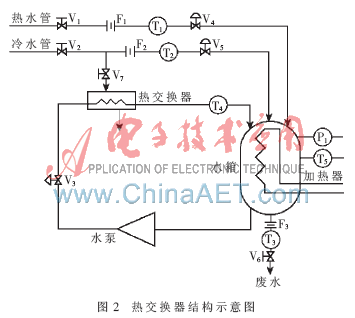
热交换器是工业生产所需要的一种换热装置,结构如图2所示,图中,T1、T2、T3、T4、T5均为温度控制器,F1、F2、F3均为测量流量的控制器,P1为测量压力的控制器。系统中包括2个输入管,即1个热水管和1个冷水管,对应控制其流量的阀门为V1、V2。另外还有1个15 kW的隔热式加热水箱。水箱中的温度通过冷水管中的流量来控制,而水箱中的水又经过1个离心泵,通过阀门V3来控制,输送回热交换器中。这其中包括很多闭环控制系统,被测量有温度、流量、压力等,本文选择的闭环系统为热交换器中循环水的温度控制,对温度控制回路的扰动主要有蒸汽压力、水流速度和进水温度。本文选取的闭环控制为图2中的T4-V3环节。

本文尝试用微利群优化算法来解决该非线性优化问题,从仿真结果来看,该算法具有良好的鲁棒性和跟踪性能,取得了满意的控制效果,表明将粒子群优化算法应用到广义预测控制中是可行和有效的。
参考文献
[1] MENDES J,KENNEDY J, NEVES J.Watch the neighbor or how the swarm can learn from its environment[C].Proc.Of the IEEE Swarm Intelligence Symposium.Indiana: IEEE Press, 2003:88-94.
[2] CLARKE D W.Generalized predictive control-part I[J]. Automatica,1987,23(2):137-148.
[3] CLARKE D W.Generalized predictive control-part II extensions and interpretations[J].Automatica,1987,23(2):149-160.
[4] 王伟.广义预测控制理论及其应用[M].北京: 科学出版社,1998.
[5] KENNEDY J, EBERHART R.Particle swarm optimization[C]. Proc.IEEE Int.Conf.on Neural Networks.Perth: IEEE Press,1995:1942-948.
[6] SHI Yu Hui, EBERHART R.A modified particle swarm optimizer[C].Proc.IEEE Int.Conf.on Evolutionary Computation.Anchorage: IEEE Press,1997:303-308.
[7] ZHANG L P, YU H J, HU S X.A new approach to improve particle swarm optimization[C].Proc.Of the Genetic and Evolutionary Computation Conf.Chicago: IEEE Press, 2003:134-142.
[8] MILLONAS M M.Swarms phase transition and collective intelligence[M].MA: Addison Wesley, 1994.
[9] SHI Y,EBERHART R C.Fuzzy adaptive particle swarm optimization[C].Proc.Of the IEEE Congress on Evolutionary computation.Seoul,Korea:IEEE Press, 2001:101-106.
[10] RATNAWEERA A, HALGAMUGE SK, WATSON C.Selforganizing hierarchical particle swarm optimizer with timevarying acceleration coefficient[C].IEEE Trans.Evolutionary computation.IEEE Press, 2004:240-255.

