摘  要： 基于N阱 0.6μm DPDM CMOS工艺，完成了高阶∑△ADC中第一级积分器的设计。分析了开关电容" title="开关电容">开关电容积分器的非理想特性，同时设计了一个对寄生电容" title="寄生电容">寄生电容不敏感的同相开关电容（SC）积分器，并特别采用旁路电容" title="旁路电容">旁路电容减小沟道电荷注入引起的谐波失真和噪声。在cadence下的电路仿真表明，积分器具有-104.9dB等效输入噪声；利用MATLAB进行系统仿真，∑△ADC的信号噪声畸变比（SNDR）达到100.5dB，满足系统16bit的要求。 

    关键词： 开关电容；积分器；电荷注入；共模" title="共模">共模反馈 

    在现代信号处理中，由于CMOS工艺中的电阻和电容的绝对容差大及面积上的约束，不能满足大多数信号连续处理的要求。开关电容积分器利用周期性的翻转电容形成等效电阻，实现了模拟信号的离散处理。而开关电容电路具有准确的频率相应、良好的电压线性度和温度特性等特点，并易于与CMOS工艺兼容，因此，∑△ADC中的调制器主要使用开关电容电路来实现。因为调制器的性能决定了ADC的转换精度，作为调制器中的基本模块，积分器的设计更是至关重要。 

    本文基于N阱0.6DPDM CMOS工艺，完成了五阶∑△ADC中第一级积分器的设计，电路采用对寄生电容不敏感的同相开关电容（SC）积分器结构，并使用两相非重叠时钟和旁路电容减小电荷注入引入的谐波失真和噪声。而积分器中所使用的折叠式共源共栅放大器减小了积分器的非理想特性。经过仿真验证，积分器具有-104.9dB的等效输入噪声，∑△ADC的SNDR达到100.5dB，满足系统16bit精度的要求。 

1 开关电容积分器 

1.1 开关电容积分器的基本原理 

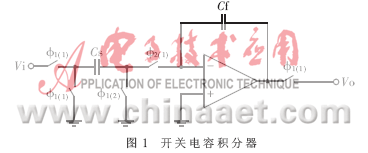
    现在广泛使用的积分器为同相积分器和反相积分器，其结构如图1所示。其中Cs为采样电容；Cf为积分电容；Ф1和Ф2为两相非重叠时钟，括号外为同相积分器电路时钟，括号内为反相积分器电路时钟。根据积分器和离散信号的工作原理，同相积分器的传输函数为： 

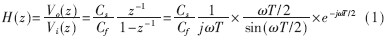
其中，ω为信号角频率；一个离散信号延时z^-1对应一个时钟周期T，每个时钟周期分为采样相位和积分相位。式(1)中的第一部分为理想积分器的表达式，第二部分为幅度误差，第三部分为相位误差。信号的频率越高，积分器的误差越大，因此时钟频率应取较大值，从而减小信号频率对误差的影响（后面的所有推导都是基于同相积分器进行）。 

1.2 开关电容积分器的非理想特性 

    积分器的非理想特性包括时钟馈通、运算放大器的有限查摸增益、有限单位增益带宽以及摆率，而时钟跳变也会对积分器性能产生影响，具体分析可参考相关资料^[2]。 

    考虑运放" title="运放">运放的有限增益后，积分器中运放的输入端不再虚短，这时运放的寄生电容也必须加以考虑，这会带来积分器的电荷泄漏（charge leakage），即采样电容上的电荷在电荷转移周期内并没有完全转移到积分电容上，而是泄漏到一些寄生电容里。设运放的有限增益为A，运放的寄生电容为Cp，采用如图2所示的等效模型进行分析。根据电荷守恒原理，可得： 

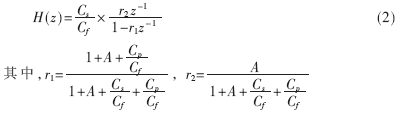
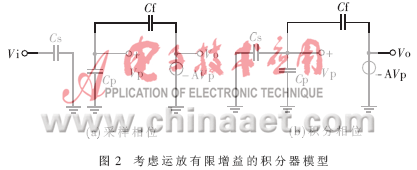
    积分器传递函数的极点误差为（1－r₁），增益误差为（1－r₂）。极点误差可使积分器极点偏离单位圆，引起调制器传输函数的改变，并产生电荷泄露而引入静态误差，从而增加调制器噪声水平。开关电容积分器的建立过程也并不像理想转换过程那样完美，运放的有限带宽会让积分器转换过程在有限时间内产生动态误差。假设运放的有限带宽为B，则传输函数可写为： 

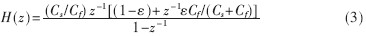
其中，ε=e^-πBTS，T为时钟周期^[1]。从上式可知，运放带宽越大引入的误差就越小。在通常情况下，开关电容积分器中运放的单位增益带宽应至少大于采样频率的10倍^[2]。运放的摆率同样重要，当积分电容上的电荷变化引起运放的输出电压变化时，有限摆率会产生影响。为了避免这个影响，必须满足Vo/SR[3]。 

    开关电容电路中的开关为MOS开关，其存在着“沟道电荷注入”现象和时钟馈通效应，并具有有限的导通电阻和漏电流。目前普遍采用CMOS开关和全差分电路及两相非重叠时钟技术来减小这些非理想特性的影响^[1]。 

2 电路实现 

2.1 运放的设计 

    由前面的分析可知，为了使积分器完全建立，并提高∑△调制器的过采样率，速度是运放主要考虑的因素。折叠式共源共栅能提供中等程度的增益，同时，它具有较大的带宽和共模输出范围，故被广泛应用于开关电容积分器的设计中。本文所设计的运放电路结构如图3所示。 

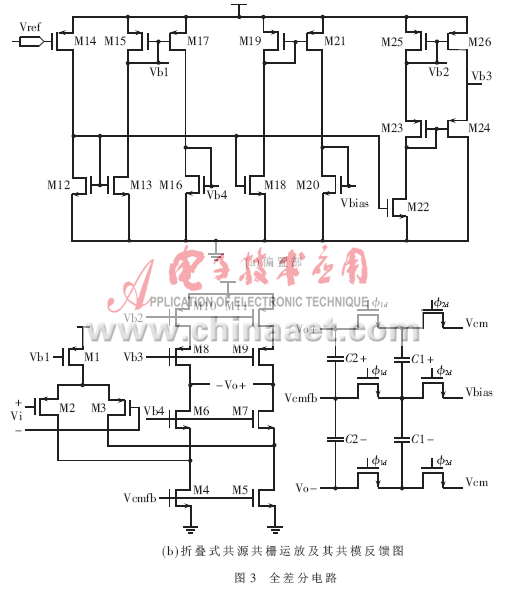
    折叠式共源共栅的增益由式(4)决定： 

    由于在∑△调制器中，第一级积分器的噪声不能被整形，故需减小其输出噪声。所以，本文采用噪声较小的PMOS作为输入差分对，而靠近电源和地的四个MOS管取较大的栅长，在此取3μm。 

    全差分运放需要共模负反馈网络来稳定输出共模电压。开关电容共模反馈使用电容和两相非重叠时钟实现了共模反馈的功能，并不消耗额外的功耗。CMFB通过非重叠时钟对开关电容进行不断的刷新来稳定共模输出电压。图3（b）为开关电容共模反馈结构，其中C1+和C1-检测共模电压，C2+和C2-将检测到的电压与运放输出电压比较，然后根据比较结果反馈一个共模输出电压： 

    V_cmfb调整运放偏置电流源。C1和C2的比值决定在周期之间步长的幅度，它会导致不同的收敛速度，比值越大收敛越快。然而，C1的增大会降低放大器的频率特性，而太小的C1则增加了积分器的稳定时间，也会增大输出共模电压的误差^[4]。基于以上考虑，C1＝100fF，C2＝600fF。 

2.2 积分器的设计 

    根据前面的理论分析，为了减小沟道电荷注入等非理想效应引起的误差和噪声，开关电容积分器采用了对寄生电容不敏感的全差分同相积分器和“下极板采样”技术，其电路结构如图4所示，图中Ф1a和Ф2a分别是Ф1和Ф2的延时相时钟。 

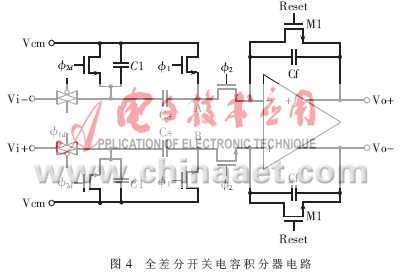
    在一阶近似中，当Ф2关断时，其源端和漏端总是接地，所以，其注入和吸收的电荷为常数，与Vi无关，而仅引入失调电压，并可通过全差分电路来消除。但是，在二阶近似中，当Ф1导通时，使Ф2吸收的总沟道电荷独立于信号，而当其断开时注入的电荷却由开关两边的阻抗决定。因为CMOS传输门的阻抗和输入信号有关，故Ф2的注入电荷与信号相关，从而引入了谐波失真。因此，可在采样电容的左端和共模电平之间连接一个旁路电容C1。如果CMOS传输门和旁路电容的RC常数大于关断Ф1时钟的下降时间，则当Ф1断开时所看到的阻抗由旁路电容决定，由于旁路电容的阻抗不变，故消除了失真。C1的电荷注入会被和其并联的开关消除。为了协调系统的工作和控制，利用M1作为Reset开关。 

    采样电容和积分电容主要由积分器的噪声大小来决定，积分器理想输入热噪声为：S_N＝4KT/C_s，所以应采用较大的采样电容；但较小的采样电容有利于减小运放的容性负载，使得运放有更好的转换速率，更节约了芯片面积。所以，C_s＝525fF，C_f＝7.6pF，积分器的积分频率为C_s/(C_f×T)。 

3 仿真验证 

3.1 电路仿真 

    采用CSMC 0.6μm DPDM CMOS工艺库，在cadence中对电路进行仿真，验证运放和积分器的性能。仿真条件为：电源电压V_DD=5V，时钟频率f_CLK=2.5MHz，负载电容C_L=1pF。运放的性能参数如表1所示；积分器的仿真结果如图5所示^[5]。由仿真结果可得：积分器的积分频率为175.59kHz，而理论值为172.69kHz，所以积分器的幅度误差仅为0.016；相位误差满足±100的频率为15Hz～108.33kHz，满足音频信号处理的需要。积分器等效输入噪声为-104.9dB。

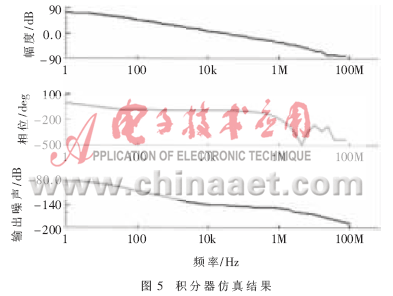
3.2 系统仿真 

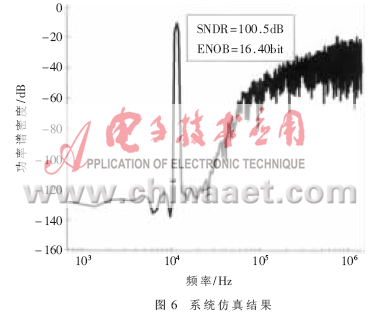
    在MATLAB中利用Simulink建立五阶∑△ADC系统模型。理想模型的仿真得到：SNDR＝117.7dB，有效位数ENOB＝19.26bit；考虑积分器非理想特性的影响，仿真结果为：SNDR＝114.1dB，ENOB＝18.66bit；仅考虑积分器噪声的仿真结果为：SNDR＝110.6dB，ENOB＝18.08bit；最后，同时考虑这两种因素的影响，得到SNDR为107.9dB，ENOB达到17.64bit。系统最后的仿真结果如图6所示。∑△ADC的有效位数达到16.40bit，满足系统设计16bit的要求。 

    本文详细讨论了开关电容积分器的非理想特性，在此基础上采用对寄生电容不敏感的同相积分器结构，利用非重叠时钟和旁路电容减小电荷注入引入的失真和噪声，从而完成了高阶∑△ADC中的第一级积分器的设计。经过系统仿真验证，∑△ADC的SNDR达到100.5dB，ENOB达到16.40bits，满足系统设计要求。 

参考文献 

[1] NORSWORTHY SR，SCHREIER R，TEMES GC.Delta-Sig ma Data Converters，Theory，Design and Simulation.Wiley：IEEE Press，1996.333-356. 

[2] PATRAS GB，ATHENS AP，PATRAS VA.Delta-Sigma Modulators：modling，Design and Applications.London：Imperial College Press，2003，139-152. 

[3] BOSER B，WOOLEY BA.The Design of Sigma-Delta Modulation Analog to Digital Converters.IEEE Journal SolidState Circuits，1988，23(12)，1298-1308. 

[4] CHOKSI O，CARLEY LR.Analysis of Switched-capacitor Commom-mode Feedback Circuit.IEEE Tanscation on circuit and system-II：analog and digital processing，2003，50(12)：906-917. 

[5] KUNDERT K.Simulation switched-capacitor filters with spectreRF.v6c，28，2006(7).http：//www.designers-guide.com/Analysis/scfilters.pdf.