一种MQAM调制器的设计与实现
2008-10-22
作者:朱冰莲 梁立宏
摘 要: 提出了一种利用FIR滤波器系数对称性、CSD编码和数据选择器" title="数据选择器">数据选择器简化MQAM调制器设计的新方法。用该方法在FPGA上实现4、16、64、256QAM调制器。实验证明该方法在硬件资源消耗和工作时钟频率方面都有较大的改善。
关键词: 多电平正交振幅调制(MQAM) FIR CSD
随着移动用户数量的不断增加和人们对图像等多媒体信息的通信要求,传统通信系统的容量已经越来越不能满足要求,而可用频谱资源有限,也不能靠无限增加频道数目来解决系统容量问题。确定一种高频谱利用率的调制方案能在很大程度上解决这一问题。多电平正交振幅调制(Multilevel Quadrature Amplitude Modulation)是一种具有高频谱利用率的调制技木[1]。在无线通信中,它可以根据信道的衰落程度、信道流量等参数动态改变调制方式,提高信道利用率和信息传输速率。这种高效的数据传输方式实现的关键是FIR(Finite Impulse Response)滤波器和数字混频器" title="混频器">混频器的设计,它们通常限制了调制器的速率。本文采用基于CSD(Canonic Signed Digit)编码的FIR滤波器,并利用FIR滤波器系数对称性、数据选择器实现模块重用,简化MQAM调制器设计,既节约了硬件资源又提高了器件的工作频率" title="工作频率">工作频率。
1 MQAM调制器设计
MQAM调制框图[2]如图1所示。
MQAM和调制器由串并转换" title="串并转换">串并转换、IQ分路、脉冲形成和调制混频单元组成。串并转换单元将串行的数据流转化为并行的数据流;IQ分路单元根据不同的调制星座要求,将输入的信号分解成同相和正交分量(I路和Q路信号分量);脉冲形成滤波器对I、Q两路信号进行波形形成;调制混频单元对I、Q两路信号进行混频、合成,形成调制信号输出。
1.1 串并转换
串并转换通过log2 M级移位寄存器实现,调制方式控制字控制串并转换单元的工作时钟频率。若数据输入的速率为f,则串并转换单元的工作频率是f/log2 M。输入数据按log2 M个比特一组起作用,输入的二进制数据分别进入log2 M个信道,每个信道的比特率等于输入比特速率的1/log2 M,log2 M比特串行输入比特分离器,然后同时并行输出,信号进入IQ分路单元。
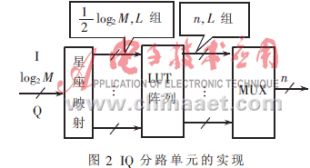
1.2 IQ分路单元
图2是IQ分路的实现框图。L为输入和输出查找表" title="查找表">查找表的数据线组数,数值上等于MQAM调制器的调制方式种数,如实现4、16、64、256QAM调制器,则L=4。宽度为log2 M的数据输入星座映射模块,根据调制方式控制字,星座映射的L组输出线中,相应的一组起作用,输入数据被映射为宽度为![]() log2 M的数据输出,作为查找表阵列中对应查找表的地址输入。查找表中存储的是与调制方式对应的数据,位宽n根据需要的精度设定。由于I、Q两路查找表数据一样,可以控制在不同的时刻使星座映射单元映射输出不同的地址,使I、Q两路使用同一个查找表,这样星座映射单元输出数据的频率为2f/log2 M,I、Q两路的输出相差一个查找表的工作时钟。最后,数据选择器根据控制字选择一组作为IQ分路单元的输出。
log2 M的数据输出,作为查找表阵列中对应查找表的地址输入。查找表中存储的是与调制方式对应的数据,位宽n根据需要的精度设定。由于I、Q两路查找表数据一样,可以控制在不同的时刻使星座映射单元映射输出不同的地址,使I、Q两路使用同一个查找表,这样星座映射单元输出数据的频率为2f/log2 M,I、Q两路的输出相差一个查找表的工作时钟。最后,数据选择器根据控制字选择一组作为IQ分路单元的输出。
1.3 脉冲形成滤波器
脉冲形成滤波器采用FIR滤波器,FIR滤波器公式[3]:

FIR滤波器的系数是偶对称或者奇对称,即有:
h(n)=h(N-1-n)(偶对称)或者h(n)=-h(N-1-n)(奇对称) (2)
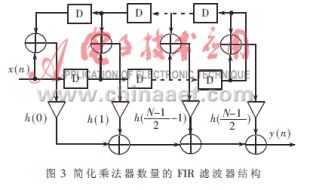
利用系数对称性减少乘法器数量的FIR滤波器结构如图3所示。
在滤波器参数确定后,系数是一个固定值,所以滤波器的所有乘法都是固定系数乘法。实现固定系数乘法就可以用移位、加/减来代替并行乘法。任何滤波器系数都可表示成CSD码[4~5]的形式,这样加减法的次数就可以达到最少,对理想滤波器的系数进行CSD量化可简化硬件实现时乘法器部分的结构。
二进制补码与CSD编码的转换方法如下:
一个数X=x(n-1)x(n-2)…x(0),如果对于所有i=0,1,...,n-1,x(i) =0,1,或-1,且对于所有i=1,…,n-1,满足x(i)x(i-1)=0,则X=x(n-1)x(n-2)…x(0)称为X的CSD编码表示。
一个数的CSD表示中的非0比特位总是不相邻的,用一个2bit的二进制数表示一个CSD码中的非0比特数,01代表+1,11代表-1(最高位通过符号位扩展实现),则可以将一个数的CSD编码表示转换为二进制CSD编码(BCSD)表示。二者具有一一对应关系。根据上述原理,一种将二进制补码数变换得到其CSD编码表示的过程描述为:首先将二进制补码表示转换为称为BCSD编码的表示,然后按照01代表+1,11代表-1相反的过程转换BCSD编码得到数的CSD编码表示。一种将二进制补码数转换得到BCSD编码的算法描述如下:
(1)初始化:输入X=x(n-1)x(n-2)…x(0);符号扩展x(n)=x(n-1);计数器置0(i=0);标志位置0(f=0)。
(2)循环执行下列语句:如果i>n-1,则跳转到(3),否则继续执行下列语句:
①如果f=0:如果x(i+1)x(i)=11,则f=1,i=i+2;如果x(i+1)x(i)=01,则f=0,i=i+2;否则,f=0,i=i+1。
②如果f=1:如果x(i+1)x(i)=00,则f=0,x(i)=1,i=i+2;如果x(i+1)x(i)=10,则f=1,x(i)=1,i=i+2;否则,f=0,x(i)=0,i=i+1。
③返回到(2)。
(3)如果f=1,则x(i)=!x(i);否则,x(i)=x(i)。
(4)结束。
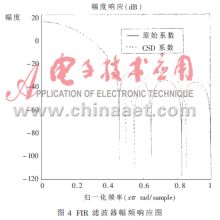
本文采用12抽头hamming形式的低通滤波器,截止频率为0.15。为了便于CSD量化,将最大滤波器系数归一化,其余各系数也乘以相应的常数,滤波器特性没有改变。表1是滤波器系数,图4是原始系数与CSD编码系数FIR滤波器幅频响应图。
1.4 调制混频器的设计
混频器输出信号[6]为:
s(k)=I(k)cos(2πkfc/fd)+Q(k)sin(2πkfc/fd) (3)
其中,fd为DDS的工作频率,当fd=4 fc时,得到:
s(k)=I(k)cos(πk/2)+Q(k)sin(πk/2) (4)
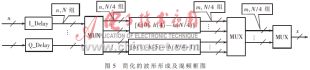
以上两式中,1≤k≤∞,cos(πk/2)可以表示为1,0,-1,0…的序列,sin(πk/2)可以表示为0,1,0,-1...的序列。设同相路I(f)的样本序列I(k)为I1,I2,I3…,正交路Q(f)的样本序列Q(k)为Q1,Q2,Q3…,则S(k)的样本序列为I1,Q2,-I3,-Q4,I5,Q6…。这样,正交调制就可以简化成子滤波器和数据选择器构成。如图5所示,输出由每一个时刻使能不同的子滤波器得到。这种结构适合高速设计,而且占用硬件资源少,输出时钟是子滤波器时钟的2倍。
其中,N为滤波器的抽头数,又由上面的分析可以知道输出序列可以表示为:
h(0)x(n)+h(4)x(n-4)+h(8)x(n-8)+…(5)
h(1)x(n-1)+h(5)x(n-5)+h(9)x(n-9)+…(6)
-h(2)x(n-2)-h(6)x(n-6)-h(10)x(n-10)-…(7)
-h(3)x(n-3)-h(7)x(n-7)-h(11)x(n-11)-… (8)
综合(2)(5)(6)(7)(8)可以看出,(5)(8)可以用同一组滤波器实现,(6)(7)可以用同一组滤波器实现,滤波器组的输入是N/4组宽度为n的数据,输出是 N/4组宽度为m的数据,m与查找表和滤波器系数的位宽有关,利用数据选择器选择一组滤波器组输出送到加法器,最后即为调制混频输出,位宽x根据需要确定。
2 MQAM调制器各部分工作时钟
MQAM调制器各模块工作时钟关系如图6所示。
输入速率为f的串行数据流,经过工作时钟为f1=f/log2 M的串并转换单元,得到速率为f1的并行数据流,经过查找表LUT、数据选择器MUX和延时单元Delay之后的数据选择器以f1的时钟频率工作,输出数据分别进入两个滤波器组,以2 f1时钟工作的数据选择器交替把滤波器组的输出送给后级加法器单元,完成整个调制过程。
3 验证与实现
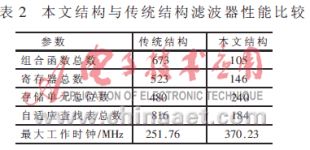
根据以上设计,用Altera公司的StratixII系列器件EP2S30F484C3实现4、16、64、256QAM调制器。将本文的MQAM调制器设计方法和传统方法在硬件资源消耗和最高工作频率等方面进行比较,结果如表2所示。
由表2可以看出,本文结构较之传统结构在硬件资源消耗和最大工作频率方面有较大的改善。
本文讨论了MQAM调制器在FPGA上的一种简化高效的实现方法。其中,主要是系数对称的CSD编码滤波器和简化混频器的设计,使得系统中不需要乘法器,而且实现模块复用。仿真实验表明,该方法可以提高系统的工作频率,而且消耗资源少,是较理想的MQAM调制器设计方法。
参考文献
1 臧道华. 无线信道中信号传输的自适应调制技术. 南京理工大学学报,2001;(12):22~35
2 Yongbin Wu, Shayan, Y.R. ′Implementation of high-peed multi-level QAM modems based on Xilinx Virtex-II FPGA′.Electrical and Computer Engineering, 2003. IEEE CCECE 2003. Canadian Conference on, 2003;1(4~5):195~198
3 Zhangwen Tang, Jie Zhang, Hao Min. A high-speed, pro-grammable, CSD coefficient FIR filter. Consumer Electronics,IEEE Transactions on,2002;48(4):834~837
4 Soderstrand, M.A.′CSD multipliers for FPGA DSP applica-tions′ Circuits and Systems, 2003. ISCAS ′03. Proceedings of the 2003 International Symposium on,2003;5(25~28) V-469~V-472
5 Kei-Yong Khoo, Kwentus, A. Willson, A.N., Jr. A progr-ammable FIR digital filter using CSD coefficients′.Solid-State Circuits, IEEE Journal of,1996;31:(6)869~874
6 孟利民,杨杨,仇佩亮.基于DSP技术的自适应调制器的设计.浙江工业大学学报,2001;29(4):323~327