1 引言
    人作为双足行走生物，是在长期的生物进化过程中形成的。人能够不自觉地保持身体的直立性和平衡性，不论是在静止不动还是在行走过程中。一旦失去平衡，人就会产生相应的动作，使身体保持平衡。例如，在静止时，当人的重心偏向一侧时，就会不自觉地向该侧跨出一脚，以使重心位置落于支撑面内。这里，支撑面定义为两脚之间的面积以及两脚的面积。当重心落于支撑面内时，就不会倾倒。再如，在行走过程中，人的重心不断向前移动，超出了两脚尖的位置，迫使人向前迈出脚，这样才使人的行走成为可能，使人的行走自然流畅。因此，控制机器人重心的位置及重心位置的速度，是机器人保持稳定及产生有效步态的关键。本文就是控制机器人的重心位置，使其落于支撑面内，从而达到了机器人稳定性控制" title="稳定性控制">稳定性控制的目的。机器人的重心可以由安装在机器人脚底的力传感器测知。当重心偏向一侧，这一侧的传感器输出偏大，相反的一侧的力传感器等于零，或趋近于零。本文用感知器" title="感知器">感知器来感知机器人重心位置的变化，当重心超出支撑面时，系统将发出动作指令，使机器人保持稳定。
    本文采用的神经网络" title="神经网络">神经网络感知器(Perception)是最简单的人工神经网络，它是FRosenblatt于1958年提出的具有自学习能力的感知器。在这种人工神经网络中，记忆的信息存储在连接权上，外部刺激通过连接通道自动激活相应的神经元，以达到自动识别的目的。感知器模型如图1所示，通常由感知层S(Sensory)、连接层A(Association)和反应层构成R(Response)。

2 人工神经元感知器的学习算法
    可以用下面的方法训练网络：
        (1)初始化S层至连接层(A层)的连接权矩阵

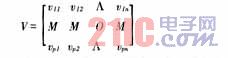
中的各个元素及Ａ层各单元的阀值赋予［－１，＋１］之间的随机值，一般情况下vij＝１θj＝０i＝１，２，Λ，pj＝１，２，Λ，n且在整个学习过程中保持固定不变。
    Ａ层至输出层(R层)的连接权矩阵

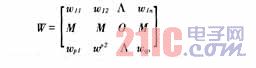
中的各个元素及Ｓ层各单元的阀值θ＝［θ１θ２Λθq］赋予［-1，+1］之间的随机值。
        (2)训练随机选取一输入、输出模式对(Sk,Yk)，这里k=1，2，Λ，m时，网络进行以下步骤的训练。
    第一步，计算连接层各单元的输出

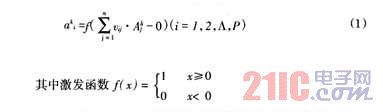
    第二步，以连接层的输出作为输入层的各单元的输入计算输出层的实际输出



    在学习过程中，当所有的m个样本模式对都提供给网络学习一遍后，还需从头再继续提供给网络学习。直到达到最大学习次数，以防止发散或无限震荡，或者满足误差限制。
3 计算机控制系统
    机器人重心位置是由脚底的力传感器测定的。当某一侧的传感器输出值趋于零或小于预定的值时，说明重心已经偏向相反的另一侧，机器人处于危险状态。这时机器人就应该产生一定的动作，向另一侧跨出一脚，以使机器人的重心位于支撑面内。
    整个控制系统如图2所示。

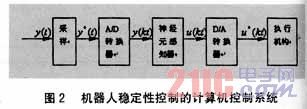
其中，y(t)是传感器输出向量，为模拟量，经采样、Ａ／Ｄ转换后为人工神经网络感知器的输入向量y(kt)。
    本文取感知器的输入层单元与输出层单元的个数相同。感知器经过训练好以后，系统将时实监控机器人的重心位置，当重心偏向某侧，相反侧的力传感器的输入小于设定的安全值时，神经网络相应于该侧的输出为1，其余均为0，系统将根据神经网络的输出，做出相应的动作指令；当传感器的输入均大于设定安全值时，神经网络的输出均为0，系统不产生任何动作指令。
4 仿真
    本文假设在机器人的脚底安装有力传感器，左脚的后部、左部和前部各一个，右脚的前部、右部和后部各一个。依次编号为pi,i=1,2,Λ 6，构成输入向量
    P＝［p１，p2，p3，p4，p5，p6］Ｔ
假设机器人的重是100kgf，当机器人的脚底的传感器输出为2kgf，即认为机器人处于危险状态。设神经网络感知器的输入为

    对应的理想输出为

即认为力传感器的输出为2kgf时机器人处于危险状态，传感器的输出为3kgf时，认为机器人处于安全状态。连接权值和阀值的初始值分别是






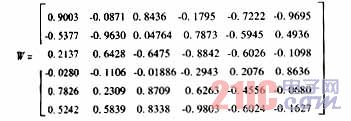
    经过n=1335次迭贷，输出达到期望值。连接权值和阀值分别为




5 结论
    本文就双足行走机器人" title="双足行走机器人">双足行走机器人的稳定性控制提出了一种新的控制方法，它是建立在人工神经网络感知器上。试验表明，该方法简单易行。