一种多级数字混沌编码方案及其硬件实现
2008-10-22
作者:张翌维 柯熙政 席晓莉 毛
摘 要: 以驱动参量法作为同步实现模型,提出一种新的数字混沌通信方案,并对传统混沌加密方法进行了改进。将公钥" title="公钥">公钥与用于编码的私钥分离, 攻击者只能得到公钥,只有权威的接收者才能得到私钥。针对此方案设计了基于ARM处理器的数字混沌通信编解码模块,试验结果证明该方案具有较好的实际意义和应用价值。
关键词: 数字混沌 混沌编码 混沌通信 ARM处理器
随着混沌同步" title="混沌同步">混沌同步手段的不断发展,近些年来,利用混沌同步思想进行保密通信" title="保密通信">保密通信已成为研究热点[1~2]。笔者对基于连续流混沌的模拟通信系统进行了研究,但结果并不满意。混沌同步解调对模拟器件及电路设计要求很高,理想的通信状态难以实现;其次,同步信号的传输占用了较多的信道资源,且易受攻击,降低了保密性[3~4]。目前,离散混沌动力系统用于保密通信,受到了人们的广泛重视。数字混沌通信系统具有较高的保密性,加密方法十分灵活;同步信号与密文信号可复用为单信道,节省了信道资源。特别是DSP处理器及ARM核芯片在通信设备中的使用,为数字保密通信提供了强大的硬件支持,从而使加密算法的设计更加模块化、平台化。
本文提出一种多级数字混沌保密通信方案,以驱动参量法[5] 作为同步实现模型,并进行了改进。将公钥与用于编码的私钥分离;攻击者只能得到公钥,只有权威的接收者才能得到私钥。仿真结果表明,系统具有较好的安全性和稳定性。最后,笔者设计了基于ARM处理器的多级数字混沌通信编解码模块,效果理想,其通信速率和通信质量基本达到数字通信系统的要求。
1 驱动参量同步
近年来,人们提出了许多同步方法,其共同点在于系统之间必须存在耦合作用驱使它们朝相同的状态发展,最终具有相同的动力学行为,达到同步。
已知qn是一个离散混沌序列" title="混沌序列">混沌序列,进行下面的变换:
其中y=(y1,…,yn)为非线性系统的状态变量。在驱动作用下,非线性系统原有的状态发生改变,进入一种更加复杂的混沌态。
随着驱动系数k的增大,参量ξj的变化范围增大;当k超出某一阈值时,即参数ξj的变化范围足够大时,在一个ξj的共同驱动下,两个或多个混沌系统会在新的动力学的基础上达到完全同步。
2 混沌编解码器的设计
图1为较常见的混沌序列编解码通信系统框图。可以看到,这种通信方式必须在接收端产生与发射端时间上同步的混沌同步信号。而同步信号的产生需要另加信道,或者将发送端的混沌信号" title="混沌信号">混沌信号和已调混沌序列以复用的方式发送。这些方法虽然解决了收、发端的同步问题,但是系统的保密性将大打折扣,用于解码的混沌序列直接暴露在信道中,一旦被截获,破译的几率会相当高。
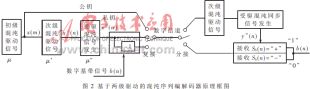
本文采用驱动参量法使接收端与发送端混沌序列同步,为了进一步提高系统的保密性,在系统中加入了两级驱动机制。初级混沌信号用以驱动次级混沌,次级混沌将驱动受驱混沌信号,初级产生的驱动信号与已编码信号以时分复用的方式发送。在此方式下,在信道中传输的并不是用于解码的混沌同步序列(私钥),而是驱动参量(公钥);在接收端解调出初级驱动信号,还原出用于解码的受驱混沌同步信号,从而大大提高系统的保密性。对于非权威的接收者,还原这个加密过程将非常复杂。图2给出了本系统的原理图。
以经典的Logistic映射作为混沌信号发生模型。Logistic映射:
x(n+1)=μ×x(n)×[1-x(n)] (4)
其中0<x(n)<1,0<μ<4。由 Lyapunov指数定义可知,当3.58<μ<4时,该映射是混沌的。
具体过程为:初级混沌驱动信号x(m),以相等的时间间歇Td改变次级混沌的初值x′(mTd+1),在一个时间段内,时间间歇Td=![]() ;次级混沌驱动信号x′(n),以驱动参量法为模型,驱动收、发端受驱混沌信号的参量μ′′,使整个系统达到同步,受驱后产生的混沌同步信号x′′(n)、y′′(n)将参与编、解码。
;次级混沌驱动信号x′(n),以驱动参量法为模型,驱动收、发端受驱混沌信号的参量μ′′,使整个系统达到同步,受驱后产生的混沌同步信号x′′(n)、y′′(n)将参与编、解码。
系统中编码部分采用键控方式,当所发送基带信号为“1”时,受驱混沌信号原样发送;为“0”时,受驱混沌信号取反后发送。在适当地选择系统参数后,从首归映象(如图3(a)所示)可以看出,两级驱动产生的混沌信号具有十分复杂的混沌态,这也正是此方案用于保密通信的一大优势。
设编码后的密文为Sb(n),公钥与密文复接后的信号服从表1数据格式。

为了验证本方案的可实现性,以32位运算精度进行数值模拟,采用定点运算方式。对于Logistic映射,初级混沌μ=3.8906,Td=100;次级混沌μ′=4;驱动参量初值ξj(0)=4,驱动系数k=1.8594;发送端受驱混沌初值x′′(0)=0.4375,接收端初值y′′(0)=0.9625。仿真结果如图3(b)所示,受驱的两路混沌演化至850点后达到同步。
3 系统硬件实现
混沌对初值的敏感性决定了混沌迭代运算必须是高精度的,笔者选用PHLIPS的LPC2200系列ARM7微处理器,构建了32位数字混沌通信试验平台。将正弦信号采样、量化编码后作为基带信号参与键控调制,在500kbps的码元传输速率下,接收端无失真地解调出了基带信号,且收、发端同步性能良好。图4是专为本系统设计的信道监测软界面。
试验结果表明,此方案对通信速率的要求并不苛刻。在32位运算精度下,受驱混沌的同步速度要快于数值模拟时的情形。对几组试验结果分析表明,混沌同步的演化过程控制在200点以内。
另外,信道误码对信号的解调也是有影响的。在一帧信息内,如果公钥部分发生误码,将影响到一帧内的所有位信息,但不会影响到下一帧;如果密文部分发生误码,将只影响到发生误码的位信息,同一帧内的其它位信息不会受到影响。根据以上分析,对于单极性基带信号,可得出解码错误率PI和信道误码率Pe之间的关系:

其中A为基带信号峰值,σn为噪声均方根值。可以看出,在(0,1)内,随着Pe的增大PI亦呈逐渐增长趋势。
本文提出了一种多级数字混沌保密通信方案,结合驱动参量同步方法,着重介绍了系统编解码器的设计与实现。与常规混沌保密通信系统相比,此方案的优越性在于:
(1)将驱动参量与已调信号以数字复用方式发送,使用单信道方式,降低了系统开销;
(2)即便窃听者获取了驱动参量(公钥)和已调信号(密文),在不知道受驱机制的情况下,根本无法还原出用于解调的混沌序列(私钥);
(3)驱动参量与已调信号复用,在一帧数据中既有密文信息又有用于解密的驱动信号,从而达到一种编码同步,避免了时域混沌同步实现的复杂性。
在硬件资源允许的情况下,可以增加混沌驱动的层次性,提升系统复杂度,进一步提高系统保密性。
参考文献
1 Pecora L M, Carroll T L. Synchronization in chaotic system[J].Phys Rev Lett,1990;64(8):821~824
2 Frey D. Chaotic digital encoding: An approach to secure commuciation[J]. IEEE Transactions on Circuits and Systems-II, 1993; 40(10): 660~666
3 Chua L O. Chua′s circuit: ten years later[J]. IEICE Trans. Fundamentals,1994; E77—A(1):1811~1821
4 Sharma N. Exploring synchronization to combat channel dis-tortions in communication with chaotic system[J]. Int. J.Bifurcation and Chaos,2000;10(4):777~785
5 杨世平,牛海燕,田 钢等. 用驱动参量法实现混沌系统的同步[J]. 物理学报, 2001;50(4):619~623
6 Werter M J.An improved chaotic digital encoder[J]. IEEE Transactions on Circuits and Systems-II,1998;45(2):227~229
7 Yang T,Chua L O. Error Performance of chaotic digital codedivision multiple access(CDMA) systems[J].Int J Bifurcation and Chaos,1998;8(10):2047~2059
8 Kolumban G,Kennedy M P, Chua L O.Role of synchronization in digital communications using chaos-part II:chaotic modu-lation and chaotic synchronization[J]. IEEE Transactions on Circuits and Systems I.1997; 44(14): 1129~1141
9 HASLER M.Synchronization of chaotic systems and transmis-sion of information[J]. Int J Bifurcation and Chaos, 1998;8(3): 639~644