椭圆曲线密码体制(ECC)作为新一代公钥技术的典型代表，提供了更好的算法实现性能、更高的安全性和更低的实现代价[1]，同时能够完成数据加密和数字签名的功能。
    现场可编程逻辑门阵列(FPGA)是一种基于4输入查找表(LUT)、通过可编程互联连接的可配置逻辑块(CLB)矩阵的可编程半导体器件。与为特殊设计而定制的专用集成电路(ASIC)相对，FPGA可以针对所需的应用或功能要求进行编程。其逻辑资源远比一般处理器多，而且具有编程方便、集成度高、速度快的特点。目前以硬件描述语言（VHDL或Verilog HDL）所完成的电路设计，可以经过简单的综合与布局，快速下载至FPGA上进行测试，因而被称作是现代IC设计验证的主流技术。
    目前，ECC的实现方案主要有软件和硬件两种，其中硬件实现方案因具有运算速度快、带宽要求低等优势，被广泛应用于硬件加密设备和无线网络通信等领域。
    FPGA芯片在执行加密过程中，会有消耗能量的晶体管充放电过程。功耗分析时，依赖于硬件的各种加密操作与功耗具有相关性，其原理是通过监测硬件在加密过程中产生的功耗曲线，利用统计学和攻击者的经验对收集到的信息进行分析，从而获得加密过程的相关数据[2]。
    本文采用NIST定义在有限域GF(2m)上的Koblitz曲线：y2+xy=x3+x2+1。建立在该曲线上的椭圆曲线点乘运算可以快速实现，因此特别适合构建高效的密码系统。

    ECC的安全性主要依赖于椭圆曲线离散对数问题（ECDLP）的难解性。ECDLP的定义如下：若P是椭圆曲线E上的一点(称为基点)，P的阶为素数n，k为一随机选择的正整数，已知Q=kP，无法求得或者很难求得k，把Q定义为公钥，k为私钥。
    在椭圆曲线上建立公钥密码系统的过程中，其核心计算是点乘运算，因此对椭圆曲线点乘算法进行深入研究很有必要。
    ECC的层次结构由自上而下可分解为加解密层、群运算层、域运算层，如图1所示。各个运算模块通过状态机的合理控制，实现FPGA上椭圆曲线点乘算法。

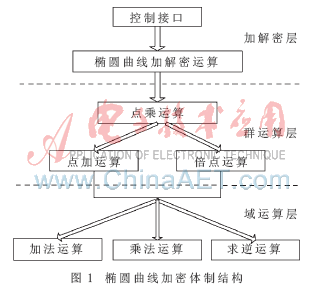
    随着计算资源的急剧膨胀，特别是边信道攻击等新型的密码攻击方式的出现[5]，给ECC的安全性带来一定的挑战。针对ECC边信道分析攻击，采取的防御手段既有在算法实现方法上改进的软件手段，也有通过增加噪声干扰和采用数模混合电路产生真随机数来扰乱掩码和时钟的硬件手段[6]。
1.2 实现方案
    在FPGA上实现各种密码算法的过程中，应考虑到FPGA的既定芯片资源限制以及如何在更少的资源量和更快的时序中找到平衡点这两个因素。
    由于1个求解逆元的操作在计算时间上约和70个乘法器相近[7]，因此在实施ECC的点乘算法时，应尽量减少使用求逆运算。
    在设计与实现椭圆曲线的点乘算法时，本文内容主要将作如下安排。首先，从算法级别对乘法器运算单元进行改进，以提高乘法器的速度。然后，对乘法器模块由混合结构乘法器实现的点乘运算进行性能评估。最后，在经典椭圆曲线点乘算法的实现过程中，通过使用乘法器代替模平方运算的方法来增加计算的隐蔽性，算法内部实现逻辑的改善，达到提高算法安全性的目的。
2 乘法器模块设计
    有限域上的乘法器是点加运算和点乘运算所要涉及的核心运算。实现多项式乘法器最基本方法是移位相加，而移位操作在FPGA中实现非常方便，不需要使用任何逻辑单元。研究表明，根据FPGA的特点而设计的乘法器具有明显的速度优势。
    本文使用的StratixⅡ系列器件是ALTERA公司基于1.2 V工艺的现场可编程门阵列。选用拥有高达72 768个ALUTs、903个IO资源的EP2S90F1508C3芯片作为乘法器实现方案的硬件基础，如图2。

    图2中，A、B分别表示多项式乘法器的乘数与被乘数，F表示有限域GF(2m)的多项式基，CLK为主时钟信号，reset为复位信号，start为使能信号，result和done分别表示乘法器的运算结果和运算结束标志。
    将混合结构乘法器[8]与目前点乘算法所使用的乘法器做包括资源占用和计算性能两方面比较。乘法器1是使用文献[8]中提到的乘法器实现的椭圆曲线点乘算法在EP2S90F1508C3芯片上的实现，乘法器2是目前点乘算法所使用的乘法器。
    通过使用Synplify Pro 9.6对2种乘法器进行综合以及ModelSim-Altera的前仿真，文献[8]使用23个时钟数、算法2使用107个时钟周期所得到的资源和计算性能评估结果如表1和表2所示。

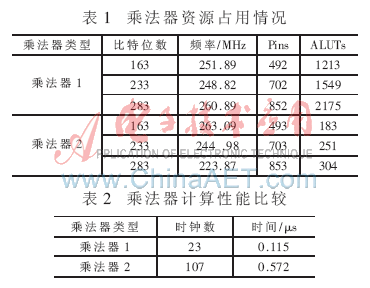
    在200 MHz的时钟频率下，乘法器计算性能的评估结果如表2所示。
    混合结构乘法器的计算性能较目前使用的乘法器2的性能有显著的提高。
    为验证乘法器计算正确性，以163 bit的乘法器为例，其仿真结果如图3所示。

    下面将在目标芯片上实现基于这两种乘法器的点乘算法。
3 椭圆曲线点乘算法的FPGA实现
    计算有限域GF(2m)点乘kP的最直接方法是使用倍点和点加相结合的double-and-add方法。如果ki=0，则仅执行倍点计算；如果ki=1，则执行倍点计算和点加计算。Double-and-add算法需要(m-1)次倍点运算和m/2次点加运算[12]，而使用非相邻（NAF）编码思想的二进制点乘算法可以将计算点加的平均次数减少至m/3[9]。
    基于上述两种乘法器模块，本文实现的是使用NAF编码的163 bit二进制域上的椭圆曲线点乘算法。
3.1 基于NAF思想的椭圆曲线点乘
    使用NAF编码思想计算椭圆曲线点乘是因为椭圆曲线上点的减法和点的加法一样有效，NAF编码可以在不使用椭圆曲线倍点计算的环境下实现点乘运算而仅使用点加和基本的域运算的状态下来完成二进制域上的点乘操作。
    在计算NAF编码的二进制点乘算法时，首先需要知道如何计算给定数的NAF值，然后使用该算法的思想完成椭圆曲线的点乘kP计算。其算法描述如下：
 

其中，m表示运算比特位数，f(z)是有限域GF(2m)的多项式基，n是基点G的阶，x和y分别表示的是基点G的横坐标和纵坐标。
    在使用工具Synplify Pro 9.6综合后，混合结构乘法器的点乘运算和基于原有乘法器的点乘算法相比，在计算性能和资源占用等性能上的评估结果如表4所示。

    设计实现的基于混合结构乘法器的点乘算法（点乘算法1）在完成一次点乘运算的时间上较原有的点乘算法有所提高，且在资源占用上较原有算法有所减少，与同类型的点乘算法相比在计算性能上有明显提高。
4 算法安全性
    基于Montgomery Ladder的椭圆曲线多倍点运算是不安全的[10]。为了增加算法的抗功耗分析能力，通常的做法是采用增加计算的隐蔽性等软件手段或者引入噪声干扰以及掩膜方式等硬件手段[6]。
    本文通过改进椭圆曲线点乘算法中的内部结构可以做到提高算法的抗功耗分析能力，其中使用乘法器替代模平方算法能有效防范边信道攻击[11]。本文以经典椭圆曲线点乘算法为例(算法1)，从计算安全的角度考虑，使用乘法器替代模平方算法的方法和VHDL语言在 EP2S90F1508C3芯片中(算法2)实现。
    在使用综合工具Synplify Pro 9.6对经典的点乘算法1和算法2进行综合后，在50 MHz的时钟频率下，两种点乘算法分别在9.6 ms和10.1 ms内完成一次点乘操作。可见，为了让经典椭圆曲线点乘算法获得更好的抗功耗能力，而使用乘法器替代模平方算法的改进措施对点乘算法的计算性能没有明显改变。
    通过对实现基于混合结构乘法器的点乘算法仿真验证，结果表明，基于混合结构乘法器的点乘算法在运算速度上较改进前有一定的提高，和同类型的椭圆曲线点乘算法比较有显著提高。与此同时，为提高算法的抗功耗分析能力，使用模乘运算取代模平方运算的改进措施，对点乘算法的执行时间影响较小。
参考文献
[1] CHOI Y，KIM H W，KIM M S.Implementation of elliptic  curve cryptographic over GF(2163) for ECC protocols[S].2001.
[2] DANIEL M G.A survey of fast exponentiation methods[J]. 1998，27.
[3] IEEE P1363/D13.Standard specification for public-key cryptography[C].1999(12).
[4] 王建，蒋安平，盛世敏.椭圆曲线加密体制的双有限域算法及其FPGA实现[J].北京大学学报，2008，44(6)：871-875.
[5] AIGNER M，OSWALD E.Power analysis tutorial[C].Institute for Applied Information Processing and Communication University of Technology Graz，2000.
[6] 郑新建，张翌维，沈绪榜.SPA和DPA攻击与防御技术新进展[J].小型微型计算机系统，2009(4).
[7] 汪朝晖，陈建华.素域上椭圆曲线密码的高效实现[J].武汉大学学报（理工版），2004，50(3).
[8] 高献伟，靳济方，方勇，等.GF（2m）域乘法器的快速设计及FPGA实现[J].计算机工程与应用，2004(25).
[9] JOY M，TYMEN C.Compact encoding of Non-adjacent  forms with applications to elliptic curve cryptography[J].  Public Key Cryptography，LNCS 1992，Springer，pp.353-364，2001.
[10] 赵彦光，白国强，陈弘毅.一种针对特征2域椭圆曲线密码芯片的差分功耗分析[J].微电子学与计算机，2006，23(12).
[11] 余荣威，陈建华.抗侧信道攻击的椭圆曲线点乘算法设计[J].计算机工程与应用，2006.