摘 要:提出用神经网络控制器实现大偏差范围内的解耦控制,由PID控制实现小偏差时的快速稳定并消除静差。这种复合控制方法应用于UPFC的动力学模型收到了良好的效果。
关键词:UPFC;BP网络;解耦控制 TM761;TM743;TP2733
0 引 言
在UPFC 应用研究中普遍使用了UPFC的输出模型。众所周知,UPFC的输出模型只是稳态下的等效电路。它不反映UPFC的动力学性质。凡是基于UPFC输出模型 的应用研究都忽略了UPFC的内部运动过程,这显然不够精确,或者说以这种研究方法认识UPFC带有很大局限性。文献[1]提出的UPFC建模方法所建模 型是动力学模型。从控制工程的角度看,UPFC装置本身是一个较为复杂的非线性动力学系统,研究其控制方法对装置开发和应用都非常必要。
1 UPFC的主电路及其动力学模型
1.1 UPFC的主电路
为了讨论问题方便采用图1所示主电路结构(实际电路结构可能考虑到降低谐波含量而采用多重化技术,但原理相同。)
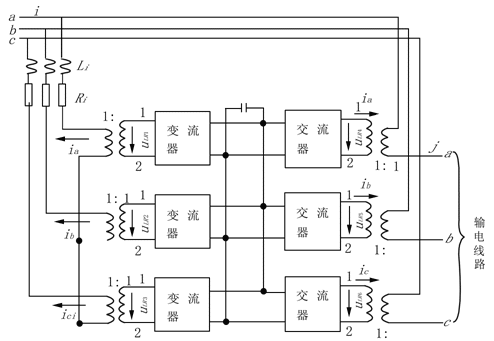
图1 UPFC主电路简图
1.2 UPFC的动力学模型
串联支路的回路方程:
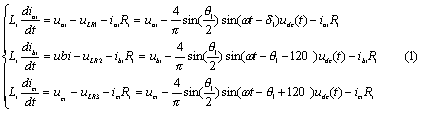 |
并联支路的回路方程
|
|
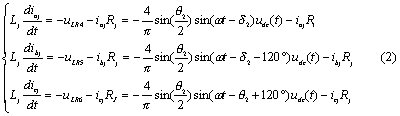 |
||
式中的Lj、Rj是根据戴维南定理得出的串联变压器输出阻抗(注意:Lj、Rj在图1中没有标出)。另一方面,再由能量守恒可知,直流侧电容的充放电过程决定于UPFC两侧有功的不平衡性,有:
|
|
|
|
|||
|
|
|
|
|
式(1)、(2)、(3)、(4)构成了UPFC装置的动力学模型。
2 UPFC的控制回路
UPFC装置本身包括三个控制回路,在这三个回路基础上增加网络方程和发电机方程即可得到含UPFC的系统数学模型(注:本文只研究UPFC装置内部三个基本控制回路,若还要关注系统,只需在此基础上增加相应方程)。
由图2可见(见下页),UPFC装置的控制系统包括三个控制回路。控制回路1的作用是实时补偿输电线路无功功率(标幺制下的无功电流Iq);控制回路2的作用是维持直流连接电容电压Udc恒定;控制回路3的作用是调节串联变压器输出电压V。不难看出,控制回路2与另外两个控制回路存在耦合作用。因此,若三个控制回路均采用PID控制逻辑很难得到满意的控制效果。作者设计的神经网络(ANN)与PID的复合控制规律取得了良好的效果。
3 ANN-PID复合控制器设计
3.1 神经网络控制概述
从控制的观点,可以把神经网络看作一个具有m 维向量输入和n维向量输出的非线性动力学系统,并通过一组状态方程和一组学习方程加以描述。状态方程描述每个神经元的兴奋或抑制水平与它的输入及输出通道 上的联结强度间的函数关系,而学习方程描述通道的联结强度应该不断地修正。神经网络就是通过修正这些联结强度进行学习,从而调整整个网络的输入输出关系。
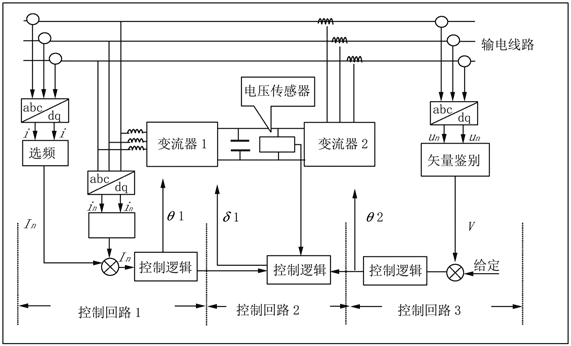
图2 UPFC的三个控制回路
|
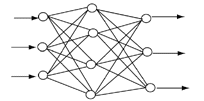
3.2 神经网络控制器设计及训练样本获取 我们使用BP网络及其误差反传学习算法,网络结构如图3所示: 在确定网络结构和学习算法以后,可以开始对网络进行离线训练。训练之前的样本获取是一项十分重要的工作。它决定了训练后的网络性能。样本获取的途径 因控制对象的不同而异本文的控制对象已给出确定的动力学模型。通常,对于有确定数学模型的控制对象并不适合采用人工神经网络控制。原因在于基 |
图3 BP神经网络结构 |
于精确数学模型的控制规律设计理论已相当成熟且应用广泛。但是,本文的控制对象具有多回路、强耦合、非线性的特点。作者曾采用PID控制,虽然也能使三个回路达到稳定,但由于耦合作用的存在和PID算法的局限性,导致了较大的超调量和较长的过渡过程。
PID控制性能差的原因在于暂态过程是一个“边解耦,边控制”的过程,而且PID的固有缺陷使它难以兼顾快速性和稳定性。这里使用BP神经网络主要目的是避开解耦过程,利用BP网络的非线性映射功能直接得出三个回路的控制量。训练样本获取方案如下:
![]()
输入矢量的形成:系统共三个回路,即三个被控量Q、V、Udc。输入矢量由被控量的偏差划分为七个档次经排列组合而得到。因此,输入矢量总数
目标矢量的形成:系统控制量分别为θ1、θ2、δ1。给定一个输入矢量(ΔQiΔViΔUdci),通过PID算法可以得到稳态输出(θ1i、θ2i、δ1i),这个稳态下的输出即为相应的目标矢量。作者采用这种方法获取目标矢量的主要原因是可以借助控制系统的仿真软件(MATLAB)方便地得到。
3.3 ANN-PID复合控制
利用BP 网络的映射功能形成控制量,虽然避开了多回路解耦过程,但由于是开环控制无法消除稳态误差。众所周知,PID控制用于小偏差线性系统时具有明显的优势。于 是,本文设计了ANN-PID复合控制的方法,即在大偏差范围内投入神经网络控制器,小偏差范围内切换到PID控制器。两个控制器的切换通过编程是很容易 实现的。
4 仿真研究
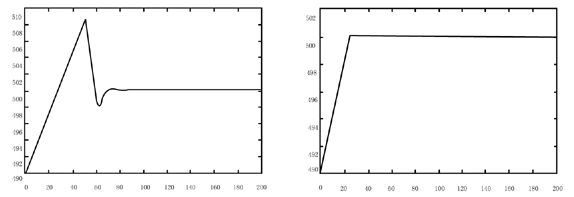
图4-1 回路2的PID控制 图4-2 回路2的ANN-PID复合控制
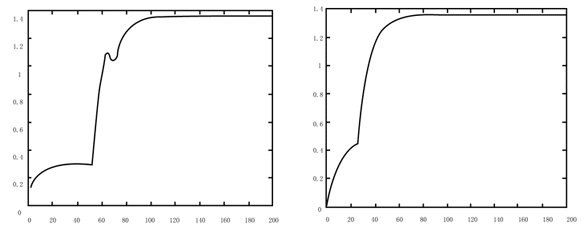
图4-3 回路1的PID控制 图4-4 回路1的ANN-PID复合控制
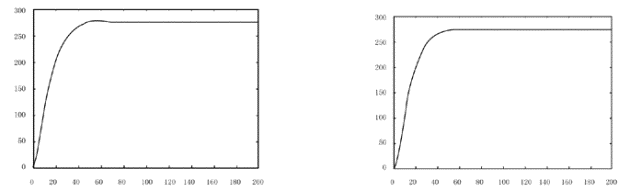
图4-5 回路3的PID控制 图4-6 回路3的ANN-PID复合控制
由仿真结果可以看出,单独使用PID控制时回路间的耦合作用使动态响应曲线有超调和多个极点导致了快速性、稳定性较差;ANN-PID复合控制则表现出良好的解耦控制效果,三个控制回路的动态性能都有显著改善。