1980年4月Anderson第一次阐述了入侵检测的概念，指出可以使用审计网络数据的方式判断非法入侵的发生[1]。在网络数据的审计中，没有一种确定的函数关系可以鉴别非法入侵。因此引入机器学习的方法，作为入侵行为和网络数据特征之间模型进行函数逼近。
    机器学习的方法在入侵检测领域应用广泛，并有较好的检测效果。传统的机器学习算法需要大量的网络数据，而正常的网络数据特征有着小样本、高维数、多变性的特点。支持向量机（SVM）对小样本、高维数的数据有着较好的训练能力，已经被应用于入侵检测[2]。最小二乘向量机（LSSVM）是SVM中的一种，相比SVM有着更快的运行速度。LSSVM惩罚因子C和核函数参数?滓的选择使用网格搜索，耗时且分类精度不高。而粒子群优化（PSO）算法的寻优求解能力较为突出，可以利用PSO算法对LSSVM的相应参数进行选择[3]。
　PSO算法中一个重要的参数就是惯性权重w。w较大时,全局搜索能力较强;w较小时,局部搜索能力较强。基本PSO算法采用固定w，搜索的性能和效率不高。参考文献[4]提出了让w随着进化的进行而线性减少的策略，相应的PSO算法称为线性权重下降PSO(LWDPSO)算法。该PSO算法在提高搜索效率的同时有着早熟收敛、陷于局部最优的缺点。本文提出一种改进的PSO算法，即并行PSO算法。该算法将粒子群分成两组[5]进行协同搜索，两组粒子具有不同的w，其中w较大的粒子组侧重全局搜索；w较小的粒子组侧重在w大的粒子组找到全局最优位置的附近区域进行精细搜索。每组都有一部分固定的粒子，其余的粒子根据进化阶段动态分配给两组，通过动态分配粒子保证算法初期以全局搜索为主，后期以局部搜索为主。通过适应度函数的仿真实验，证明了并行PSO算法的寻优性能更优。


    选用RBF函数作为核函数:

2  PSO算法
    PSO算法源于对鸟类觅食行为的模拟，通过鸟群之间的集体协作使群体达到最优。标准PSO算法初始化产生一群粒子,每个粒子以一定的速度在n维空间里飞行，飞行速度由个体的飞行经历和群体的飞行经历动态调整。X1=(Xi1,Xi2,…,Xin)是粒子i当前的位置，V1=(Vi1,Vi2,…,Vin)是粒子当前的速度，P1=(Pi1,Pi2,…,Pin)是粒子i所经历过的最好位置,在这个位置粒子i拥有最佳适应度。设f(x)为最小化的目标函数，则粒子i的最好位置由下

3 改进PSO算法
　粒子群进化前期应该以全局搜索为主，搜索整个空间，但不能放弃局部搜索，因为全局搜索的粒子速度较快，发现的位置的范围虽然广泛，但精度不高，容易错过全局最优位置；进化后期应该以局部搜索为主，但不能放弃全局搜索，因为局部搜索虽然精细，但搜索的范围较小，无法搜索到较远的更优位置。
　本文提出一种改进PSO算法，即并行PSO算法。设粒子的数量为S，总进化代数为G，当前进化代数为i。该算法将粒子群分成两组，运行PSO算法时惯性权重w分别设置为0.95和0.4，其中w为0.95的粒子组侧重全局搜索，w为0.4的粒子组侧重在w为0.95的粒子组找到全局最优位置的区域进行精细搜索。每组粒子都有一定基本的粒子数量，均为S/4。剩余S/2粒子根据进化阶段动态分配给两组，分配给w为0.95的粒子组为S×(G-i)/2G(朝负无穷方向取整);分配给w为0.4的粒子组为S×i)/2G(朝正无穷方向取整)。
　进化初始，w为0.95的粒子组粒子数目最多，达到3S/4，进行全局搜索，余下的S/4 w为0.4的粒子组对全局搜索到的当前最优位置的小范围区域进行局部搜索，期望在该区域中搜索到更优位置；进化后期，动态粒子逐渐从w为0.95的粒子组调整到w为0.4的粒子组，空间已被w为0.95的粒子组多次搜索，w为0.4的粒子组针对当前最优位置的相关小范围区域进行局部搜索，w为0.95的粒子组在对空间中当前全局最优位置的相关大范围区域进行搜索，不放弃任何寻找到全局最优位置的机会。
4 仿真实验及分析
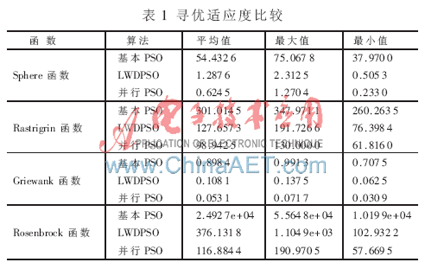
     使用四种典型的测试函数[6]: Sphere函数、 Rastrigrin函数、Rosenbrock函数和Griewank函数作为适应度函数进行测试。各算法最大进化代数为500代，种群规模为80,优化方程的维数为30,c1、c2等于2，搜索的空间为[-100,100]。为避免实验中偶然性现象，现将PSO三种算法针对这四种函数同时进行了10次实验。图1~图4分别是四种测试函数对三种算法的适应度变化与进化代数比较曲线图。表1是三种算法在10次实验次数中取得的适应度的平均值、最大值和最小值。

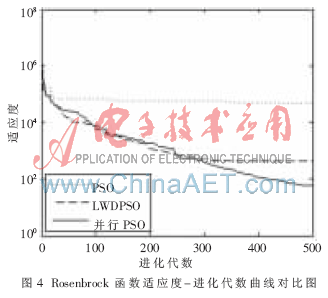
    基本PSO算法粒子一直进行全局搜索，没有进行局部精细搜索，因此无法找到较优位置，适应度值一直较大,寻优效果较差；LWDPSO算法在前期有较好的搜索效果，但是在中后期收敛之后对最优位置的搜索没有任何突破，早熟的迹象非常明显；并行PSO算法有着较好的全局搜索能力以及局部收敛能力，对最优位置的搜索较为稳定，避免了局部最优，没有早熟的缺点，同时搜索到了最优位置。同时从表1可以得出：基本PSO算法的寻优较差，得到的适应度远远高于其他两种算法；LWDPSO算法的寻优结果优于基本PSO算法，次于并行PSO算法；并行PSO算法的寻优结果优于基本PSO算法和LWDPSO算法，实验得到的适应度平均值、最大值和最小值在三种算法中都是最低的。

5 基于并行PSO算法的LSSVM建模方法
    将LSSVM的惩罚因子C和δ核参数映射成粒子，根据并行PSO算法进行优化选择，最终使得建立的模型估计值与期望值的逼近程度达到预期目标。其算法流程如下：
    (1) 并行PSO算法参数初始化,将粒子群分成两组，惯性权重w分别设置为0.95和0.4。
    (2) 根据设定的适应度函数，计算每个粒子的位置。
    (3) 将粒子的位置与自身最优位置进行比较,如果当前位置相应适应度小，则更新自身最优位置。
    (4)比较每个粒子的自身最优位置适应度求出全局最优位置。
    (5) 根据当前进化代数动态调整两组粒子的数目，进行下一代进化。
    (6) 所有进化次数结束，将此时全局最优粒子分别映射为惩罚因子C和核参数?滓,并以此为优化结果，建立模型。
6  实验过程及结果
6.1实验数据预处理
    实验中采用的数据取自1999年DARPA为KDD竞赛提供的一个异常检测的标准数据集，它是由美国麻省理工学院的Liconln实验室通过模拟一个典型的美国空军网络而获得原始的TCP/IP网络通信数据,对于每一个TCP/IP连接，提取了41个属性。数据中有四种类型的攻击：未经授权的远程访问(R2L)、拒绝服务攻击(DoS)、对本地超级用户的非法访问(U2R)和扫描与探测(Probing)。标识为正常的数据占19.6%,攻击数据占80.4%。
　实验中的训练数据取自于原始数据集中kddcup数据，测试数据取自于corrected数据,训练数据和测试数据采用等间隔的选取方式。测试数据共选取54 220条，其中正常数据12 140条、攻击数据42 080条,训练数据共33 520条,按类型和间隔平均分成10组，分别使用10组训练数据建立模型对测试数据进行测试，实验结果取10次实验的平均值。
　实验中,需要对数据进行处理，实验数据的protocol-type、sevice和flag属性使用字符串表示,对其进行数字替换处理，对属性中不同的类型使用不同的数字表示。另外，必须要对所有属性进行归一化处理，公式为：
  

其中new为归一化后的数据，old为归一化前数据，max为属性的最大值，min为属性的最小值。
6.2 实验结果
    网格搜索、LWDPSO算法和并行PSO算法分别对LSSVM的参数寻优，并建立各自的模型，对测试数据集进行了检测。实验结果如表2所示。

　从表2可以得出，由于训练数据和测试数据采自不同的数据集，网格搜索和LWDPSO算法的检测率较低，误报率和漏报率较高；采用并行PSO算法对LSSVM进行参数寻优所建立的入侵检测模型检测率、误报率和漏报率都优于其他两种算法参数寻优后所建立的模型。
   本文给出并分析了基本PSO算法和LWDPSO算法的定义及特点。提出并行PSO算法,将粒子群分成两组，分别设置不同的惯性权重，惯性权重大的粒子组侧重全局搜索，惯性权重小的粒子组侧重在惯性权重大的粒子组找到全局最优位置的附近区域进行精细搜索。根据进化代数动态调整两组中进化的粒子数，并给出了每组粒子的数量调整公式。通过四个适应度函数仿真实验，证明了并行PSO算法的寻优性能优于基本PSO算法与LWDPSO算法。通过入侵检测实验测试，并行PSO算法对LSSVM参数寻优后建立的模型可以有效提高入侵检测的性能指标。
参考文献
[1]  ANDERSON J P. Computer sercurity threat monitoring and     surveillance[R]. James PAnderson Co, Fort Washington,  Pennsylvania, Aprial 1980.
[2]  MUKKAMALA S, JANOSKIG I, SUNGA H. Intrusion detection using neural networks and support vector machines[C]. Proc of IEEE International Joint Conference on Neural Networks. Washington DC:IEEE Computer Society,  2002: 1702-1707.
[3]  陈光英,张千里,李星. 特征选择和SVM训练模型的联合优化[J]. 清华大学学报(自然科学版),2004,44(1);9-12.
[4]  SHI Y, EBERHART R. A modified particle swarm optimizer[C]. IEEE World Congress on Computational Intelligence. Piscataway:IEEE Press,1998:69-73.
[5]  龙文，梁昔明，肖金红，等.一种动态分级的混合粒子群优化算法[J].控制与决策.2009,24(6):1406-1411.
[6]  CLERC M, KENNEDY J. The particle swarm: explosion, stability, and convergence in multi-dimension complex space[J]. IEEE Transactions on Evolutionary Computation,  2002,16(1):58-73.