一、引　　言

随着计算机技术的进步，有限时域差分方法(FDTD-Finite Difference Time Domain)可以研究的微波电路的越来越广泛，从无源电路到有源电路，从线性电路到非线性电路，从准TEM系统到色散系统，FDTD都已得到了成功的应用.

但是，当电路的几何结构比较复杂，电路电尺寸较大时，不论是其所占用的计算机内存还是所需要的计算时间都是非常巨大的，甚至 在一些情况下即使耗费了计算时间还无法得到需要的精度.例如，在分析波导膜片滤波器时，为正确模拟全部膜片的几何结构，FDTD栅网的网格尺寸选得非常小，从而导致描述整个波导滤波器的网格数量非常大.由于每两个膜片之间都是均匀波导传输线，使用与膜片相同的栅网显然是不必要的.人们曾使用非均匀FDTD栅网的办法解决这个问题，当栅网的大小相差比较大时，不但收敛性不易控制，而且仍无法确保节省计算时间.将Diakoptics思想运用于微波电路的全波分析，通过将电路分割为若干独立的部分，根据每部分的具体结构采用不同的网格，独立地对各个部分进行全波时域分析，由于每部分的网格是均匀的，因而容易保证算法的收敛性.

二、Diakoptics的概念

Diakoptics定义为：将一个电路分解为若干个较为简单的子电路，独立计算子电路的特性，通过连接条件将子电路耦合连接.线性电路理论中子电路的特性用冲击响应函数表示；子电路间的耦合通过串行和并行两种算法完成.串行算法是从电路首尾中的任一端开始向另一端连接，依次将从参考面看入的子电路视为前一级子电路的负载，求出等效的子电路的输入特性，并将此输入特性看成更前一级子电路的负载…，串行算法思路比较简单，易于编写计算机程序，但存在的问题是：当电路中某一个子电路需要调整时，在该子电路之后连接的部分都要从新连接，而且所有的连接计算在时间及空间上只能顺序进行，计算效率较低；并行算法可以从电路中的任何位置开始，同时计算若干个彼此相邻的子电路的连接，且对某个子电路特性的调整并不影响其它子电路的连接，特别是当某个子电路的特性需要反复调整时，对其余子电路的连接计算只需进行一次.

研究微波电路问题时，若微波电路可以被等效为一个线性网络的话，则可以设想描述微波电路特性的格林函数可对应于电路理论中的冲击响应函数.从电磁场理论角度看，时域格林函数g(r，t;r0,t0)为位于r0点的点源t0时刻施加的单位冲击信号在观察点r及t时刻的场，且满足方程

　　(1)

两个微波子电路连接时，其连接参考面上存在着复杂的耦合关系，这种耦合关系可以用电磁波在存在两个不连续界面的媒质中反射和透射现象来形象描述，如图1所示.那么如何将Diakoptics算法应用于微波电路特性分析中呢?在介绍这一点之前，本文首先简要介绍Diakoptics算法的数学描述.

图1　媒质中反射和透射现象可以用来形象描述两个微波子电路间的耦合关系

三、Diakoptics算法的数学描述

以两个二端口网络的串、并行连接给出Diakoptics算法的数学描述.图2假设两个子电路的反射及透射波的冲击响应函数分别为：gr1(t),gr2(t),gt1(t),gt2(t)和hr1(t),hr2(t),ht1(t),ht2(t),上标“r”表示反射波，“t”表示传输波，下标1表示从输入参考面对电路作激励，下标2表示从输出参考面对电路作激励.设f为两个子电路连接后电路的冲击响应函数.使用串行算法，从f网络输入参考面看入的冲击响应为：

fr1(t)=gr1(t)+gt2(t)*hr1(t)*gt1(t)+gt2(t)*hr1(t)
*gr2(t)*hr1(t)*gt1(t)+…+gt2(t)*(hr1(t)
*gr2(t))n*hr1(t)*gt1(t)+…;　(2)

使用并行算法，从f电路的输入端口看入的冲击响应函数fr1(t),ft2(t)以及从f电路的输出端口看入的冲击响应函数fr2(t),ft1(t)分别为：

fr1(t)=gr1(t)+gt2(t)*hr1(t)*gt1(t)+gt2(t)*hr1(t)
*gr2(t)*hr1(t)*gt1(t)+…+gt2(t)*(hr1(t)
*gr2(t))n*hr1(t)*gt1(t)+…
ft2(t)=gt2(t)*hr2(t)+gt2(t)*hr1(t)*gr2(t)*ht2(t)+…
+gr2(t)*(hr1(t)*gr2(t))n*hr2(t)+…　(3)
fr2(t)=hr2(t)+ht1(t)*gr2(t)*ht2(t)+ht1(t)*gr2(t)
*hr1(t)*gt2(t)*ht2(t)+…+ht1(t)*(gr2(t)
*hr1(t))n*gr2(t)*ht2(t)+…
ft1(t)=ht1(t)*gt1(t)+ht1(t)*gr2(t)*hr1(t)*gt1(t)+…
+ht1(t)*(gr2(t)*hr1(t))n*gr1(t)+…

其中，*代表时域卷积，上下标的含义不变.

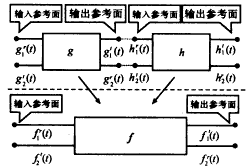
图2　可说明Diakoptics算法的两个子电路连接示意图

多端口子电路连接时，上述算法依然成立，只是式中各冲击函数应换为相应的子矩阵.例如设g网络为输入端有M个、输出端有N个端口的M+N端口网络，h网络为输入端有N个、输出端有L个端口的N+L端口网络(g与h相邻面的端口数目应相同)，g网络输入参考面处的反射、传输子矩阵分别为：

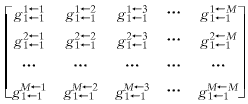
和

式中下标代表参考面，i←j的意思为：i为响应所在参考面，j为激励所在参考面；上标代表端口，m←n的意思为：n为输入端口，m为输出端口.同理,g网络输出参考面处的反射、传输子矩阵分别为：

和

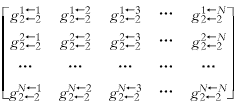
h网络相应子矩阵可用同样方法求得.连接后网络的冲击响应函数［f］为：

［fr1(t)］=［gr1(t)］+［gt2(t)］*［hr1(t)］*［gt1(t)］+［gt2(t)］
*［hr1(t)］*［gr2(t)］*［hr1(t)］*［gt1(t)］+…
［ft2(t)］=［gt2(t)］*［ht2(t)］+［gt2(t)］*［hr1(t)］*［gr2(t)］*［ht2(t)］+…
［fr2(t)］=［hr2(t)］+［ht1(t)］*［gr2(t)］*［ht2(t)］+［ht1(t)］
*［gr2(t)］*［hr1(t)］*［gr2(t)］*［ht2(t)］+…
［ft1(t)］=［ht1(t)］*［gt1(t)］+［ht1(t)］*［gr2(t)］*［hr1(t)］*［gt1(t)］+…　(4)

其中［fr1(t)］、［ft1(t)］、［fr2(t)］和［ft2(t)］分别为M×M、L×M、L×L和M×L阶子矩阵.下面以［gt2(t)］*［ht2(t)］为例说明如何计算矩阵卷积，并以［gt2(t)］*［ht2(t)］的第一个元素为例，说明其物理意义：

　(5)

g1←11←2*h1←11←2：h子网络输出参考面上第一个端口的输入通过gh连接面第1个端口的耦合在g子网络输入参考面上端口1产生的输出；g1←21←2*h2←11←2:h子网络输出参考面上第一个端口的输入通过gh交界面第2个端口的耦合在g子网络输入参考面上端口1产生的输出；g1←N1←2*hN←11←2：h子网络输出参考面上第一个端口的输入通过gh交界面第N个端口的耦合，在g子网络输入参考面上端口1产生的输出；所以［gt2(t)］*［ht2(t)］的第一个元素描述了h网络输出参考面上第一个端口上的输入耦合到g网络输入参考面第一个端口的输出.

四、Diakoptics算法在微波电路分析中的实现

Diakoptics源于网络理论，为将其应用于微波电路的分析中，首先需要建立适于使用Diakoptics方法的微波电路的等效电路模型.

1.微波电路的等效时域网络模型

建立微波电路等效时域网络模型的基本方法是：利用基函数技术(或称时域模技术)将参考面处的场表示为选定的正交基函数的线性组合，将一个微波网络等效为一个多模电路，进而再将多模电路等效为多端口网络的方法.

选定的基函数满足下述条件：只是空间坐标的函数；与时间无关；构成一个完备正交集.且对于给定的微波电路，选定的基函数应能够有效地描述电路中电磁场的分布规律.假设：X-Y平面为电路横截面所在平面，Z为传播方向，电路在Dirac-δ函数激励下在z=z0处的电场分布为Ei(x,y,z0,t)，{φmn(x,y)}为基函数族，用φmm(x,y)可将微波电路中t=t0,z=z0处的场表示为：

　　(6)

其中amn(z0,t0)为第(m,n)次基函数的系数，即幅度，这样从参考面z=z0看入的微波电路可等效为一个基于基函数的等效时域多模电路.基函数的函数形式既可以是适用于一般电路的正交函数形式，也可以是特别适用于某类电路的特殊正交函数.一般说来，当电路几何结构比较复杂，不易根据电路特性选取特殊的正交函数作为基函数时，可以选取矩形脉冲函数(取网格结点的值作为整个网格的平均值，故脉冲宽度为一个网格的宽度).但因脉冲函数描述的只是系统的局部信息，因此要达到足够的精度，函数的展开项数较多.当正交函数可以有效表述电路的全局信息时，通常只需几项或十几项，就可以达到所需的精度.例如，对于均匀填充的矩形波导问题，如根据波导内的场的分布特性，把基函数选为{sin,cos}正交函数集，通常只需5项就可以满足要求.相比较之下，至少需要60个脉冲即60个结点方可较准确地描述波导系统横截面上的空间场分布.

基函数的正交性使得每一个基函数可以被视为一个独立的端口，因此上述基于基函数的等效时域多模电路就可以进一步被视为一个多端口网络.

2.等效多端口网络特性的计算

冲击函数的频谱是无限宽的，因此不能直接使用FDTD算法求解系统的冲击响应函数.FDTD-Diakoptics使用高斯脉冲调制波作为激励，通过加窗Fourier变换技术，求得有限带宽微波电路的冲击响应函数.其中，高斯脉冲激励的调制频率为电路工作频带的中心频率，脉冲宽度和脉冲时间采样间隔取决于频率分辨率和带宽.尽管激励脉冲具有有限带宽导致FDTD-Diakoptics求得的冲击响应函数中包含了加窗带来的影响(称此时的冲击响应函数为准冲击响应函数)，但是只要满足下述条件：使用FDTD-Diakoptics分析整个电路特性时，各个子电路使用具有相同频谱特性的激励脉冲，计入加窗对时域脉冲的展宽效应，最终得到的冲击响应函数的频域响应是足够准确的.

五、FDTD-Diakoptics应用实例及讨论

本文以一个波导带通滤波器的特性分析为例说明该算法的应用.图3为一个具有5个膜片的矩形波导带通滤波器(WR34).按照本方法首先将该滤波器分为5个部分，使用FDTD对其进行计算，求出在所有连接参考面处(图中虚线所示)的场分布.FDTD计算中，高斯脉冲调制函数为：f(t)=AmaxA(x,y)exp［-((t-t0)/T)2］.sin(2πf0t)，其中调制频率f0为WR34-TE10模单模工作频带的中心频率；A(x,y)为激励幅度空间分布，Diakoptics算法中需计算所有可能存在的基函数单一激励时的响应，所以A(x,y)依次选为每一个基函数.激励函数幅度Amax取决于其沿传播方向的衰减及计算精度，基本原则是达到不连续性处和观察面处的场仍具有足够大的幅度.T的取值要保证在激励脉冲的频谱上截止频率点处的能量具有足够小的值.本例中，WR34的单模工作频带为：fTE10=17.369GHz,fTE20=34.738GHz，f0=26.0535GHz,T=200(ps),t0=3T,Amax=10，基函数为φn(x)=sin，相应的系数an(z0,t)如图4所示(由于文章篇幅原因，只给出一个结果).图5为用本文方法得到的滤波器频率特性，图中可见该结果与FDTD结果吻合很好.

图3　五膜片WR34波导带通滤波器示意图
 
　　　　　　　　　　　　　　

图4　本文方法得到的图3中第一个子电路反射波基函数的系数

图5　图3所示WR34波导滤波器的频率特性

六、结　　论

本文介绍了一种分析复杂微波电路的新方法：FDTD-Diakoptics方法，它可克服传统的FDTD方法需要大内存、长计算时间的弊病，并可充分发挥FDTD可易于研究复杂几何结构电路的优势，经作者的若干分析设计实例证明，该方法不但比较灵活，且具有较高的精度，是一种比较有效的微波电路仿真分析方法.