复合频率信号的频谱分析在现代数据分析中起着重要作用。复合频率信号的主要特点是：由有限个单频信号线性叠加形成，背景噪声较小(通常小于-20 dB)，各分量之间存在频谱干扰[1]，一般仪器难以对其各个分量进行精密检测。复合信号幅频测试仪，在兼备频谱分析仪功能的前提下，解决了其对于复合信号各频率分量不能智能识别以及对信号幅频测量的精度普遍不高的难题。本文结合SoPC在数字信号处理领域并行性、灵活性的优势[2]，通过对包含两个单频分量的复合信号的幅频测试，给出了一套基于SoPC的复合信号幅频测试的解决方案，最终在Altera DE1开发平台上验证。
1 系统工作原理
    复合信号幅频测试系统是闭环反馈的测试系统，通过多次采样运算的方法来实现精确测量。其原理框架图如图1所示。

    对采样信号进行汉明窗加载处理，信号频谱能量泄露的问题得到有效解决[3]。但是由于FFT本身点数的限制，存在着栅栏效应，即存在最小分辨频率ΔF：

    假设输入信号是频率为f0的正弦信号s(t)，由于加入Hamming窗后，s(t)的频谱序列主瓣满足汉明窗频谱函数W(ω)[4]，W(ω)函数的极值点是真实的频率点。假设真实极值点为k，设k向下取整点为FFT所得序列的极值点设为k′，则次极值点为k点向上取整点，设为k″。由此可得，极值点k的左右两侧的频谱序列值之比为：

2 系统方案实现
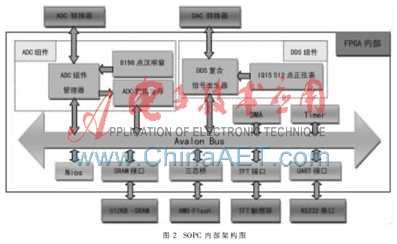
    本系统在SoPC中嵌入一个Nios II 软核，用来进行系统的整体控制和部分数字信号处理任务。Nios II软核选用全功能型CPU核，在100 MHz系统时钟下，拥有最高101 DMIPS的运算性能。SoPC内部框架图如图2所示。其中ADC采样缓存组件和DDS复合信号重建组件为自定义组件。

2.1 ADC采样缓存组件设计
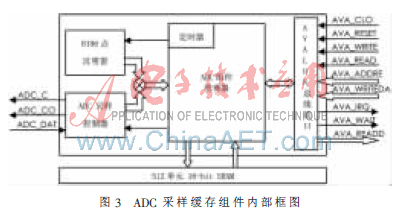
    在Nios II微处理器监控下，ADC采样缓存组件完成指定频率下ADC采样、缓存和汉明窗加载的功能，有效节约了Nios II CPU时间，提高了SoPC系统的数据处理性能。其内部框图如图3所示。每采样满256个点后，ADC采样缓存组件会向Nios II发出一次中断，这时Nios II通过DMA组件进行数据的读取。由于将512单元16 bit的SRAM分成2个256单元SRAM块，所以ADC采样数据的缓存与DMA组件数据的读取互不干扰，可以同时进行[6]。

2.2 DDS复合信号重建组件设计
    在外部DAC、有源低通滤波电路的配合下，DDS复合信号重建组件可以完成用户指定频率及幅度下的单频信号或者包含两个单频分量的复合信号的生成，生成信号的频率范围为1 Hz～100 kHz，频率分辨率小于1E-6，幅度步进1 mV。DDS复合信号重建组件生成复合频率信号，其中主信号频率为15 kHz，幅度为1 000 mV，次信号频率为100 kHz，幅度为250 mV。
2.3 系统软件设计
    复合信号幅频测试仪的软件系统由Nios II下位机部分和VB上位机部分组成。本文只对本系统IQMath运算库设计、复合信号处理算法等较为关键部分进行阐述。
2.3.1 基于Nios II 定点数软核的IQMath运算库设计
    TI公司IQMath函数库运用，使得该公司定点数DSP在浮点数运算上拥有了与浮点数DSP几乎相同的运算效率[7]。与TI公司定点数DSP一样，Nios II软核拥有强大的定点数运算能力，包括单指令桶型移位寄存器、单指令进行32×32 bit乘除法得到32位结果、计算64位和128位乘积专用指令等功能。因此，本文专门为Nios II定点数软核编写了基于Nios II软核的IQMath库，通过定点数运算来等效浮点数运算，使得在现有Nios II的软核上进行高效率、高实时性的DSP运算得以实现。目前已经完成了基于Nios II软核的IQMath库的部分常用函数设计，如表1所示。

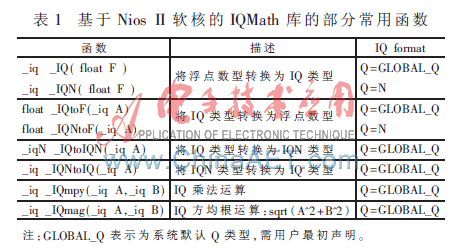
    在全功能Nios II软核(系统时钟100 MHz)的模式下，通过基于Nios II软核IQMath库的运用，8196点的FFT的运算时间由原来传统浮点型运算所需要的1.02 s变为了现在模式下的75 ms，运算速度提高了13.6倍。本方法与目前常见的在Nios II软核中嵌入自定义浮点数运算核(用户自定义指令)相比，虽然运算的速度较后者略有下降，但是有效节约了硬件资源，同时软件程序的可移植性、通用性得到提高。
2.3.2 复合信号处理算法
    复合信号处理算法完成对采样数据的分析处理，并且最终获得主、次信号的频率、幅度信息，其算法流程如图4所示。在一些特殊情况下，对算法进行了专门处理，以提高系统性能。

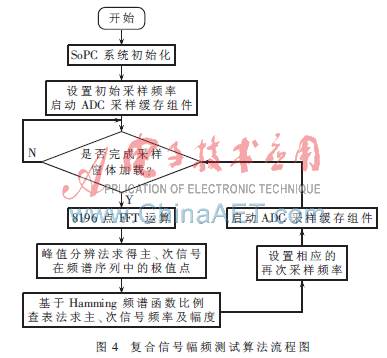
    (1)最大、最小频率点处理
    当复合信号中较高频率分量与较低频率分量的频率比值大于两个数量级时，频谱序列中较小频率分量趋向于0点并受到直流量等诸多因数的影响，进而导致对其测量精度的恶化。本系统采用了欠采样的方法处理这种情况。根据采样定理，只要采样频率fs为：

其中K为非负整数，可以保证较高频率分量位于频谱序列的高频π处，而对于低频信号就可以通过增加K的值获得足够低的最小分辨频率，进而实现对较小频率分量的精确计算。
    (2)最小频率分辨率实现
    由于主、次信号的频率分辨需要至少2.5个最小分辨频率的间隔，在首次250 kHz的定频率采样以后，系统将根据目前信号的测试数据降低再进行频率采样，一般定为大于较大频率点2.5倍的ΔF最小整数倍数，进而减少主信号对次信号的频谱干扰，提高系统测量的精度值。
3 系统指标测试
    在系统评测中，本系统测量信号反应时间为1.5 s，最大频率分辨范围为10 Hz～100 kHz；主信号测量频率平均误差为2.1E-6，主信号测量幅度平均误差为0.136%；次信号测量频率平均误差为4.7E-6，次信号测量幅度平均误差为0.674%；在满足系统要求精度的前提下，最小频率分辨率<0.08%；生成指定正弦信号平均频率误差为1.6E-7，平均幅度误差为0.34%。本系统与目前常见的AT5010频谱分析仪相比，除了具备对于复合信号分辨的功能外，在频率测量精度上也有着明显的优势。
    本文根据复合频率信号的特点设计了一种基于SoPC的复合信号幅频测试仪，实现在1.5 s内对复合频率信号中主次信号频率、幅度信息的精确计算，以及用户指定信号的生成。本文给出的基于Hamming窗频谱比例查表法，可以有效处理FFT变换中出现的栅栏效应这一技术难点；基于Nios II软核的IQMath库函数的开发实现，有效提高了Nios II定点数软核进行复杂运算的能力。本系统在Altera 公司的DE1开发板上实现。
参考文献
[1] 丁康，张晓飞.频谱校正理论的发展[J].振动工程学报，2000，13(1).
[2] 李兰英.Nios II嵌入式软核SoPC设计原理及应用[M]. 北京：北京航空航天大学出版社，2006.
[3] LYONS R G.Understanding digital signal processing[M].北京：机械工业出版社，2005.
[4] 方体莲，洪一.利用FFT校正两个密集信号的频率和相位[J].雷达科学与技术，2005(6).
[5] 张松.基于FFT的正弦信号频率估算新方法[J].大理学院学报，2009(8).
[6] Uwe Meyer-Baese.Digital signal processing with field programmable gate arrays[M].北京：清华大学出版社，2008.
[7] 苏奎峰.TMS320X281x DSP原理及C程序开发[M].北京：北京航空航天出版社，2008.