0 引言
集成运算放大器广泛应用于电子电路的设计中，可以进行信号的放大、运算(加、减、乘、除、对数、反对数、平方、开方等)、处理(调制)以及波形的产生和变换。积分器和滤波器就是运放器件辅以外围电路后的两种典型应用电路。当外围电路较为复杂时，输入／输出关系的表征就会变得较为繁琐和困难。Proteus软件具有模拟电路、数字电路和单片机应用系统的设计和仿真功能，是目前能够对微处理器进行较好仿真的软件，真正实现了从概念到产品的设计。本文探讨了使用仿真软件设计电路的可行性，并给出了典型的电压反馈取样电路设计方法。
1 积分器和滤波器工作原理
1．1 积分器工作原理
积分器的基本电路和实际应用电路如图1(a)，(b)所示。积分器的基本电路输入／输出电压关系如下：
在实际应用中，积分器的反馈电容C与电阻RF并联，其输入／输出电压关系如下：
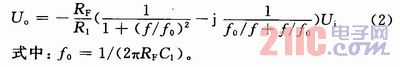
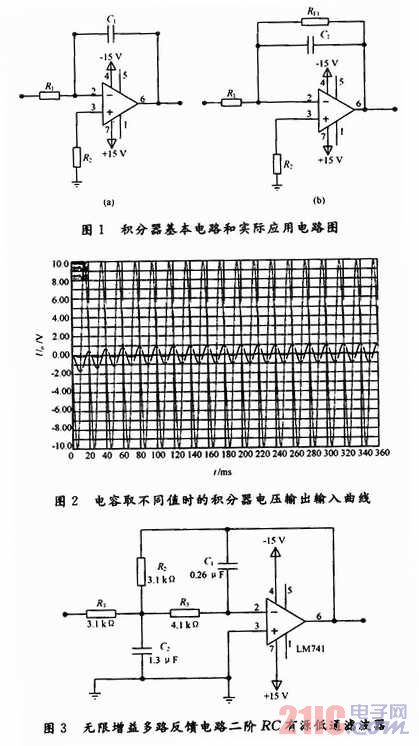
当输入的工频信号幅值为5 V时，RF和R1的固定比值分别取为20 kΩ和10 kΩ。采用Proteus仿真软件对电容取值不同的输入／输出进行了仿真验证，结果如表1和图2所示。
可见，当输入频率大于f0时，电路为积分器；当输入频率小于f0时，电路为反相器。低频电压增益为：
1．2 滤波器快速设计
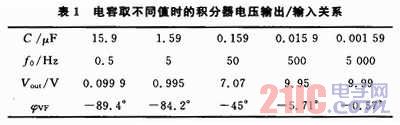
无限增益多路反馈二阶低通滤波器电路如图3所示。
设计步骤如下：
(1)根据截止频率，从表2中选定一个电容C的标称值，使其满足下式：
(2)从表3查出与AV对应的电容值及K=1时的电阻值，将电阻值乘以K后，得到电阻的设计值。滤波器的基本性能参数为Q=0．707，AV=-R2／R1。
2 电压反馈取样电路设计
2．1 滤波器移相补偿
滤波器是改善电能质量的有效措施，但相移计算起来较为繁琐，如式(5)所示：
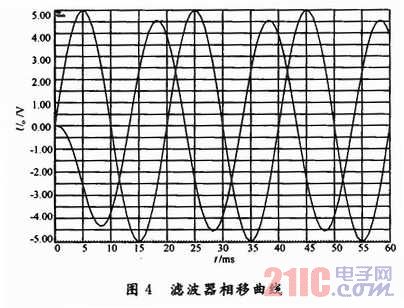
为了克服不足，通过软件仿真可快速得出相移大小，在需要同步的电路中为移相电路提供准确数据。图3的输入／输出电压曲线如图4所示。其中输入电压幅值为5 V，频率为50 Hz。
由图4可见，相移大小为
，得出θ=122°。输出电压也可由理论近似计算相等，而得到的精确值为4．56 V。
2．2 电压反馈取样电路
电压反馈取样电路由移相、全波精密整流和积分放大电路三部分组成，如图5所示。移相电路用以将输出侧的交流电压形成两路正交信号。将全波精密整流设计成输入／输出间的比例为1。积分放大电路对合成后的脉动直流信号作平滑放大处理。
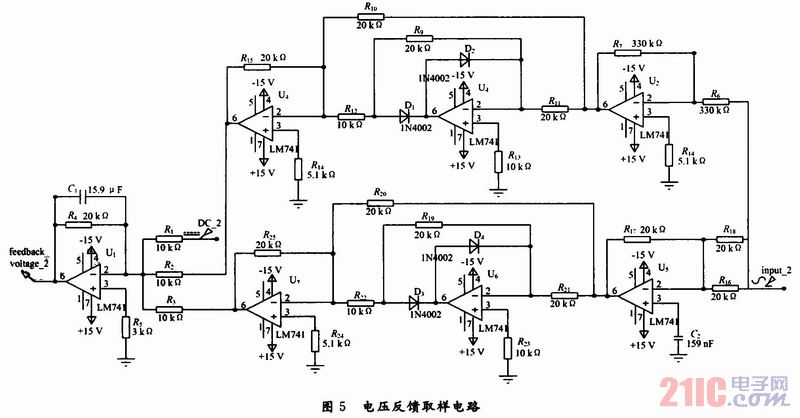
以对输入幅值2 V的工频电压信号取样为例，经过移相和全波精密整流后，作为积分放大器的输入信号，是两路为2|sinωt|和2|cosωt|的正交信号，合成为uf=2(|sinωt|+|cosωt|)作脉动变化的直流信号，因为1≤(|sinωt|+|cosωt|)≤
，考虑到RF／R1的反相放大作用，积分放大电路的输出信号uf在0～5．66 V之间变化，图6给出电容分别取15．9μF和1．59μF时的输出电压曲线。当电容为15．9μF时时间常数τ=RC=0．318 s，经过5τ=1．59 s到达稳定状态；当电容为1．59μF时的时间常数τ=RC=0．031 8 s，经过5τ=0．159 s后达到稳定状态并与图中曲线衰减规律一致。一般集成电路器件的输入电压在10 V以内，通过理论计算获得脉动直流信号的积分输出变化规律较为困难，可以通过软件仿真的方法得出输出值的变化规律，在积分放大器的输入信号中加以基准源，即可限制输出信号的幅值。对于图5可取基准源信号为-4．5 V。最终可获得正纹波很小的反应输入电压变化的直流信号。
3 结语
对滤波器和积分器的工作原理进行了说明，指出在实践设计过程中，当运算放大器外围器件较多，输入／输出关系需要精确考虑，而理论计算繁琐或较为困难时，采用软件仿真是准确、有效、便捷的辅助手段。以滤波器的相移和电压反馈取样电路为例，详细说明了采用软件仿真验证的设计过程，可以使用该法设计其他电子电路，本文设计的电压反馈取样电路极具参考价值。