认知无线电中基于非合作博弈的功率控制算法
2008-11-19
作者:冯 冀, 罗新民, 罗俊平
摘 要: 针对认知无线电" title="认知无线电">认知无线电中的功率控制" title="功率控制">功率控制问题,基于非合作博弈" title="非合作博弈">非合作博弈模型,提出了一种新的效用函数" title="效用函数">效用函数,证明了该博弈中纳什均衡的存在性和唯一性。设计了一种分布式功率控制算法并证明了其收敛性。讨论了几个参数对系统性能的影响。仿真表明,该算法可实现对认知用户发射功率" title="发射功率">发射功率的有效控制。与SINR平衡算法和Koskie-Gajic算法相比,本算法既保障了每个认知用户的QoS需求,又增加了系统吞吐量。
关键词: 功率控制; 认知无线电; 非合作博弈; 效用函数
认知无线电CR(Cognitive Radio)是一种提高无线电通信频谱利用率的新技术,为解决当前效率低下的频谱管理方式与不断增长的频谱资源需求之间的矛盾提供了一种新的解决方案[1]。发射功率是认知无线电中的重要资源,该资源如果得到有效利用,就能减小认知用户对授权用户的干扰,同时使认知用户享受更好的服务质量QoS(Quality of Service),增加系统容量。
近年来,众多学者在功率控制领域做出了许多成果[2-6],而博弈论(Game Theory)解决功率控制问题也被学者所关注[7][8]。博弈论是一种对紧缺资源分布式配置问题的求解方法。该方法算法复杂度低,所需全局信息少,适合应用于认知无线电中[1]。
参考文献[6]提出了一种基于信干噪比SINR(Signal to Interference Plus Noise Ratio)平衡的分布式功率控制算法(简称SINR平衡算法)。该算法能够保证每个认知用户的服务质量。但其收敛信干噪比固定,不能随着多址干扰和噪声的变化而变化。参考文献[7]提出了一种基于价格函数(Price Function)的功率控制算法(简称Koskie-Gajic算法)。该算法可通过适当降低SINR来大幅降低发射功率,但各用户的目标SINR无法充分保证。参考文献[8]提出了一种表征单位电池能量传输比特数的效用函数。
本论文根据无线数据网络中用户QoS满意度的特点,引入一种新的效用函数,提出了一种基于博弈论的功率控制算法。该算法能够解决认知无线电系统中分布式的功率控制问题。论文证明了该效用函数的纳什均衡存在性、唯一性及算法的收敛性,并对算法性能进行了仿真。
1 系统模型
考虑一个采用CDMA制式的中心辐射式认知无线电网络。设该网络中某小区有N个认知用户和1个基站。基站负责频谱空穴检测和频谱资源分配。在授权用户的空闲频段上,网络采用CDMA工作方式;一旦检测到该频段被授权用户占用,便及时通知认知用户切换到备用频段。假设基站已经完成了频谱资源的分配。设第i个用户的扩频带宽为W,单位Hz;传输速率为Ri,单位为b/s;发射功率为pi;认知用户i到基站的链路增益为hi;基站处的背景噪声为δ2。则第i个认知用户在基站处的信干噪比定义为[8]:
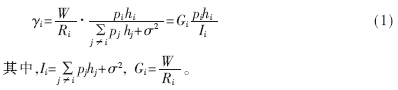
2 基于非合作博弈的功率控制
2.1 非合作博弈功率控制模型
非合作博弈功率控制模型表示为NPCG=(I,{Pi},{ui})。其中,I={1,2,…,N}表示参与功率控制的用户集合;Pi表示认知用户i的策略空间,即发射功率集合,各认知用户在一次博弈中选择的策略构成功率矢量p=(p1,p2,…,pN)。ui(p)=ui(pi, p-i)表示用户i的效用,即对所选择策略的满意程度,其中p-i表示除了认知用户i之外的N-1个认知用户的策略。认知用户选择策略的原则是最大化自己的效用,使博弈稳定于纳什均衡(Nash Equilibrium)点。
2.2 新的效用函数
在无线数据网络中,认知用户的效用随着信干噪比的增加而增加,但增加的速度会随着信干噪比的增加而减小,增大到一定的信干噪比后,效用会接近于常数。此时再增大发射功率反而会浪费电池能量。根据分析,定义一种基于信干噪比满意度的新效用函数。对认知用户i有:
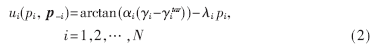
其中,γi为认知用户i基站处的信干噪比,γitar为认知用户目标信干噪比,αi为陡峭系数,λi为价格系数。
新效用函数由两部分组成。前一部分是以超过目标信干噪比的差值为自变量的反正切函数,表征认知用户对信干噪比的满意程度。当自变量趋于无穷大时,反正切函数的值收敛到一个常数,这符合认知用户对信干噪比满意度的特点。陡峭系数可以控制反正切函数的陡峭程度,实现在发射功率和信干噪比间的折衷:陡峭系数较小,曲线较平坦,当信干噪比较大时认知用户才能满意;陡峭系数较大,曲线较陡峭,信干噪比只需稍大于目标值,认知用户就能达到最大满意度。
后一部分是价格函数。对认知用户进行价格惩罚的目的是使之不再一味增大发射功率和提高信干噪比。通过价格的强迫手段达成“合作”效果,引导认知用户合理利用系统资源。因此认知用户牺牲一定的信干噪比后,发射功率可大幅降低,电池寿命得以延长,同时对其他认知用户造成的干扰降低。
2.3 纳什均衡和新算法的迭代公式求解
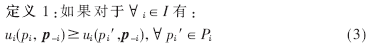
则这个策略(pi,p-i)是纳什均衡点。
纳什均衡也可以用对应反应的概念来描述。

2.4 纳什均衡解的存在性唯一性和算法收敛性
下面给出新的非合作功率控制博弈的纳什均衡存在性的证明。
定理1:新的非合作功率控制博弈存在纳什均衡。
文献[8]和文献[9]指出,如果以下条件满足,则非合作博弈存在纳什均衡:
(1) Pi是欧氏空间RN中非空的、闭的、有界的凸集;
(2) ui(p)=ui(pi,p-i)在p上连续,在pi上拟凹(quasi-concave)。
证明:每个认知用户的策略空间定义在[0,Pimax],这是一个实数的、有界的闭区间,条件1满足。显然ui(p)在p上是连续的。下面证明在pi上是拟凹的。
效用函数ui(p)对pi的二阶微分为:
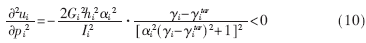
可知ui(p)在pi上是凹函数,凹函数也是拟凹的。因此满足条件2。所以新的非合作功率控制博弈存在纳什均衡。
定理2:新的非合作功率控制博弈的纳什均衡唯一。
根据定义,纳什均衡点处满足 。证明纳什均衡点唯一,只须证明对应反应
。证明纳什均衡点唯一,只须证明对应反应 是一个标准函数(standard function)[8][9]。一个函数如果满足下列三个性质就是标准的:
是一个标准函数(standard function)[8][9]。一个函数如果满足下列三个性质就是标准的:

因此当式(7)满足时,新的非合作功率控制博弈的纳什均衡点唯一,新算法收敛于唯一点。
3 仿真结果及性能分析
首先分析新算法各参数对发射功率和信干噪比的影响。考虑第1节所述的认知无线电网络中某一小区。各个认知用户等间隔地分布在距离中心基站1 000m的范围内,初始功率均为5×10-15W。当前后两次迭代的功率差小于10-5W时,迭代结束。主要仿真参数:扩频带宽5MHz,发送速率10kb/s,背景噪声5×10-15W,信道增益0.007 5×d-3.6(d为用户距离基站的距离)。
3.1 价格系数的影响
设陡峭系数为50,用户数为40,目标信干噪比为9,给出不同价格系数下,发射功率和信干噪比随认知用户与基站距离变化的关系图,如图1和图2所示。
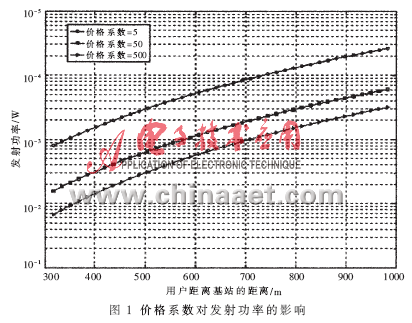
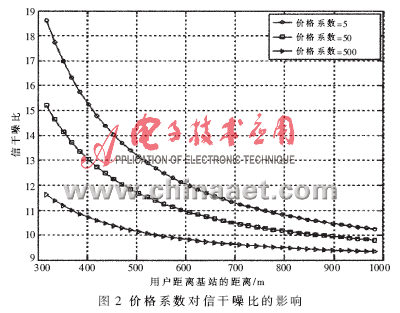
当价格系数增大,认知用户的发射功率减小时,信干噪比减小。由于认知用户的功率消耗减小,电池寿命延长,同时也减小了对其他认知用户的干扰。引入价格函数的目的是抑制各个认知用户在非合作博弈中“自私地”最大化自己效用的行为。定量分析可知,认知用户以牺牲少量信干噪比为代价,发射功率却得到了大幅降低(少于原来的1/10)。
3.2 陡峭系数的影响
设价格系数为50,认知用户数为40,目标信干噪比为9,改变陡峭系数,给出不同陡峭系数下,发射功率和信干噪比随认知用户与基站距离变化的曲线图,如图3和图4所示。
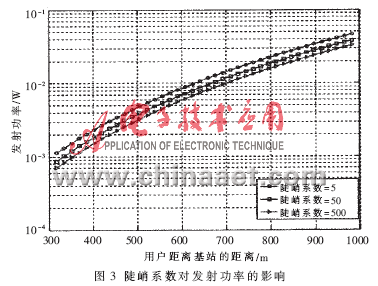
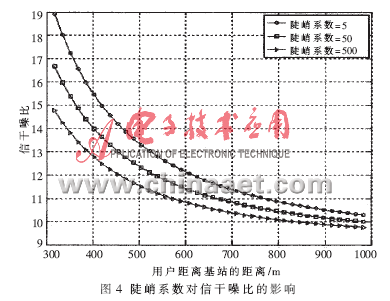
陡峭系数减小,认知用户发射功率增大,信干噪比增大。因为陡峭系数越大,效用函数曲线越陡峭。此时用户只需较小的发射功率,使得信干噪比稍稍大于目标值信干噪比,就可以使效用达到比较大的程度,认知用户对当前的QoS就满足了。反之,陡峭系数越小,认知用户对信干噪比要求较高,于是以发射功率增大来换取信干噪比的提高。陡峭系数体现了认知用户信干噪比、发射功率的折衷关系。
3.3 算法性能分析
从认知用户需求和系统性能两方面分析算法性能。为直观起见,将本算法和SINR平衡算法及Koskie-Gajic算法进行比较,包括认知用户平均发射功率、平均信干噪比和系统吞吐量。系统吞吐量采用以下香农公式表示:

3.3.1 平均发射功率与平均信干噪比
设价格系数为5 000,陡峭系数为500,目标信干噪比为9,给出平均发射功率和平均信干噪比随用户数变化的曲线图,如图5和图6所示。
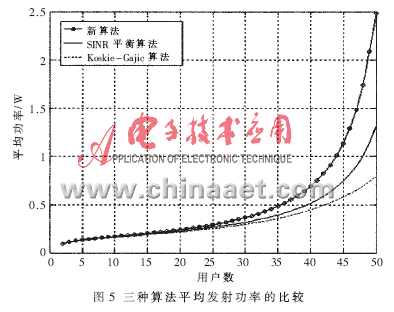
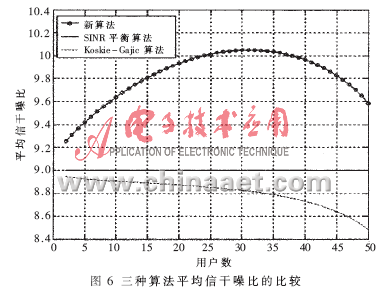
在不超过小区容量的前提下,SINR平衡算法的信干噪比一直保持在目标值上,不随用户干扰和环境噪声的变化而变化,造成资源利用率下降,系统吞吐量降低。Koskie-Gajic算法无法保障认知用户的信干噪比,因此对信干噪比要求严格的通信系统来说该算法就失去了意义。而新算法有最低信干噪比的保障,且信干噪比可以灵活调整,使系统资源利用率得到提高。3.3.2 系统总吞吐量
设认知用户数为30和40,给出平均发射功率与总吞吐量的关系如图7所示,其他参数同3.3.1节。
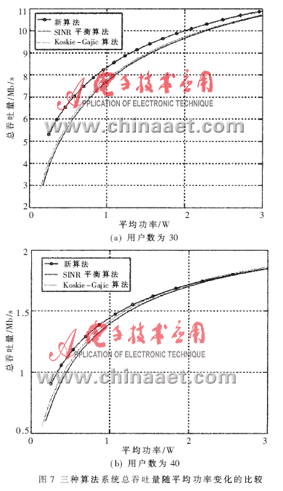
从图7可知,新算法对系统吞吐量的提高较之另外两种算法比较明显。当多址干扰加剧(认知用户数增大),随着发射功率的增加,Koskie-Gajic算法的吞吐量比新算法略有提高。但此时Koskie-Gajic算法中用户的目标信干噪比已经无法保证,在QoS要求严格的系统中这是不可接受的。此时系统吞吐量的提高已经失去意义。 对于SINR平衡算法,虽然认知用户的信干噪比要求得到了保证,但仅仅是满足要求。某些认知用户由于距离基站近或信道条件好,本可以获得更高的信干噪比,而SINR平衡算法限制了这一点,造成了系统整体性能不能充分发挥。Koskie-Gajic算法则过分强调对认知用户发射功率的控制,而忽视认知用户最基本的QoS需求。新算法既考虑到每个认知用户的QoS要求,又兼顾到系统吞吐量,通过调整参数控制发射功率,降低了认知用户间的干扰,提高了认知无线电系统性能。
本文设计了一种新的反正切型效用函数,提出了一种认知无线电系统中基于非合作博弈的分布式功率控制算法,证明了纳什均衡的存在性、唯一性和算法的收敛性。仿真表明:通过调整参数,可有效控制认知用户的发射功率,降低认知用户间的干扰;认知用户的QoS需求得到保证,且算法有较好的收敛性;与SINR平衡算法和Koskie-Gajic算法相比,该算法在相同的平均发射功率下可以获得更高的吞吐量。但本算法的收敛性受到了式(7)的制约,使得陡峭系数和价格系数不能随意变化,系统性能受到限制。这需要在以后的研究中加以改进。
参考文献
[1] HAYKIN S. Cognitive radio: brain-empowered wireless Communications[J]. IEEE Journal on Selected Areas in Communications, 2005,23(2):201-220.
[2] ZANDER J, KIM S. Radio resource management for wireless networks[M]. New York: Artech House, 2002.
[3] GRANDHI S, BIJAYAN R, GOODMAN D J. Distributed power control in cellular radio systems[J]. IEEE Transa-
ctions on Communications, 1994,42(234):226-228.
[4] ZANDER J. Performance of optimum transmitter power control in cellular radio system[J]. IEEE Transactions on Vehicle Technology, 1992, 41(1):57-62.
[5] NOVAKOVIC D M, DUKIC M L. Evolution of the power control techniques for DS-CDMA toward 3G wireless
communication systems[J]. IEEE Communications Surveys, 2000,3(4):2-5.
[6] FOSCHINI G J, MILJANIC Z. A simple distributed autonomous power control algorithm and its convergence
[J]. IEEE Transactions on Vehicular Technology,1993,42(4):641-646.
[7] KOSKIE S, GAJIC Z. A nash game algorithm for SIR-based power control in 3G wireless CDMA networks[J].
IEEE/ACM Transactions on Networking, 2005, 13(5):1017-1026.
[8] SARAYDAR C U, MANDAYAM N B, GOODMAN D J. Efficient power control via pricing in wireless data networks
[J]. IEEE Transactions on Communications, 2002, 50(2):291-303.
[9] YATES R D. A framework for uplink power control in cellular radio systems[M]. IEEE Journal on Selected Areas in Communications, 1995,13(7):1341-1347.

