陈新光 李翔宇 孙义和 清华大学微电子学研究所(北京 100084)
引言
粒子探测系统是用于获取基本粒子的能量或时间等信息的信号采集、处理系统,广泛应用于高能物理、核物理、深空探测等辐射检测中,是粒子物理等基础学科研究的主要实验装置,同时普遍存在于核医学、交通安保等应用核技术的生产生活领域。粒子探测器读出电路" title="读出电路">读出电路是核电子学中很重要的一类电路系统,它读取来自核探测器的电荷信号,通过处理得到入射粒子的能量、时间和位置信息 [1]。
由于数字电路的发展,在上世纪九十年代,人们基于数字信号处理技术提出了新的脉冲能谱分析技术和系统,基于数字信号处理的读出电路最大的好处在于其能更灵活地综合成各种最佳滤波器,从而达到最高的信躁比,得到更好的能量分辨率[2],而这些滤波器有些是很难或者是不可能通过模拟电路实现的。
梯形滤波成形算法" title="梯形滤波成形算法">梯形滤波成形算法,是将输入的阶跃信号或者指数衰减信号成形为梯形脉冲输出,当只考虑电压噪声和电流噪声时,且探测器电荷的收集时间不为零时,已经证明,梯形滤波器是最优滤波器[3],并且适合用数字方法实现 [4]。本文给出了一种数字梯形滤波器的优化的结构设计方法。
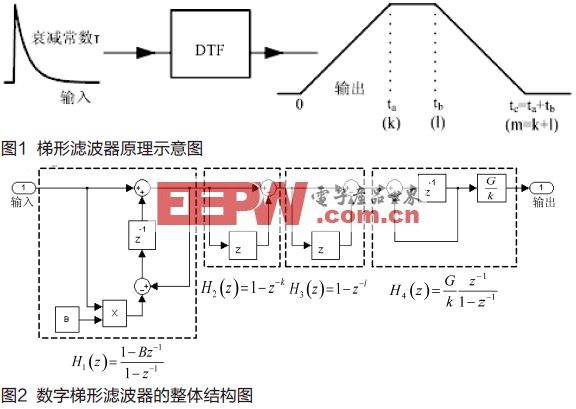
数字梯形滤波器的整体结构
针对读出电路前置放大器输出为指数衰减的情形,数字梯形滤波器的原理如图1所示,它是将指数衰减的输入信号转换为梯形脉冲,其传递函数如下式所示。
()()()()()11211111klzBzzzGHzkz−−−−−−−−=− (1)
其中,Fτ为输入指数信号的衰减时间常数;()sFexpBtτ=−为离散化参数,G为梯形滤波器的增益;梯形的上升沿宽度为k,上升沿与平顶宽度之和为l,因此平顶宽度为l-k。ts为对系统的采样周期。实际使用中, 由前放反馈回路RF-CF的值或实验预先确定,斜边长度k由噪声特性确定,所以必须根据不同的噪声环境调整斜边长度k,而平顶宽度则取决于探测器的电荷收集时间tC(前放输出上升时间)[5]。
很明显,可以将滤波器分解成四个子模块,其传递函数可以表示为:
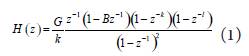
其中:
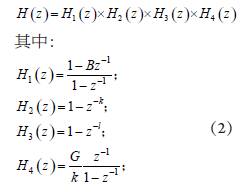
这样分解的目的是降低了系统设计的复杂度,对整个滤波器采用一种结构形式来实现是不可能的,而且需要的运算资源太多,很难找到最优的结构,所以一般采用简单的子模块并联或者是级联的方法来实现复杂的滤波器的结构。多个子模块级联存在一个级联顺序的问题,一般来说,要求出最佳配对和级联次序是很难的,但是可以通过遵循一些简单的规则就几乎可以得到好的结果,这些规则主要是为了避免具有高的峰值增益的子系统,因为它们可能会引起溢出,并且可能把量化噪声扩大[6]。在我们这个具体应用中,()1Hz的输出是会产生溢出,但是经过分析这个溢出对运算结果没有影响,所以可以把()1Hz安排在第一级,而为了避免剩下的积分单元产生溢出,把积分单元()4Hz安排在最后一级,其他两个的模块的结构一样,先后次序没什么影响,这样,确定了梯形滤波器各个子模块的次序。
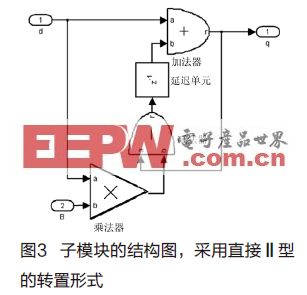
对四个子模块单独设计,再级联就可以得到整个滤波器的整体结构,最终的滤波器整体结构如图2所示,下面详细介绍各个模块的设计。
H1(z)的结构设计
结构设计指的是将线性常系数差分方程描述的系统用加法、乘以系数和延迟等基本运算模块的互联所组成的结构来表示。不同的结构,不仅需要的资源是不一样的,更重要的是,在数值精度有限的时候,它们在性能上可能有很大的差异,这个也是为什么要结构设计的原因。
滤波器的结构有很多形式,例如对于IIR滤波器,就有直接Ⅰ型、直接Ⅱ型以及他们的转置形式,而这些形式又可以通过级联和并联组成更加复杂的结构。这些结构之间的差别在于:
1. 直接Ⅰ型和直接Ⅱ型所需要的延迟单元数目为传递函数中分子和分母延迟单元数目之和,而它们的转置形式所需要的延迟单元数目为分子分母中延迟单元数目的最大者,所以直接Ⅰ型的转置形式和直接Ⅱ型的转置形式所需要的延迟单元较少。
2. 直接Ⅰ型的转置形式和直接Ⅱ型的极点实现在前面,直接Ⅰ型和直接Ⅱ型的转置形式的则相反,零点实现在前面。实现一个极点相当于积分操作,输出有可能产生溢出,而零点相当于微分操作,输出可能产生较大的截断误差。这样,他们的先后次序对系统性能影响很大,需要根据输入信号的形式选择零极点的实现次序。
对于()1Hz子模块,它有一个极点和一个零点,输入信号是指数衰减信号,如果先实现极点,那么就相当于对输入的指数衰减信号积分,必然会产生溢出,得到错误的结果,所以只能采用先实现零点的方式,也就是选择直接Ⅰ型或者是直接Ⅱ型的转置形式,考虑到减小延迟单元的个数,选择直接Ⅱ型的转置形式作为()1Hz子模块的实现结构,得到其结构图如图3所示。
延迟数可调的延迟模块设计
在子模块H2(z),H3(z)中,都含有延迟数很大的延迟单元kz−,lz−,为了适应不同的噪声环境,还需要延迟数目k,l是可调的,其实现结构如图4所示:
如图4所示,延迟模块的核心是一个双口RAM,但是数据不是在寄存器中流动,而是通过改变写和读的地址来实现延迟的,它的实现原理可以总结为以下几点:
● 通过输入地址计数器控制依次写入数据;
● 通过输出地址计数器控制依次读出数据;
● 延迟单元个数由异步复位时对输入地址计数器和输出地址计数器赋初值的差异来确定。
● 由于输出不能有不确定的值,所以在每一次复位之后,如果输出地址计数器所指向的存储单元的值不确定,就输出0,否则输出地址计数器所指向的存储单元的值。这个需要一个复位计数器来控制是输出0还是M中的值。
这样,只需要在复位之前设定 DelayNum的值,就可以在复位的时候对输入地址计数器和输出地址计数器赋值来设定延迟单元的延迟数为DelauNum。而且,这样的实现方式对于降低功耗也是是很有作用的,例如,对于一个延迟数是100的延迟单元,如果采用一般的实现方式,数据在寄存器中流动,那么每个时钟触发沿有100个寄存器需要读写,而采用上面所用的方式,只需要对两个寄存器指向的RAM单元读写就可以了,虽然增加了一些外围控制电路,但是开销相对很少。此外,由于可以采用工艺厂商提供的双口RAM宏单元,相对于寄存器组实现方式,可以大幅度降低芯片的面积和功耗。


H4(z)的实现结构
对于模块H4(z),它包括了一个比例因子,积分器单元和一个延迟单元,它的结构很简单,可以采用如()1Hz同样的结构,即直接Ⅱ型的转置形式,这样可以把积分器和延迟单元放入同一个结构,可以减少一个延迟单元;另外可以调整滤波器增益G的值使得比例因子Gk的值为2-n,这样,可以通过数据转换的方法来实现除法,例如,如果积分器的输出是20位,而通过数据转换只取其高14位作为滤波器的输出,那么就相当于除以64了,这样就不需要除法器或者是乘法器这样的运算单元来实现了,而且这只是改变了滤波器的增益,对滤波器的性能没有影响。
实验结果
本文所介绍的数字梯形滤波器设计经过FPGA验证,实现了正确的功能。图5是实际测量得到的输入输出波形图,图中上方波形是前级模拟放大器的输出波形,它经过ADC量化后
图5 示波器采集的实验系统的输入输出波形输入数字滤波器,下方的波形即是经过本文设计处理后输出梯形滤波结果再由DAC恢复出的模拟波形。
结语
本文实现了数字谱仪系统中常用的梯形滤波算法的结构设计,通过采用最佳滤波器结构以减小所需要的运算单元和延迟单元,并保证其在有限精度运算时性能不受到影响。通过采用延迟数可调的延迟单元模块,可以改变梯形滤波器上升时间和平顶时间的宽度,以适应不同的噪声环境,最后通过FPGA验证了数字梯形滤波器结构设计" title="滤波器结构设计">滤波器结构设计的正确性。

