0 引言
小电流接地系统中发生单相接地时,由于故障点的电流很小,而且三相之间的线电压仍然保持对称,在一般情况下,都允许再继续运行1~2小时,而不必立即跳闸,但为了防止故障进一步扩大成两点或多点接地故障,应及时发出信号,及时消除故障。但在现场运行中,单一故障选线方法的准确度较低,原因在于:小电流接地系统零序阻抗大,并受故障接地过渡阻抗的影响,故障电流小,故障线路与非故障线路的区别不明显;受各种干扰因素的影响,故障选线装置测量到的故障特征量(如零序电流、零序功率方向等)具有很大的模糊性和不确定性。
神经网络是模拟人类生理上的神经机制的计算模型,其中一种典型网络,也是最为成熟的一种网络为多层前馈神经网络又称BP(Back propagation)神经网络。BP网络在电力系统的各个领域有了广泛的应用,但在小电流接地选线中还没有较为成熟的应用,这是由小电流接地选线的故障特点及 BP网络容易陷入局部极小点以及学习能力有限所共同决定的。针对此问题,本文提出将遗传优化神经网络用于故障选线中,通过对故障时的各种特征量的综合判别,来大幅度提高故障选线的准确率。
1 算法原理及网络模型
遗传算法[2]是一种新型的,根植于自然遗传学和计算机科学的优化方法。其本质是将优胜劣汰、适者生存的原理及遗传机理抽象出来,形成了一种非常使于计算机实现的算法。遗传算法的计算过程是将实际的优化问题编码为染色体,实际问题的目标函数则用染色体的适应函数表示、在随机产生一群染色体的基础上,根据各染色体的适应函数进行繁殖、交叉、变异等遗传操作,产生下一代染色体。适应函数值的大小决定了该染色体被繁殖的机率,从而反映了适者生存的原理。
遗传算法能够收敛到全局最优解,而且遗传算法的鲁棒性强,将遗传算法与BP网络结合起来,不仅能发挥神经网络的泛化的映射能力,而且,使神经网络具有很快的收敛性以及较强的学习能力。遗传算法与神经网络结合主要有两种方式:一是用于网络训练,即学习网络的连接权值;二是学习网络的拓扑结构。本文主要将遗传算法用于神经网络的训练。
BP神经网络模型如图1所示:BP网络分输入层、隐含层和输出层,层与层之间采用全互连方式,在同一层单元之间不存在连接关系。信号在网络中是单方向向前传播的。
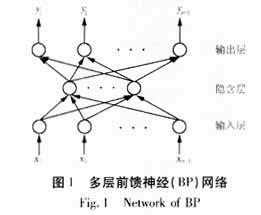
BP网络的每一层连接权值都可以通过学习来调整,未经遗传优化的BP网络的权值调整请见参考文献[1]。
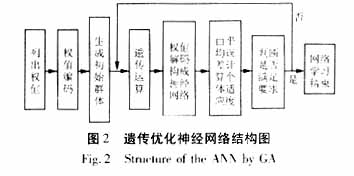
在遗传优化的神经网络中,层与层之间的连接权值用1、0表示,相连为1,不相连为0。在神经网络训练时,首先列出神经网络所有可能存在的神经元,将这些神经元所有可能存在的连接权值编码成二进制码串表示的个体,随机地生成这些码串的群体,进行常规的遗传算法优化计算。将码串解码构成神经网络,计算所有训练样本通过此神经网络产生的平均误差可以确定每个个体的适应度。具体过程见图2。这样,可以很好地解决神经网络容易陷入局部最小的问题,并且可以大大提高神经网络的学习能力。
2 输入、输出量的选取
在中性点不接地电网中,假定有K条馈电线路,则在神经网络输入、输出量选取如下:
2.1 输入量的选取
根据馈电线路数K,每条馈线输入数据共有N个,则共有K*N个输入节点,每条馈线输入数据分别为:
1) 零序测量导纳Yoi[3]
根据电网正常运行时的零序回路,利用消弧线圈适当的脱谐状况和位移电压的相应改变,可将每条馈线零序阻抗的不对称分量,即对地导纳计算出来。如果所有的零序导纳都不超过正常运行时电网限定的允许值,则无故障;当任何一条馈线发生单相接地故障时,就相当于产生了一个附加的不对称电源,这就会导致零序电压和馈线零序电流的总和量发生变化,此时同样计算出该条馈线的对地导纳。将计算出的馈线对地导纳输入神经网络,作为第一组输入数据。
2) 零序电流幅值
单相接地短路时,流过故障元件的零序电流在数值上等于所有非故障元件对地电容电流之和,即故障线路上的零序电流最大,所以零序电流幅值的大小,也是判别故障线路的有效数据。故将各条馈线的零序电流作为第二组输入数据。
3) 五次谐波分量
从过渡电阻的非线性可知故障点本身就是一个谐波源(金属性接地是经电阻接地发展而来的),且以基波和奇次谐波为主,根据谐波在整个系统内的分布和保护的要求,使用五次谐波分量为宜。NES(中性点经消弧线圈接地系统)中的消弧线圈是按照基波整定的,即有![]() ,可忽略消弧线圈对五次谐波产生的补偿效果,因零序电流五次谐波分量产生在NES中有着与NUS(中性点不接地系统)中零序电流基波分量相同的特点,根据上述零序电流幅值法原理,将其经消弧线圈所得五次谐波分量取其电流幅值,作为第三组输入数据。
,可忽略消弧线圈对五次谐波产生的补偿效果,因零序电流五次谐波分量产生在NES中有着与NUS(中性点不接地系统)中零序电流基波分量相同的特点,根据上述零序电流幅值法原理,将其经消弧线圈所得五次谐波分量取其电流幅值,作为第三组输入数据。
4)序分量测量值Is
根据参考文献[4],利用对电流正、负序分量的有效值进行相加,得出一综合测量值Is将其作为第四组输入数据。
在此神经网络中,仅选择了4组输入数据,在实际应用中,可以根据实际情况,加入其它数据,以更好地进行选线。
2.2 输出量的选取
在此网络中,共选取K+1个输出节点,代表1至K条馈线,第K+1个节点代表母线,传统的输出1代表有故障,0代表不故障的绝对关系灵活化,其值可以取[0,1]区间的任一数值,再将其输出数值进行判断,大于0.5判为故障,小于0.5判为不故障。
3 网络学习及训练
选取一有10条馈电线路的输电系统,如图3所示:
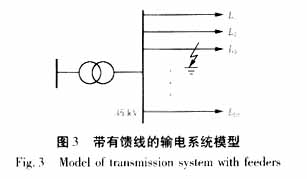
此输电系统中,L1~L4为电缆线路,L5~L10为架空线路。
对此网络进行学习训练。根据训练的实际情况,选取64个隐含节点,则依据上述原理,生成一个有4×10×64×2位的个体,然后依据遗传优化神经网络的算法原理,进行网络训练。在此实际网络中,例如,当L3馈线发生接地短路时,则神经网络的理想输出为[0 0 1 0 0 0 0 0 0 0],神经网络的实际输出为yi(i=1,2,...,10),为求取其适应度函数值,先求取方差![]() ,则其适应度函数取为f=100/S。可见,其适应度函数越高,方差越小,与标准选线结果也就越接近。
,则其适应度函数取为f=100/S。可见,其适应度函数越高,方差越小,与标准选线结果也就越接近。
经过87次的训练,该网络训练完成。进行实际运算得到的结果表明,其判断准确率可达90%以上。
4 结论
与传统的选线方法(五次谐波分量法、零序导纳法)相比,此方法根据多个判据的综合判定,加上采用了遗传算法进行神经网络的优化,避免了神经网络容易陷入局部最小的问题,大大提高了接地选线的准确性。但随着馈电线路的增加及隐含层接点数目的增加,会大大加大算法的计算量,考虑到单相接地故障允许运行1~2小时,随着计算机速度的不断加快,此问题已不是很重要,故在现场运行中是可行的。

