1引言
有源电力滤波器一般设计成电压源型PWM逆变器,通过控制各桥臂的全控型开关器件（如IGBT），使滤波器的输出很好地跟踪检测的谐波电流，对电网实现滤波。其主电路结构如图1所示，有源滤波器的工作实际通过LC充、放电实现，故LC参数的选择对滤波器的性能有重要影响。对LC参数的确定，往往通过经验，无疑使结果存在盲目性。也有文献采用了计算机辅助计算方法，但需模拟滤波器的工作过程，因此较复杂。本文采用了合理的假设，建立了参数确定的解析方法，该方法简单，并具有实用性。
2有源滤波器的数学模型
在有源滤波器中，每个半桥臂由全控的开关器件和与之反并联的二极管构成，很显然正向导通是可控的，反向导通是不可控的，可以用一理想开关代替每个半桥臂的开关管及二极管，得到如图2所示的等效电路，由图2可建立有源滤波器的数学模型。
有源滤波器工作时，保证每个时刻均由三个管子导通，由此得到8种工作模式：S1S2S3、S2S3S4、S3S4S5、S4S5S6、S5S6S1、S6S1S2、S1S3S5、S4S6S2。最后两种工作模式，滤波器的三相输出电流均为0，通过对谐波源分析发现，三相谐波不存在同时过零的时刻，故只分析前6种工作模式，有源滤波器实际由六组开关器件的通断组合所决定。
由图2建立描述滤波器工作情况的微分方程如下：
式中，KaUc、KbUc、KcUc为各桥臂的中点与电源中点间的电压，Ka、Kb、Kc是与主电路开关模式有关的开关系数，各开关模式下它们取值为：1/3或－1/3或2/3或－2/3。
对式（1）求解，可得到不同工作模式下的滤波器输出电流。
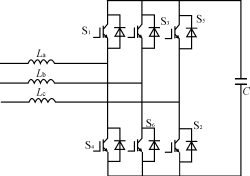
图1有源滤波器的主电路
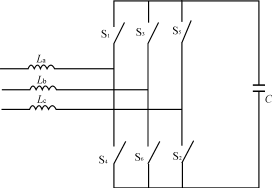
图2有源滤波器的等效电路
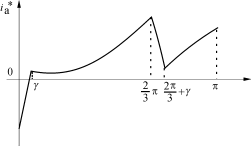
图3A相补偿电流
3有源滤波器参数确定
有源滤波器的补偿对象大部分是驱动阻感负载的可控整流设备，当整流器的触发角、负载电流、换相重叠角发生变化时，将会对参数确定产生影响。这里以三相全控桥为补偿对象，分析有源滤波器的LC参数确定的解析方法。
3.1进线电感的确定
补偿对象为一晶闸管相控整流器（三相全桥），触发角α，换相重叠角γ，直流测电流Id（假定直流侧电感无穷大，忽略电流的脉动），A相的网侧电流，如式（2）：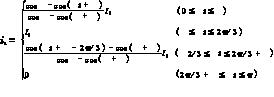
(2)
式（2）成立的条件是以触发角α为时间零点，故电网电压可表示为：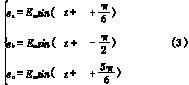
对交流侧电流波形进行付里叶分解，得到基波电流的有效值为：
(4)
同时基波电流对电压的相位差为1，则：
其中：
a=cos2α－cos2(α＋γ)
b=sin2α－sin2(α＋γ)＋2γ
因此，A相基波有功电流可表示为：
(5)
由式（2）、（5）可得有滤波器A相需补偿的电流，即控制给定电流为：
ia＊=ia－ip(6)
图3给出了ia＊的波形。
由图3可见，在半周期中（补偿电流属于半周期对称），补偿电流变化很不均匀，在换相重叠期间其变化率较大，在晶闸管导通期间，变化率又较小。
对于进线电感的选择必须满足滤波器对补偿电流的跟踪能力，所以L不宜选择过大，但L选择较小时，会使滤波器的输出电流相对于补偿电流有很大的超调，特别是在晶闸管导通期间dia＊/dt很小，因此滤波器输出电流就有很大的毛刺。综上所述，L的选择应按照换相期间的电流跟踪能力及晶闸管导通期间的电流超调两方面折衷。
为了满足电流跟踪能力，滤波器的输出电流变化率应大于换相期间对应的ia＊的最大变化率，即：
(7)
在0～γ,
在2π/3～2π/3＋γ，
令：
得：(8)
由式（1）：
(9)
为了简化计算，不直接由式（9）确定dia/dt，而由它获得dia/dt的平均值。如果有源滤波器的工作时间足够长，式（9）中的Emsin(ωt＋α＋π/6)平均作用将为零，同时，|Ka|取2/3的概率为1/3，取1/3的概率为2/3，|Ka|的平均值为4/9，则：
(10)
由式（7）、（8）、（10），得：
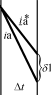
图4超调量图示
图5补偿电流
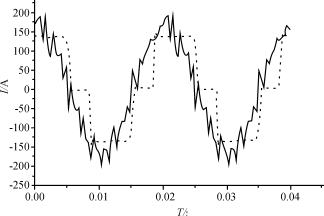
图6补偿前后的网侧电流
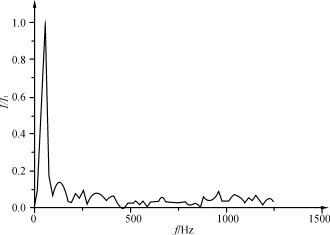
图7补偿后的网侧电流频谱
L的选择必须保证补偿电流超调量不宜过大。换相期间的超调对应了最小值，设为δ1，由图4得：
在晶闸管导通段：
结合图3，可知|dia/dt|为余弦曲线的2/3段，最小值可能为零，或|dia/dt|t=γ，或|dia/dt|t=π。当|dia/dt|取得最小值时，出现最大超调。取极端情况，|dia/dt|=0，则最大超调。为限制最大超调，取最大容许超调电流为I，有源滤波器的开关频率为f，可得：
既满足电流跟踪能力，又满足超调量限制的L取值为：
(11)
32电容量的确定
有源滤波器的工作，就是电容的充、放电过程，为了保证滤波器的性能，必须维持其直流侧的电压基本不变。电容量的选择影响了直流侧电压的波动，电容越大，电压波动越小，但带来了投资的增加。因此电容量的选择是滤波器设计的重要一环。
电容器的电压波动情况与其极板上贮存的电荷波动情况是一致的，可以通过电荷波动情况，确定电容量。而电荷波动情况又可通过电容的充、放电电流来表示。电容在一周内充电得到的或放电释放的电荷量应是电容器所必须容纳的最少电荷量。
设电容的充、放电过程变化的最大电荷量为Q1，要求电压波动小于（Δu/u)％，则极板上贮存的电荷Q为：
Q=Q1u/Δu(12)
电容量为：C=Q/u(13)
最大电荷变化量Q1可由充、放电电流对时间的积分获得。流过电容的电流由滤波器的输出电流决定，由ia＋ib＋ic=0可知在任何时刻，均有一相电流与其他两相电流反向，而这一相电流恰好是电容器的充、放电电流。
为了简化计算，作如下假设：
（1）忽略换相过程，认为直流侧电流无脉动。
（2）滤波器的输出，完全跟踪了给定电流，以给定电流作为滤波器的输出。
根据假设，得到三相给定的补偿电流，如图5所示。
电容器的充、放电电流icap为：
在各阶段充、放电的电荷Q1（最大）为：
(14)
对电网电流进行付里叶分解，得基波有功电流的有效值：
(15)
式中μ=π/3，为波形系数，由式（15）及式（5）及式（6），得：
1(16)
由式（12）～式(16)可确定电容量。
需指出，当α较小时，补偿电流波形与图5有所差别，此时补偿电流在半周期中的过零点数增加，电容的充、放电频率增加，对应的最大电荷亦与式（14）不同，将有所减小，但设计时仍可以引用式（14），只不过此时的直流侧电压波动幅度减小。同时，滤波器的输出电流是围绕给定的补偿电流进行锯齿振荡，其积分效果与对给定的补偿电流的积分效果非常接近，所以这点假设是成立的。
4仿真结果
对一台给六脉波晶闸管相控变流器补偿的有源
滤波器进行仿真（EMTP）。图6中虚线为补偿前的变流器网侧电流（Id=140A，α=30°，γ=6.4°)。设Δu/u=5％，Uc=250V，最大超调控制在10％，有源滤波器的开关频率为5kHz，根据本文方法计算，取L=0.26mH，C=66.0μF。图6中实线为电网经补偿后的电流。图7给出了补偿后网侧的电流频谱，可见，高次谐波被大大削弱，同时，功率因数得到了改善，有源滤波器获得了较好的补偿效果，从而验证了本文的方法。
5结论
本文以六脉冲晶闸管相控变流器为补偿对象，研究了有源滤波器的进线电感及直流侧电容参数确定的解析方法。通过对补偿电流的跟踪性能及滤波器的输出电流的超调的折衷，确定电感量；通过满足一定的电压变化率，而要求的直流侧电容的最小贮存电荷量确定电容，为了获得解析表达式，文中采用了一些合理的简化手段。仿真结果验证了方法的正确性。