实时系统是指能够在确定时间内执行计算或者处理事务并且对外部的异步事件做出及时响应的计算机系统[1]。实时系统最大的特点是时间的确定性，即实时性。由于实时调度算法是实时系统的核心算法，是影响实时系统实时性的最大因素，因此，对实时调度算法的研究具有重要的意义。
    RM速率单调（Rate Monotonic）算法是一种静态分配优先级的算法，它根据任务的周期来分配优先级，周期越小，任务的优先级越高[5]。而最早截止期限优先EDF(Earliest Deadline First)算法是一种动态分配优先级的算法，它根据任务的紧迫程度来分配优先级[4]。在现有实时系统中，RM算法和EDF算法是使用最多的两种实时调度算法。但是，这两种算法都是在系统中单独使用，适用面较窄，稳定性差。如果将两者结合将是一条有效的解决途径。本文在这方面进行了探索，提出了一种崭新的混合调度算法，并验证了算法的有效性。
1 相关工作
    对一些符号、概念、术语进行如下定义：
  
    任务的释放时间是指所有用来开始执行任务的资源都可用的时间，即任务开始执行的时间。任务的绝对时间限是指任务必须完成的时间。任务的相对时间限是指绝对时间限减去释放时间。
    RM、EDF调度算法基于如下假设条件[3]：
    (1)高优先级的任务可以抢先低优先级的任务。
    (2)没有任务有非抢先的部分，并且抢先的成本可以忽略。
    (3)只有处理器资源是竞争的，内存、I/O和其他资源是足够的，即无需竞争。
    (4)所有的任务都是无关的，不存在先后次序的约束。
    (5)任务集合中的所有任务都是周期性的。
    (6)任务的相对时间限等于它的周期。
    这些假设是RM和EDF算法的基础，是对理想情况的研究，在实际实时系统项目中会考虑各种实际因素的影响。文中提出的混合调度算法也是基于以上假设。
2 RM与EDF调度算法介绍及分析
    在RM调度算法中，任务的优先级与它的周期反向相关，如果任务Ti比任务Tj的周期小，则Ti比Tj的优先级高。处理器总是优先执行当前处于就绪状态的周期最小即优先级最大的任务。任务的优先级固定。
    RM调度算法对于给定周期性任务集可调度性的充分条件是[2]：
  
    另外，RM属于静态调度算法，适合于问题要求比较明确的系统，额外开销小，可预测性好。但是，由于静态调度算法一旦做出调度决定后，在整个运行期间就无法再进行更改，因此，它的灵活性不如动态调度算法，不适合于不可预测环境下的调度。EDF是一种动态调度算法，需要在变化的环境中做出反应，这类算法应用比较灵活，适合于任务不断生成的动态实时系统中。但是，动态调度算法的可预测性差并且运行开销较大。
3 混合调度算法
    关于混合调度算法的研究，参考文献[5]中提出了一种方案。对于一个任务集而言,其中任务1，2，…，k，这k个任务是具有最短周期的任务,采用固定分配优先级的RMS调度算法调度执行,而余下的任务k+1，…，m采用EDF调度算法调度执行[5]。这种调度算法只是简单地将任务分为两组，每组分别采用不同的调度算法，并没有很好地将RM与EDF调度算法结合。因此，本文提出了一种崭新的混合调度算法。

3.1 算法描述
    周期性任务集符合RM、EDF算法假设条件(1)～(5)，Ti、Tj为任务集中处于就绪态任务的绝对时间限最小的两个任务，绝对时间限分别为Di、Dj，且Di≥Dj。调度方法分两种情况：
 (1)当Di＞Dj时，若Di－Dj＜δ，则说明任务间的紧迫性高，采用EDF调度方法；若Di－Dj≥δ，则说明任务间的紧迫性低，采用RM调度方法。
 (2)当Di＝Dj时，采用RM调度方法。

 算法主要流程如图1所示。

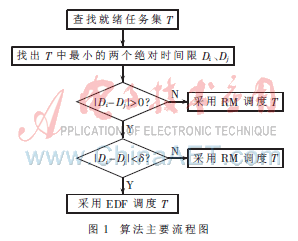
    图1中δ为阈值，其意义代表任务间的紧迫性，要根据具体实时系统进行确定。当δ足够小，如 δ=0时，混合调度算法就退化为RM调度算法；当δ足够大时，混合调度算法就退化为EDF调度算法。由此可见，混合调度算法是RM与EDF的一个很好的折中。
3.2 算法的可调度性分析
    调度算法调度任务集，调度算法的核心任务[4]是使各个任务满足各自的时间限，因此，研究调度算法的可调度性与任务的周期、执行时间等属性之间的关系、给出调度算法可调度性的判断依据是必须完成的工作。
    下面研究混合调度算法可调度性的充分必要条件。先给出一个示例，从这个特殊的示例中，可以得到一般性的结论。
    有三个周期任务，周期为p1=2，p2=5，p3=10；执行时间是e1=0.5，e2=3.5，e3=0.5；阈值选取为δ=1.5。由于是周期任务，所以任务的绝对时间限Di即为任务各个周期的结束时刻，任务的释放时刻ri为任务各个周期的开始时刻，则任务在混合调度算法下的执行流程如图2所示。

    观察上面每一个任务的第一次迭代。启动任务T1，这是最高优先级的任务，它不会被系统中的其他任务耽搁。当T1被释放时，处理器会中断正在运行的工作，而去执行T1。因此，为保证T1能够被可行地调度而满足的唯一条件为e1≤p1，这显然是一个必要条件，也是一个充分条件。
    现在考察T2。如果它的第一次迭代能在[0，p2]上找到足够的时间，它就可以成功运行。假设T2在t时刻结束，在[0，t]上释放的任务T1的总迭代次数是[t/p1]，为了使T2在t时刻结束，在[0，t]释放的任务T1的每一次迭代都必须被完成，此外还必须有可用的时间e2去执行T2，即必须满足条件：
  
其中Wi(t)是被T1，T2，…，Ti所执行的工作总量。因此可调度性的充分必要条件为：给定一个由n个周期性任务构成的集合，任务Ti能够使用混合调度算法切实可行地调度的充分必要条件是存在某个t∈[0，pi],且t为p1，p2，…，或pi的倍数，使得Li(t)≤1。

4 实验结果及分析
    对于实时系统调度算法来说，截止期错失率DMR(Deadlines Missed Rate)是衡量调度算法性能的一个重要指标。所谓的截止期错失率就是指系统中未被调度成功的任务的个数与参与调度的任务个数之比。它与调度成功率成反比，截止期错失率越高，则调度成功率越低。在实验中，比较了RM、EDF和混合调度算法在不同工作负载情况下的截止期错失率。
    实验的硬件平台是一个基于32位ARM微控制器的嵌入式系统。实时任务集由5个周期性任务组成，这个任务集的属性描述如表1所示。

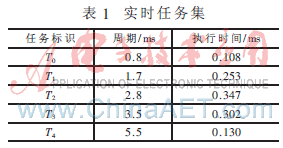
    为了对实时任务进行定期的统计，系统在实时任务建立之前，首先产生内核任务和空闲任务。内核任务具有最高优先级，每隔一段时间，对各个任务的截止期错失率进行一次统计；空闲任务具有最低优先级，当所有任务均处于不可调度状态时，可以运行空闲任务。统计结果如图3所示。

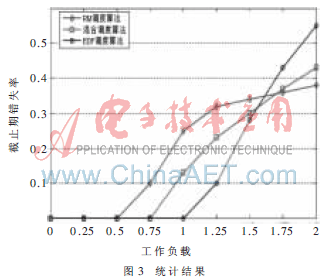
    从图3可以看出，在一定的负载范围内，RM算法和EDF算法都能够保证任务的截止期成功率，可以很好地用来调度实时任务。随着负载的增加，RM算法的截止期错失率开始增加，性能开始下降，而EDF仍然具有很好的性能，即EDF算法比RM算法可以承受更多的负载。但是当系统过载时，EDF算法截止期错失率急剧上升，性能下降很快，而RM算法则相对稳定，到一定程度时EDF算法性能低于RM算法性能。混合调度算法性能曲线介于RM算法与EDF算法之间，在一定的负载范围内，同样能够实时调度任务，而且可以承受的负载范围比RM范围大；当负载增加时，这种算法性能比EDF算法性能下降慢，表现出很好的稳定性。
    本文基于RM与EDF调度算法，提出了一种基于阈值δ的混合调度算法。这种算法可以根据需要调节阈值δ，制定符合需要的算法性能。当δ取较小值时，混合调度算法侧重于RM算法性能；当δ取较大值时，混合调度算法侧重于EDF算法性能。实验表明，在实际应用中，使用混合调度算法比单独使用RM或EDF调度算法具有更好的灵活性，能够根据需要产生理想的调度性能。

参考文献
[1] KRISHNA C M，SHIN G K.Real-time systems[M].Columbus，OH：McGraw-Hill Company，Ine.1997.
[2] LIU C L，LAYLAND J W.Scheduling algorithms for multiprogramming in a hard real time environment[J].Journal of  the ACM，1973，20(1).
[3] BUTTAZZO G.Rate monotonic vs.EDF：judgment day[J].  Real-Time Systems，2005，29(3)：5-26.
[4] 叶明，罗克露，陈慧.单调比率(RM)调度算法及应用[J]. 计算机应用，2005，25(4).
[5] 王辉.改进了的RM与EDF以及两者的混合调度算法[D].吉林：吉林大学，2004.