摘 要: 基于传统的PCA方法,提出了推广的PCA人脸识别方法。推广的PCA方法先对训练图像矩阵集进行分块,再利用传统PCA对分块得到的子训练矩阵集进行分析,得到多个变换矩阵,通过这些变换矩阵将训练图片和测试图片投影到特征空间进行鉴别。与传统PCA方法相比,提高了主元的维数,有效地增加了识别的精度。在FERET人脸库上的试验结果表明,所提出的方法在识别性能上明显优于传统的PCA方法,识别率得到了提高。
关键词: 主成分分析; 特征抽取; 推广的PCA; 特征矩阵; 人脸识别
人脸识别是模式识别研究领域的重要课题,也是一个目前非常活跃的研究方向[1,2]。它一般可描述为:给定一个静止或视频图像,利用已有的人脸数据库来确认图像中的一个或多个人。近年来,关于人脸图像线性鉴别分析方法的研究激起了人们的广泛兴趣,其焦点是如何抽取有效的鉴别特征和降维。特征抽取研究肩负两方面的使命:寻找针对模式的最具鉴别性的描述,以使此类模式的特征能最大程度地区别于彼类;在适当的情况下实现模式数据描述的维数压缩,当描述模式的原始数据空间对应较大维数时,这一点会非常有意义,甚至必不可缺[3]。
在人脸图像识别中,主成分分析PCA(Principal Component Analysis)[4],又称K-L变换,被认为是最成功的线性鉴别分析方法之一,目前仍然被广泛地应用在人脸等图像识别领域。本质上PCA方法的目的是在最小均方意义下寻找最能代表原始数据的投影。SIROVICH 和KIRBY最初使用PCA有效地表示人脸[5]。由于人脸结构的相似性,他们认为可以收集一些人脸图像作为基图(特征图),任何人脸图像可以近似地表示为该人脸样本的均值与部分基图的加权和。1991年,TURK和 PENDAND提出了著名的“Eigenfaces”方法。1997年,BELHUMEAR P N、HESPANHA J P、KRIENGMAN D J在主成分分析的基础上又给出了“Fisherfaces”方法。
以上方法在处理人脸等图像识别问题时,遵循一个共同的过程,即首先将图像矩阵转化为图像向量,然后以该图像向量作为原始特征进行线性鉴别分析。由于图像矢量的维数一般较高,比如,分辨率为100×80的图像对应的图像向量的维数高达8 000,在如此高维的图像向量上进行线性鉴别分析不仅会遇到小样本问题,而且经常需要耗费大量的时间,有时还受研究条件的限制(比如机器内存小),导致不可行。针对这个问题,人们相继提出不少解决问题的方法。概括起来,这些方法可分为以下两类:从模式样本出发,在模式识别之前,通过降低模式样本特征向量的维数达到消除奇异性的目的,可以降低图像的分辨率实现降维;从算法本身入手,通过发展直接针对于小样本问题的算法来解决问题[6,7]。
本文基于主成分分析的思想,从原始数字图像出发,在模式识别之前,先对整个图像训练矩阵集进行分块,该块中的图像尽可能具有同样的性质,从而更接近于高斯分布;再用PCA方法对每个分块得到的子图像训练矩阵进行分析,得到多个变换矩阵,通过这些变换矩阵将训练图片向量和测试图片向量投影到特征空间进行鉴别。这样做主要基于如下考虑:在传统的PCA算法中,要求训练集符合高斯分布,得到的结果才是理想的,但是实际操作中训练样本由于光照、表情、姿态等因素远离高斯分布,而改进的PCA算法通过对其进行归类训练子训练集(由于影响因素较小,更接近于高斯分布)提取主元,同时该方法可以增加主元的维数,能提供更多的有效特征。在著名的FERET人脸库上的试验结果表明,本文提出的方法在识别性能上明显优于传统的PCA方法,识别率有显著提高。

1.2 特征抽取
原始图像的维数较大,不利于直接用于分类,必须对原始数据进行降维。如何找出能代表原始图像的低维数据是进行分类的关键。

2 推广的PCA方法
2.1 思想与最优投影矩阵
传统PCA的模型中存在诸多的假设条件,决定了它存在一定的限制,在有些场合可能会效果不好甚至失效。传统的PCA算法要求标准训练样本矩阵符合高斯分布,也就是说,如果考察的数据的概率分布并不满足高斯分布或是指数型的概率分布,那么PCA将会失效。在这种模型下,不能使用方差和协方差来很好地描述噪音和冗余,对教化之后的协方差矩阵并不能得到很合适的结果。

3 实验结果与分析
实验是在FERET人脸库上进行的。FERET人脸库由200个人、每人7幅图组成:第1幅图是人脸的正面照,第2~5幅图是人脸角度的变换,第6幅图表情的变换,第7幅图是亮度的变化。每幅图的分辨率是80×80。图1是FERET人脸库的某一人的7幅图像。

FERET数据库中每张图片都有一个类别标号,代表其不同因素下采集的图片,比如标号00012_930831_fa_a,其中00012表示类别ID,930831表示样本生成时间,fa表示人脸偏转角度,a表示光照强度。本文的实验就是根据不同的图像标号来划分数据集合,从而达到外在因素较少的情况下,数据尽可能地满足简单的高斯分布。
将每类的前4幅图作为训练样本,后3幅图作为测试样本,这样训练样本总数为800,测试样本为600。首先,利用传统的PCA算法,即不对标准训练样本矩阵集进行分块,计算出不同能量系数下的识别率。再利用推广的PCA算法,分别实验两种情况:(1)将各个类训练样本的前两幅图组合为训练样本矩阵1,将各个类的训练样本的第3、4幅图组合为训练样本矩阵2,这样就将传统PCA中的训练矩阵集分为两个子训练矩阵集。对这两个子训练矩阵集进行计算得到变换矩阵[P1,P2]。再将测试样本和训练样本通过[P1,P2]投影到特征空间,对不同能量系数的情况计算得到识别率。(2)将每类的4个训练样本图片分别组合为四子训练矩阵集,然后用同样的方法计算识别率。得到的实验结果如图2所示。
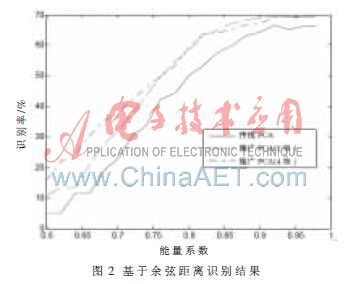
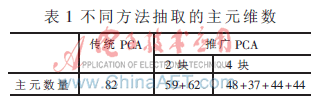
本文分别采用余弦分类器进行分辨率的计算。从图中可以看出,对推广的PCA的具体应用其识别率均优于传统的PCA方法。进一步分析其原因:推广的PCA通过对标准训练样本矩阵集进行分块,对每一个子训练矩阵集抽取主元,虽然单个子训练集抽取的主元维数可能比较低,但是由于有多个子训练矩阵集,所以总体看来其抽取的主元维数还是较传统的PCA主元维数多,因此能提高识别的精度。表1为当能量系数为0.9时不同方法抽取的主元维数。
本文提出了推广的PCA的人脸识别方法,其本质是通过对标准训练样本矩阵集做分块,并对其子块分别作PCA,抽取子块的主元。这样做是为了使影响因素较小,更接近于高斯分布,并且提高了主元的维数,在分类器进行分类时能够更好地减少误差,便于模式识别。本实验使用环境为 Microsoft Windows XP,硬件配置为Petium4,3.0 GHz CPU的计算机,优化算法采用Matlab编写。
在试验中发现,对同一数据库,对样本矩阵采用不同的分块,获得的最高识别率一般不同,如何寻求最佳分块方式有待进一步研究。
参考文献
[1] ZHAO W, CHELLAPPA R, PHILLIPS P J, et al. Face recognition: A literature survey[J]. Acm Computing Surveys, 2003,35(4):399-459.
[2] TURK M, PENTLAND A. Face recognition using eigenfaces[A]. Proc. IEEE Conference on Computer Vision and Pattern Recognition[C].USA, Howaii, Maui:IEEE,1991:586-590.
[3] 徐勇.几种线性与非线性特征抽取方法及人脸识别应用[D].南京:南京理工大学,2004.
[4] 边肇祺,张学工.模式识别(第2版)[M].北京:清华大学出版社,1999.
[5] 陈伏兵.人脸识别中鉴别特征抽取若干方法研究[D].南京:南京理工大学,2006.
[6] TURK M, PENTLAND A. Eigenfaces for recognition[J]. Journal of Cognitive Neurosciences,1991,3(1):77-86.
[7] ZHOU Ji Liu, ZHOU Ye.Research advances on the theory of face recognition[J]. Journal of Computer Aided Design and Computer Graphics, 1991,11(2):180-184.

