摘  要： 针对Lossy Counting算法，即一个基于计数的确定性方案，提出一种新的基于权重的流数据频繁项挖掘算法（Lossy Weight），扩展了流数据频繁项的作用域。Lossy Weight算法不仅可用于传统的基于计数的频繁项挖掘，还可以挖掘出在整个流数据中所占权重比重大于门槛值的数据。实验数据分析证明该方案是有效的。
关键词： 频繁项；数据挖掘；权值

    基于计数的频繁项挖掘算法适用于每个数据元组所含知识相等或近似的情况，例如用户在网页上的点击流，搜索引擎的关键词流、路由器上的IP包流等情况。但在更多的情况下，每个事务代表的知识是不相等的。如电信系统中的通话记录，每个用户的电话用时是不相同的；在证券交易中心，每笔交易的金额也是不同的。许多小客户的事务数多，但每笔事务的权值很小；重要的大客户事务数虽少，但每笔事务的权值很大。如果此时用原有的频繁项挖掘算法，将不能很好地体现那些事务数少但重要性高的客户。而采用新的基于权重的算法，则可以很好地找出那些重要性高的元素。
    本文提出的基于权重的新算法是对原有Lossy Counting[1]的扩展。不仅可以解决基于计数的频繁项挖掘问题，还能解决基于权重的频繁项挖掘问题。并且Lossy Counting算法本质上是新算法的一个特例(窗口定长，权值为1)。新算法在应用域上超出了原有算法，甚至可支持基于计数与权重的混合查询。

2 Lossy Weight算法
    本文提出的基于权重的频繁项挖掘算法(Lossy Weight Algorithm)与原有算法有着相同的定义：根据用户定义的门槛参数s∈(0，1)，输出在整个流数据中所占权重比重大于s的所有元素。
    新算法同样满足实时性的要求。在任意时间内，用户都可以提交查询，算法的结果满足以下的要求：(1)数据所有占权重比超过s的元素都被输出；(2)所有占权重比小于s-ε都不会被输出；(3)权重频繁项的误差至多为ε。
    新的算法保持了原有的Lossy Counting实现简单、处理速度快的特点。同样地，在误差的精确控制上有这样两个特点[2]：(1)存在误报可能(false positive)；(2)误报的误差可控制。

2.2 新算法的优势
    在Lossy Counting算法的基础上改进的Lossy Weight算法保留了原有算法处理效率高、占用空间少、误差精确可控的优点。同样地，算法实现简明，很容易应用到实践当中。新算法包含了原有的Lossy Counting算法，具有更大的灵活性。新算法可根据实际情况划分窗口，时间窗口大小灵活可变。Lossy Counting算法的时间窗口不可变，事实上就是窗口大小为、权值为1时的Lossy Weight算法的特例。通过灵活地选取窗大小，新的Lossy Weight算法可以得到更好的内存占用情况。
3 Lossy Weight算法的实验分析
3.1 Lossy Weight算法的特性实验
    本文采用国泰君安CSMAR(China Stock Market Ac-
counting Research)系列数据库中的中国股票交易高频数据库作为实验数据[3]。本实验采用了上海证券交易所2009年12月5日～12月7日三天的股票交易高频数据。日均20万条交易记录，总计为590 233条交易计录。在流数据频繁项挖掘实验中，将数据按时间排序，并模拟其实时到达的特性，对送达流数据处理引擎进行频繁项挖掘。
    对整个交易日所有个股的交易信息采用LW算法进行数据处理，对交易量所占比重大于l％的个股进行频繁项挖掘，然后对内存使用情况进行分析。原有的LC算法不能处理带权重的挖掘任务。在实验中，定义了不同窗口大小，并对其进行了分析。
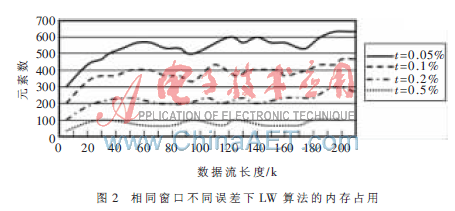
    图1所示实验是在s=l％、ε=0．1％情况下，截取交易日前5 000个数据的内存使用情况进行对比。实验显示，LW算法的窗口尺寸越小，裁剪次数越频繁，则内存使用效果越好。但过多的裁剪无疑会加大系统的负荷。所以可以根据系统的负载大小来合理地确定窗口宽度。LW算法中窗口尺寸的可伸缩性使得算法适应能力更强。

    LW算法的内存占用情况取决于窗口尺寸和错误容许度s的大小。容许的错误度越大，内存使用情况就越好。在窗口大小相等的情况下，对不同的错误容许度进行频繁项挖掘。
    图2显示了在相同窗口大小(width=1 000)情况下，不同ε的内存占用情况。实验显示，LW算法对内存空间的需求与误差ε-1近似成正比。因此，在不影响最终决策的前提下，错误容许度ε越大越好。

3.2 LW算法对LC算法的对比实验
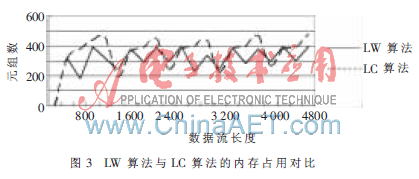
    Lossy Weight算法是对Lossy Counting算法的改进。在应用上有更广的范围，在原有的问题领域，新算法同样占有优势。LC算法的窗口大小是固定的ε-1，LW算法的窗口是动态的，可以应对任意窗口大小。这就可以面对更复杂的应用情况。在数据流量大时，扩大窗口尺寸，能起到批处理的效能。当系统较空闲时，减少窗口尺寸，以得到更好的内存使用情形。
    如图3所示，在实验中，截取交易日前5 000个数据的内存使用情况进行对比。实验设置LW窗口大小为LC大小的一半。在第一个窗口，可以看到LW算法与LC算法的内存占用是相同的。但到窗口边沿时，裁剪后的内存占用得到明显的下降。通过对整个流的处理对比，可以明显地看出LW算法具有更好的内存使用情况。

    本文提出了一种新的基于权重的流数据频繁项挖掘算法。扩展了流数据频繁项的作用域。Lossy Weight算法不仅可用于传统的基于计数的频繁项挖掘，还可以挖掘出在整个流数据中所占权重比重大于门槛值的数据。
参考文献
[1] MANKU Q S，MOTWANI R．Approximate frequency counts over data streams[C]．Proc．of the 28th Intl．Conf．on VeD，Large Data Bases．Hongkong：MorganKaufmann，2002：346-357.
[2] 潘云鹤，王金龙，徐从富．数据流频繁模式挖掘研究进展[J]．自动化学报，2006，32(4)：594-602.
[3] 朱世武，严玉星．金融数据库[M]．北京：清华大学出版社，2007：12-14.