摘  要： 将附加阻尼控制SVC应用于兆瓦级双馈型风电场并网系统，在此基础上研究了系统的暂态过程。首先建立了双馈风电机组的动态模型，水轮发电机组以及附加阻尼控制SVC的数学模型，然后仿真研究了双馈型风电场并网以后对区域系统暂态过程的影响，对比分析了风电场接入和故障情况下采用普通SVC和附加阻尼控制SVC的作用和效果，仿真结果验证了建立模型和采取方法的正确性和有效性。
关键词： 双馈感应电机；风电场；动态模型；附加阻尼控制；暂态稳定性

    风电场装机容量的增加使其对接入系统的影响越来越大，更多的并网标准要求风电场具有电压控制、无功调节、有功频率控制等火电机组具有的控制功能[1-2]。基于双馈电机的变速恒频风电机组在风力发电系统中得到了广泛应用，其主要优点是可以在变速恒频运行的同时实现最大的风能捕获，减小变流器容量，实现有功、无功功率的灵活控制。随着风力发电系统在电网中所占比重的增大，接入电网电压等级的提高，大量风电的接入改变了系统原有的潮流分布、线路传输功率以及整个系统的惯量，因此接入后系统运行的状态会发生变化[3-5]。
    风电机组接入后对电力系统的影响以及相关的稳定性问题已有了相关的分析和研究。参考文献[6]在MATLAB/Simulink仿真环境下建立基于风电机组的单机无穷大系统，分析了故障后风电系统的稳定性问题，得出了采用的输电线路越长，基于异步电机的风电系统稳定性就会越差的结论；参考文献[7]对挪威电网风电接入后的系统阻尼的分析结果表明，风电场接入容量较小时不会对系统阻尼产生影响，当风电场接入容量较大时，基于普通异步发电机的风电机组能够增强系统阻尼，对故障后的系统稳定性有利；参考文献[8]通过建模分析，得出通过控制风电机组的桨距角可以达到抑制区域间功率振荡的目的；参考文献[9]通过将双馈电机转差信号引入转子侧变流器，建立了适用于双馈异步电机励磁附加控制的PSS模型，通过仿真分析验证了所采取的方法能够改善风电场的系统阻尼。
    本文在MATLAB/Simulink仿真环境下建立变速恒频双馈风电机组模型、水轮发电机组模型以及附加阻尼控制SVC模型，对所建系统进行时域仿真，分析了兆瓦级双馈型风电场接入后的系统功率、系统机电暂态过程以及附加阻尼控制SVC在提高系统远距离输电线路输电能力、阻尼线路功率振荡、增强系统暂态稳定性方面的效果。结果表明，兆瓦级双馈型风电场接入系统后会降低系统阻尼，导致系统出现振荡，采用附加阻尼控制SVC能够有效抑制风电接入系统后的功率振荡，增强系统的暂态稳定性。
1 双馈风电机组模型
    为了能够准确进行风电接入系统后的电力系统暂态稳定性分析，需要建立适用于电力系统机电暂态分析的风电机组动态模型，使其能够充分反映在电网大扰动下的相应动态特性。
1.1 风电机组轴系模型
    为正确反映双馈风电机组在电网大扰动下的响应特性，采用两质块的轴系模型，一个质块表示风力机惯量，另一个质块表示发电机惯量。风力机与发电机通过齿轮箱连接。两质块模型表示为[10]：


其中，ΔUt为励磁系统电压测量环节输出电压；ΔUA为励磁系统电压调节器的输出；ΔUF为励磁系统负反馈环节(励磁系统稳定器)的输出；ΔEf为励磁系统输出电压。
2.4 附加阻尼控制SVC模型
    如图1所示，附加阻尼控制一般由放大环节、复位环节、相位补偿（校正）环节、限幅环节组成，其输出作为SVC电压调节器的附加控制信号。复位环节是一个高通滤波器，作用是使阻尼控制环节在t→∞(p→0)时的输出为零，屏蔽阻尼控制环节的稳态输入；相位补偿环节用来提供必要的超前-滞后特性以补偿阻尼控制环节输入(ΔP)与SVC接入点母线电压的相位滞后。本文中采用2个一阶环节，在实际中也可以用更多的一阶环节或二阶环节，以达到理想的相位补偿效果；限幅环节主要限制阻尼控制环节产生附加控制电压的调节幅度，避免超调。本文选取umax=0.15(umin=-0.15)，即限幅环节将阻尼控制环节输出调节量的幅值范围限制为±0.15 p.u.。

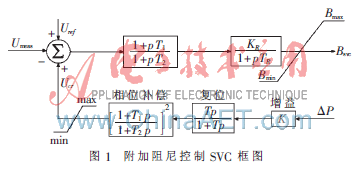
    其中，Uref为参考电压、Umeas为节点测量电压、Ucr为辅助阻尼控制输入信号、BSVC为SVC电纳参考值，这里通过加入附加控制信号改变固定的电压参考值以控制端电压的变化，Uref和Ucr相加作为控制器的有效参考值，进而使得SVC的输出电流围绕工作点波动，使接入点端电压按照期望的方式变化，达到增加系统阻尼的目的[12]。
3 风电场及系统模型
    风电场接入系统的方式如图2所示，仿真系统以某区域电网为依据进行等值处理，G1、G2为系统等值机，系统G1额定容量1 000 MVA，系统G2额定容量5 000 MVA。

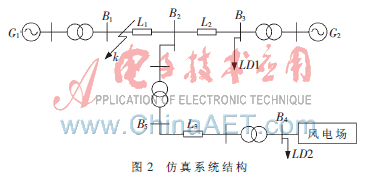
    系统G1、G2为具有原动机、励磁系统控制功能的水轮发电机组，同步发电机采用六阶模型。等值负荷LD1和LD2为恒阻抗负荷，母线B2处采用静止无功补偿器(SVC)以满足风电场接入后和故障期间系统电压的要求。风电场装机容量为150 MW，采用100台单机容量为1.5 MW的双馈风电机组进行系统等值，机组采用恒端电压控制方式。
    时域仿真分析中，将风电场接入系统后，分析对比使用普通SVC和阻尼附加控制SVC两种情况下的功率的变化和系统G1、G2发电机的转子动态过程。然后通过设置短路故障，故障位置考虑设在母线B1和B2之间输电线靠近母线B1的一端，故障在0.02 s时刻发生，经过4个工频周期后在0.1 s时刻消失，考虑系统机组在使用附加阻尼控制SVC情况下的动态过程，分析其对风电场接入后系统暂态稳定性的影响。
4 仿真分析
4.1 风电机组接入前后的时域仿真
    对比分析风电场接入系统后，使用普通SVC和附加阻尼控制SVC两种情况下，系统发电机G1有功功率、系统发电机G1、G2转子相角差、G1转子角速度的变化。
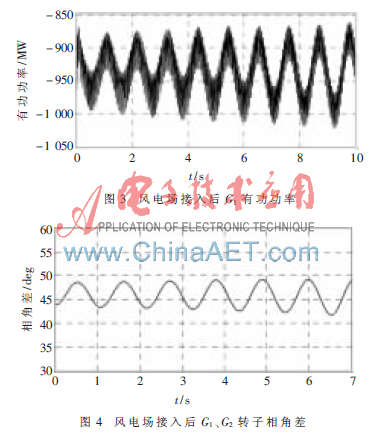
4.1.1 风电场接入后，使用普通SVC
    由图3、图4可以看出在系统配置普通SVC情况下，发电机G1有功功率出现振荡，并且振荡的幅值逐步增大，G1、G2转子相角差也出现在43°～48°之间接近于等幅的振荡，发电机G1转子角速度振荡增加，说明风电场的接入激起了系统振荡。

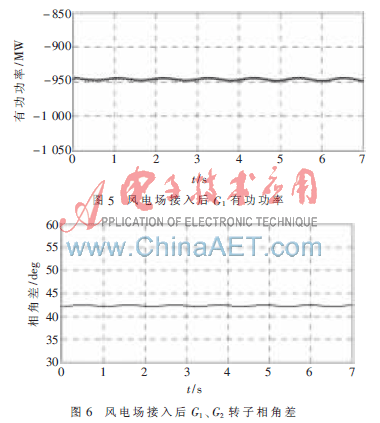
4.1.2 风电场接入后，使用附加阻尼控制SVC
    由图5、图6可知在采用附加阻尼控制SVC代替普通SVC后，G1有功功率和G1、G2转子相角差能够基本保持不变，系统振荡得到有效的阻尼和抑制作用，稳定性得到加强。

4.2 系统发生故障时的时域仿真
    以系统中发生后果最为严重的三相短路接地故障为例，分析G1有功功率和G1、G2转子相角差在采用附加阻尼控制SVC情况下的动态响应，其中设置故障时间在0.02 s时刻发生，经历4个周波后在0.1 s时刻消失。
    通过设置三相短路接地故障，分析附加阻尼控制SVC对含风电系统动态过程的影响。由图7、图8可以看出采用阻尼附加控制SVC能够在系统发生故障后很快地使转子相角差和有功功率趋于恒定，改善了系统阻尼，增强了系统的暂态稳定性。

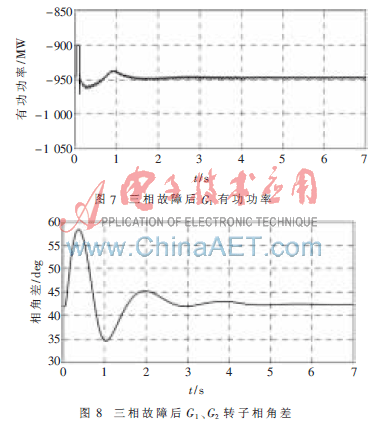
    实验结果证明，即便在恒定风速情况下(风电场本身无扰动)，基于双馈感应电机的风电场接入系统以后，会对系统的稳定性产生影响，如果采用普通SVC，经过一段时间的振荡后系统仍会失去稳定，甚至崩溃。以功率偏移作为输入量的带有阻尼附加控制功能的SVC兼有抑制系统振荡和提供系统电压支持的双重作用，能够增强风电接入后系统的稳定性。
参考文献
[1] JAUCH C,SORENSEN P,BAK-JENSEN B.International review of connection requirements for wind turbine[C]. Proceedings of Nordic Wind Power Conference,March 1-2, 2004,Gothenburg,Sweden.
[2] BOLIKS M.Grid requirements challenges for wind turbines[C].Proceedings of 4th International Workshop on Largescale Integration of Wind Power Transmission Networks for  Offshore Wind Farms,October 20-21,2003,Billund,Denmark.
[3] SHI L,XU Z,HAO J, et al.Modelling analysis of transient stability simulation with high penetration of grid-connected wind farms of DFIG type[J].Wind Energy,2007,10(4):303-320.
[4] EKANAYAKE J B,HOLDSWORTH L,WU X G,et al.  Dynamic modeling of doubly-fed induction generator wind  turbines[J].IEEE Trans on Power Systems,2003,18(2):803-809.
[5] 石立宝,戴世强,徐政.大规模双馈型风电场并网的系统暂态稳定仿真[J].电力系统及其自动化学报,2009,21
(8)：1-7.
[6] SENJYU T,SUEYOSHI N.Stability analysis of wind power generating system[C].Proceedings of The Power Conversion  Conference,Apr2-5,2002,Osaka,Japan.2002: 1441-1446.
[7] HAGSTROM E,NORHEIM I,UHLEN K. Large scale wind power integration in Norway and effect on damping in the Nordic grid[C].Proceedings of Nordic Wind Power  Conference,March1-2,2004,Gothenburg,Swed-en.
[8] JAUCH C.Stability and control of wind farms in power systems[D].Roskilde, Denmark: Ris National Laboratory, Technical University of Denmark,2006.
[9] 关宏亮,迟永宁,戴慧珠,等.并网风电场改善系统阻尼的仿真[J].电力系统自动化,2008,32(13):81-85.
[10] 迟永宁,王伟胜,刘燕华,等.大型风电场对电力系统暂态稳定性的影响[J].电力系统自动化,2006,30(15):10-14.
[11] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.
[12] 谢小荣,姜齐荣.柔性交流输电系统的原理与应用[M].北京:清华大学出版社,2006.