引言

　　时序抖动和时序噪声属于人们了解甚少的工程概念，而它们又是模拟设计和数字设计中最重要的参数。尤其是在高速通信系统中，恶劣的抖动性能会导致更高的误码率，并限制系统速度。时序抖动一般定义为数字信号在某一重要时刻相对于其理想时间位置的短时间偏离。有若干因素会影响随机时序抖动，包括宽带噪声、相位噪声、杂散信号、压摆率、带宽。相位噪声和宽带噪声都是随机的，而杂散信号是由串扰和电源耦合等各种可确定的干扰信号导致的确定性响应。如同本文稍后提到的那样，压摆率和带宽也影响抖动。图1描绘了一条非理想的正弦曲线，它包含了这三种噪声源。图2显示了一个数字信号，伴随的抖动随时间而积累。

　　本文旨在解释和论证时序抖动和这三种噪声源之间的直接关系。

　　图1. 对时序抖动产生影响的三个噪声源。

　　随机噪声与杂散信号导致的抖动。抖动会随时间积累。" border="0" height="146" src="http://files.chinaaet.com/images/20110617/8abaf8f1-2782-4990-b57c-623e91f6a1c4.jpg" width="375" />

　　图2. 时钟信号内的随机噪声与杂散信号导致的抖动。抖动会随时间积累。

　　宽带噪声对时序抖动的影响正弦波的抖动

　　所有电子元件都产生宽带噪声，尤其是放大器和逻辑器件。宽带噪声也称作噪声底，是散粒噪声和热噪声的结合。散粒噪声在二极管和晶体管中很常见，是由电荷穿越半导体结的势垒时的随机跳跃导致的。另一方面，热噪声不受电流的影响。它是由载波的随机热运动导致的，例如在MOSFET的栅极和通道阻抗范围内。热噪声功率与阻抗和温度成正比。

　　随着现代元件的工作带宽进入数千兆赫兹范围，宽带噪声对时序抖动的影响变得相当突出。例如，一个宽带放大器驱动器的带宽是40GHz，噪声系数是10dB，小信号增益是20dB，输出功率是0dBm，则它产生的噪声输出是-38dBm （-174dBm + 10dB + 20dB + 10log10（40GHz））。这导致38dB的信噪比（SNR）。在这个SNR水平，宽带噪声就是时序抖动的重要影响因素。总均方根（RMS）噪声电压是噪声底在频带内的积分。图3说明了RMS噪声是如何转化为时序抖动的。

　　图3. 噪声电压Δy穿越0V，使信号提前Δt达到阈值，从而产生了抖动。

　　从数学上来说，可以用下面的公式表示包含宽带白噪声的正弦波：

　　其中A为振幅，ω是角频率，vn（t）为时刻t处的噪声电压。随机噪声vn（t）具有高斯（正态）分布。噪声电压ƒ（vn）的概率分布（vn）为：

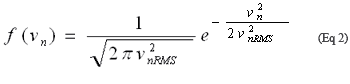
　　其中（vnRMS）为RMS噪声电压。为了理解噪声电压是如何转换为时序抖动的，可考虑把y（t）施加到抖动测量仪器（如带直方图功能的采样示波器）的输入端。每次y（t）穿越0V阈值时，直方图上就增加一个数据点。正如图3所示，在时间Δt内，存在噪声信号Δy达到阈值的可能，因此抖动被加到直方图中，时间比预期的采样点早或晚Δt。概率密度为时序抖动Δt的函数，是通过在公式2中设置vn = Δy = Asin（2πƒΔt）来计算的。结果就是抖动分布函数，如直方图所示。

　　假设Δt相比正弦曲线周期而言很小，那么可以对公式3进行简化，得到：Asin（2πƒΔt ≅ A（2πƒΔt = AωΔt。

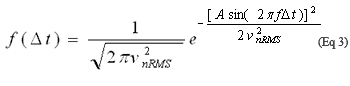
　　公式3可变为：

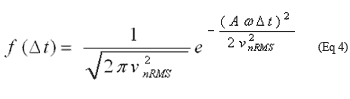
　　把公式4中各项的分子和分母同除以Aω，得到：

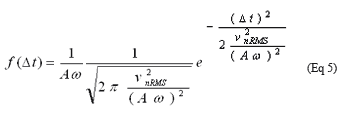
　　公式5为抖动分布函数，除比例因子1/Aω外，它与公式2中的高斯分布相似，因此，得到的RMS抖动为：

　　图4所示的测试装置用来验证公式6。纯正弦波信号和宽带噪声信号相互叠加，然后输入采样示波器，它在零交叉处测量抖动。为了确保测试结果有意义，设置的输入宽带噪声要高于示波器的噪声底。图5和图6显示了实验结果。图5表明在RMS噪声恒定时，抖动是频率的函数；图6表明频率恒定时，抖动是RMS噪声的函数。测量得到的抖动曲线和计算得到的抖动曲线之间具有相似性，证明公式6可用来把宽带噪声转化成时序抖动。

　　图4. 抖动测试装置#1：噪声和纯正弦波信号叠加。

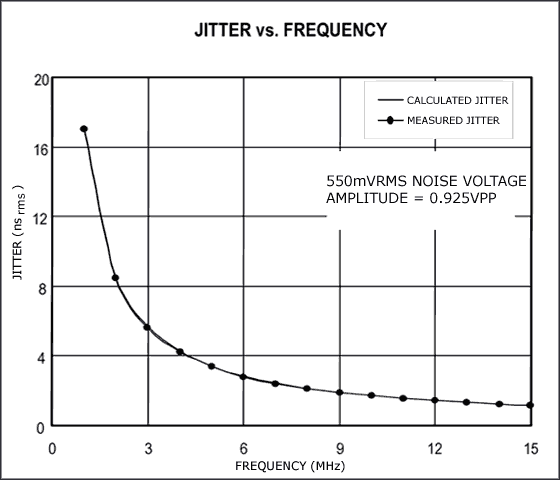
　　图5. 在RMS噪声一定的情况下，抖动为频率的函数。

　　图6. 在频率一定的情况下，抖动为RMS噪声电压的函数。

　　普通波形的抖动

　　经过稍微修改，公式6还能用于其他波形的抖动转化。根据定义，公式6中的A项是0V阈值时的压摆率S。只要已知该阈值处的压摆率，任何波形都可用于求出Δt与Δy之间的关系，这是因为vn = Δy = SΔt （图3）。把它代入公式2得到公式7：

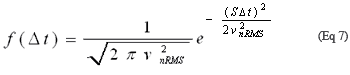
　　把公式7中各项的分子和分母同除以S，得到：

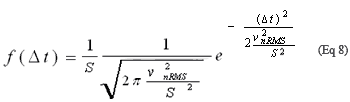
　　除比例因子1/S外，公式8与公式2中的高斯分布相似，因此，得到的RMS抖动为：

　　图4所示的测试装置再次用于验证公式9。正弦波曲线用一个压摆率可变的方波代替。在方波上升沿的50%处测量抖动。图7所示结果表明公式9是正确的。

　　图7. 在方波上升沿的50%处测量抖动。

　　图7中给出的信息引出了一个有趣的现象。似乎波形的压摆率越快，产生的抖动越小。然而，较快的压摆率要求较高的工作带宽，这增加了系统中的RMS噪声。因为RMS噪声与带宽成正比，因此系统设计者必须仔细选择压摆率和带宽，来使抖动降到最低程度。

　　相位噪声对时序抖动的影响相位噪声存在于任何有源元件和无源元件中，但它在振荡器中表现最为严重。这些振荡器包括晶体自激振荡器和时钟恢复应用中的锁相振荡器。相位噪声是一种描述频谱纯度的指标。例如，理想情况下，振荡器输出应该是一条纯正弦曲线，表示为频域中位于某个单一频率的垂线。然而，在现实情况中，振荡器存在一些噪声源，它们会导致输出频率偏离其理想位置，因此在载波（基波）频率附近，产生了一个其他频率的“裙边”效应（图8）。这些频率被称作相位噪声，是由对振荡器进行调制的噪声源引起的。它们的电平通常比噪声底高，频率接近载波频率。相位噪声通常被指定为偏离载波的某个频率处的噪声功率与载波功率之比，在1Hz带宽之内。由于相位噪声来自于噪声源对信号的频率调制，因此相位噪声不受压摆率的影响。

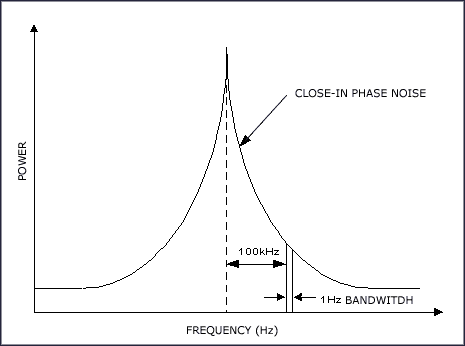
　　图8. 由于振荡器的噪声频率调制，输出频谱中出现“裙边”效应。

　　受大多数抖动测量设备能力所限，与测量低噪声信号在时域中的抖动相比，通常更容易通过测量它在频域中的相位噪声来确定其纯度。例如，多数抖动测量示波器只能测量低达1psRMS的抖动。大多数实时示波器的带宽仅为7GHz。而另一方面，相位噪声设备能获得目前最佳的低噪声示波器的噪声测量水平（在时域中远小于1ps），并提供高达40GHz的带宽。

　　在早期的文章［1-2］中我们已经探讨了相位噪声和时序抖动的转换问题。为了得到相位噪声与抖动的关系式，可以考虑把公式10作为一个带有相位噪声的正弦曲线：

　　其中A是振幅， fo是额定频率， Φ（t）为相位噪声。通常在两个或多个周期之间的0V交越处测量抖动。在0V交越处， 公式10括号内的各项为2πN：

　　其中t1为第一个零交越时刻，t2为第N个零交越时刻。两个公式相减得出：

　　两个交越点之间的时间为周期数量加上抖动：

　　TO为周期，即1/fO，Δt是N个周期后积累的抖动。把公式14代入公式13得：

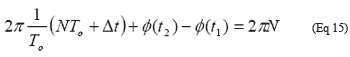
　　重新整理公式15，并消去2πN项，得到抖动：

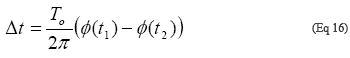
　　RMS抖动的平方为：

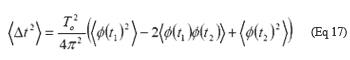
　　因为Φ（t）是个稳态过程，所以：

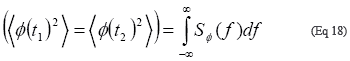
　　其中SΦ（ƒ）为Φ（t）的频谱密度，f为偏移（傅立叶）频率。公式17的中间项变为：

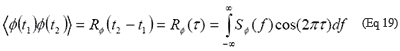
　　其中RΦ（τ）是Φ（ƒ）的自相关函数，是经过τ ≅ NTo个周期后的时间。经过N个周期后，在时刻RMS抖动的平方τ为：

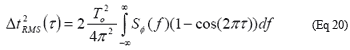
　　利用代数公式1 - cos（2Φƒτ = 2sin²（Φƒτ）），并假设相位噪声接近载波并且对称（就是从-fOFFSET到0的积分等于0到+fOFFSET的积分），公式20可以重写为：

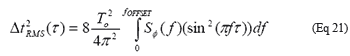
　　SΦ（ƒ）近似等于相位噪声L（ƒ） ［3］；也就是说，傅立叶频偏比载波频偏小得多： fOFFSET 《《 fO。

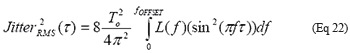
　　为了验证公式22，使用了一个相位调制电路［4］，它是图9所示测试装置的一部分。相位调制电路可以非常方便地产生无杂散、可变相位噪声信号。首先，利用采样示波器针对时序抖动测量该电路的输出，然后用频谱分析仪（没有画出）针对相位噪声测量其输出。图10显示了该电路的相位噪声图。它类似于锁相振荡器的噪声图，在这种振荡器中，相位噪声在环路带宽内是恒定的，并在带外滚降。图11给出了使用数值积分对公式22求积分后得到的相对于周期的累积抖动。图11中的曲线证实了公式22的正确性。

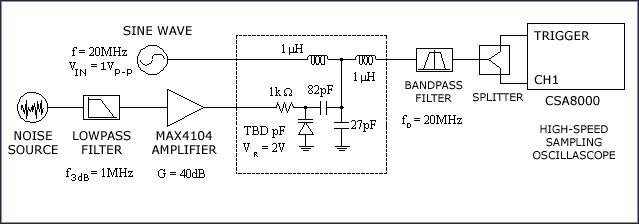
　　图9. 抖动测试装置#2：使用相位调制器产生相位噪声和抖动。

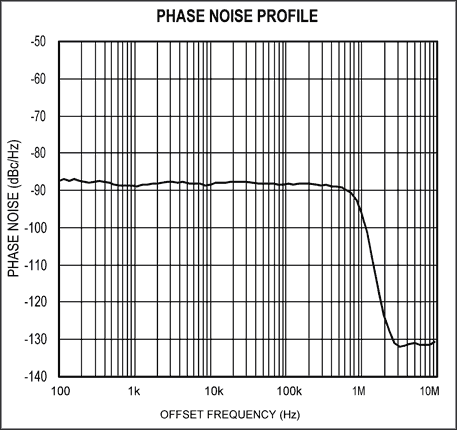
　　图10. 相位调制电路的相位噪声图形。

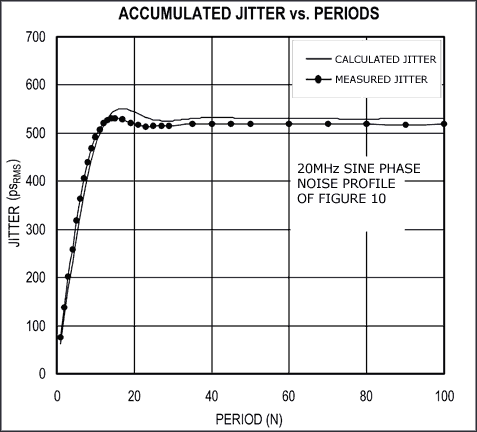
　　图11. 图形显示的是相对于周期的累积抖动，证实了公式22的正确性。

　　杂散噪声对时序抖动的影响杂散信号也对时序抖动有影响，尤其是在振荡器中。杂散信号是由锁相环基准的杂散信号、电源耦合、相邻电路的串扰、噪声源引起的。如图1所示，这些杂散信号通常表现为载波频率附近的小尖峰。公式22有助于建立杂散信号和时序抖动的关系。由于杂散只发生在特定频率，因此公式22中的积分函数可以用总和来代替：

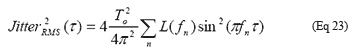
　　同样，τ ≅ NTo为经过N个周期的时间。由于公式23未假定杂散信号是对称的，所以要乘的系数为4而不是8。在计算抖动时，载波两侧的杂散信号都必须包含在内。L（fn）为杂散信号相对于载波（预期信号）的振幅，通常以dBc为单位。fn为n次谐波的频率偏移。图12是公式23的波形图，使用载波两侧的杂散信号，频偏为100kHz，振幅为-40dBc。参考文献1中验证了公式23，方法是用一条正弦波调制一个压控晶体振荡器，产生载波两侧的杂散信号（没有画出）。

　　图12. 公式23的曲线，显示了载波两侧产生的杂散信号。

　　总抖动如前所述，宽带噪声、相位噪声、杂散信号是时序抖动的三个影响因素。宽带噪声是纯粹随机和非相干的，因此它产生的抖动不累积。然而，后两者一般都产生累积抖动。总时序抖动的平方等于三种抖动的平方和。

　　结束语实验数据和计算数据之间的一致性证明了三种主要噪声源和时序抖动之间的关系。高速系统的设计人员可以利用公式9、22和23把噪声转化成时序抖动。

　　附录：计算RMS噪声电压

　　如果已知某种电子器件的一项或几项常规噪声规格，那么可以通过多种方法来确定它的总RMS噪声电压。表1列出了一些元件制造商们通常提供的噪声指标。

　　如果给定了噪声密度，就可以通过在有效带宽上对噪声密度进行积分来估算总RMS噪声，公式如下：

　　系统的典型负载阻抗ZO为50Ω，PRMS为RMS噪声功率，BW为带宽，NOISE-FLOOR是以dBm/Hz为单位的噪声底密度。例如，一个放大器的带宽为10GHz，输出噪声密度为-150dBm/Hz，则它产生的总RMS噪声电压为707µVRMS：

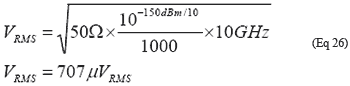
　　噪声系数（NF）常用于描述低噪声放大器和功率放大器噪声性能。可以从噪声系数推导出噪声底密度，方法是把它与50Ω电阻的热噪声相加，再加上系统增益，公式如下：

　　例如，一个噪声系数为10dB、小信号增益为20dB的放大器的噪声底密度为-144dBm/Hz。

　　已知噪声密度，就可以推出总噪声电压。

　　另一方面，运算放大器噪声特性的表现形式通常是输入参考噪声，单位为nV/。假定噪声电流可忽略，信号源阻抗远小于放大器输入阻抗，那么总RMS噪声可通过下面公式计算：

　　例如：一个输入噪声密度为8nV/、小信号增益为20dB、带宽为1GHz的放大器产生的噪声电压为800µVRMS：

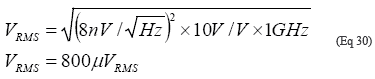
　　振荡器的相位噪声的单位通常为dBc/Hz。dBc单位表示输出噪声对期望信号功率的归一化。下面的公式可用于计算总RMS噪声电压：

　　其中PSIG为振荡器的输出功率。例如，某个振荡器在50Ω产生的功率为10dBm，输出相位噪声底为-150dBc/Hz、有效带宽为100MHz， 则输出噪声电压为224mVRMS：

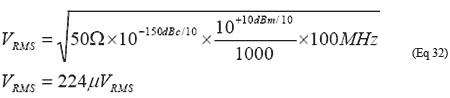
　　参考文献

　　Ali Hajimiri et. al.， “Jitter and Phase Noise in Ring Oscillators，” IEEE Journal of Solid-State Circuits， Vol. 34， No. 6， pp. 790-804.

　　Boris Drakhlis， “Calculate Oscillator Jitter By Using Phase-Noise Analysis，” Microwaves & RF， Jan. 2001 pp. 82-90 and p. 157.

　　W. F. Egan， Frequency Synthesis by Phase Lock. New York： Wilen， 1981.

　　Enrico Rubiola et. al.， “The ±45° Correlation Interferometer as a Means to Measure Phase Noise of Parametric Origin” IEEE Transactions On Instrumentation and Measurement， Vol. 52， No. 1， pp. 182-188.