摘  要： 介绍一种单片机测量时频参数时的数据处理方法,即线性地址变换法。在存储容量有效压缩的基础上,进一步分析采样数据,用软件实现可控时标,保证测量精度。 

    关键词： 测量  频率  周期  单片机  存储容量

    在智能仪表、网络通讯、过程控制等测控系统应用中,经常需要对脉冲信号的频率(或周期)进行精确测量。常用的方法是被测信号作为闸门信号,而用一个标准频率信号作为填充脉冲,在闸门周期内对标准频率信号计数,如图1所示。设计数器的值为N,则被测信号的周期T=N/f₀,频率f_x=1/T。在以单片机为核心的测控系统中,为了保证信号的测量精度,需要对大量的计数值N_i进行计算处理,这样势必占用较多的存储单元。如何压缩数据存储量,是本文要解决的主要问题。

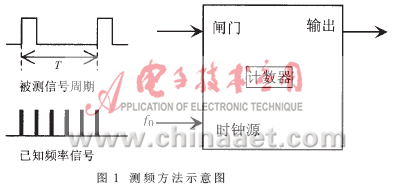
1 基于单片机系统的时频参数测量 

    当采用单片机微处理器测量信号频率(周期)时,定时器T0工作在计数方式,定时器T1工作在定时方式,T1向外部发固定频率的脉冲(时标),T0对时标进行计数。被测脉冲信号产生一个外部中断控制信号,向CPU发出一个中断请求,CPU响应中断,在中断服务程序中把T0的计数值读入数据存储器,数据转移完成后,使T0复位,重新计数， 开始新的周期测量,其测量原理如图2所示。 

2 线性地址变换 

    单片机把计数值读入存储器,是把每一个测出的周期值T_i按其时间先后顺序存入存储器中。这样,测出的每一个T_i无论是否相同都要用一个单元来存放,且随着被测信号的平均频率和测量时间t的增长,所需要的存储容量就会增加,即: 

    存储容量  M=f·t 

    如被测信号平均频率f=10kHz,则1秒约需存储容量10KB,10秒约需存储容量100KB。显然,单片机片内RAM是不能满足要求的。即使扩充外存,也不宜太大,会有一定的限制。 

    但实际上,所测出的T_i中,有相当多是相同的。如果把相同的T_i值用一个单元来存放,则可大大压缩存储容量。为此,可采用线性变换的方法,把每个T_i按(1)式转换为单元地址值,并将其内容加1,表示已有一个该T_i值。最后该单元的内容N_i就表示测量中共有N_i个相同的Ti值出现。 

    存储地址=起始地址+kT_i                     (1) 

    式中:起始地址——对应于T_i=0的存储单元地址,根据所选单片机型号任意设定。 

    k——变换比,表示出现T_i值的个数N_i用k个字节来存放。

    k=1,表示T_i对应的N_i值用1个字节存放。 

    k=2,表示T_i对应的N_i值用2个字节存放。 

    这样: 

    存储容量M=存储地址最大值-起始地址值=kT_imax (2) 

    因此,使用线性地址变换时,存储容量由测量的最大周期T_imax决定。且当采用计数方式测T_i值时,若计数时标周期为t_c,则计数器测得的T_i值实际上是T_i所包含的t_c个数。这样,存储容量可改写为: 

    存储容量M=T_imax/t_c          (设k=1)        (3) 

    若规定测量的T_imax=10ms,当设置t_c=4μs时,M=2.5KB;若要进一步压缩存储容量,可增大t_c,如当t_c=8μs时,M=1.25KB,从而可满足有限存储容量的要求。 

    单片机进行线性地址变换时,用定时器计数方法测量每一个T_i值,然后用中断服务子程序按(1)式进行地址变换,把T_i值转换为地址单元号,并使该单元内容加1。如把一次采样规定为测n个T_i值,则当把n个T_i采样完后,在存储器从起始地址开始的单元内就直接存放了如图3所示的反映被测脉冲频率波动情况的周期概率分布曲线。图3中N_i为一次采样的n个脉冲周期中出现周期为T_i的次数,N_max为N_i中的最大值,T_Nmax为对应的周期值。 

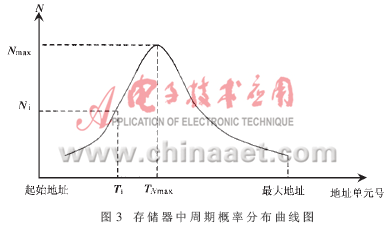
    根据测得的存储数据,由数理统计方法可计算出平均周期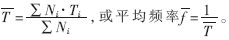 

    上述数据处理方法既保证了数据采样的信息量又节约了存储空间,较真实地反映了采样期间信号的变化情况。 

3 存储容量的压缩与测量精度的保证 

    上述数据处理方法虽然可用增大时标tc来压缩存储容量,但另一方面则可能使测试的相对误差Δ增大,其最大相对误差Δ_max出现在测量区间的低端T_{i min}时: 

    考虑测试误差,将(4)式代入(3)式,则存储容量可表示为: 

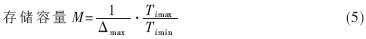
    此式表明,考虑测试误差时,要压缩存储容量就要压缩测量区间。若测量范围定为50μs～10ms,则测量区间计算值为: 

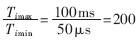
    如设定  Δ_max≤0.01,则M≥20KB。 

    因此,为了将存储容量压缩到2KB左右,又使其Δ_max≤0.01,则应压缩测量区间到20以下。 

    若把整个测量范围分成若干个区间,每个区间以不同的时标进行测试,就可满足Δ_max≤0.01,存储容量2～3KB的要求。 

    上述定标是由软件完成的。采用的方法是先用较大的时标测量一次(称为粗测),然后从概率分布曲线上找到N_max所对应的T_Nmax值,与区间定标界限系数相比较,视其所在区间确定定时器T1的时间常数,输出相应的时标脉冲。自动定标后,以新的时标重新进行测量(称为精测),精测得到的周期概率分布曲线才作为计算和控制的依据。 

    关于数据采集的软件流程如图4所示。 

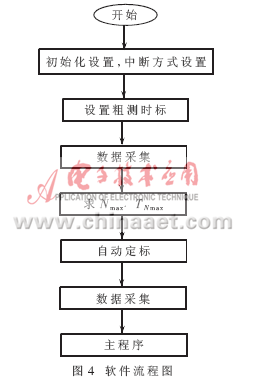
    随着单片机主频的不断提高,DSP技术的广泛应用,为时频参数的高精度测量创造了有利条件。本文提出的存储容量压缩方法,旨在提供一条解决精度与数据存储量问题的新途径,特别对于那些有一定离散度的不稳定频率信号是较为适用的。此方法已在多项数据采集测控系统中得到了应用和验证,取得了较好的效果。 

参考文献 

1 何立民. MCS-51系列单片机应用系统设计. 北京:北京航空航天大学出版社,1990 

2 沈兰荪. 高速数据采集系统的原理与应用. 北京:人民邮电出版社,1995 

3 柳义利. 高速连续频率测量. 电子测量技术,1999;25(2)