摘  要: 将生物进化的理论引入入侵检测系统,在算法中体现出基因算法的并行优势。

　　关键词: 入侵检测  生物进化理论  基因算法

　　生物进化计算理论起源于20世纪50年代末,成熟于20世纪80年代。Holland和Goldberg提出的基因算法GA(Genetic Algorithm)强调染色体的操作。本文采用GA进行实验。

　　GA通过模拟达尔文“优胜劣汰,适者生存”的原理激励更好的结构;通过模拟孟德尔遗传变异理论在迭代过程中保持已有的结构,同时寻找更好的结构,即迭代自适应随机性优化搜索算法。作为生物进化计算的主要手段之一,GA产生之初就是对自然界进化过程的一个简单模拟,并借用一些生物学术语:个体(individual):表示问题的一个可能解;种群(population):表示一组个体的集合。问题的解用定长二进制编码来表示,所以也称个体为位串(string)。在种群中,每个个体的性能用适值函数来度量,其值称为适应值或适值(fitness)。一组遗传操作(genetic operation,包括选择selection、交叉crossover、变异mutation)作用于种群上,使得种群不断进化,直到产生符合要求的个体即求得问题的最优解或次优解为止。

　　入侵检测是对以计算机系统或网络资源为目标的非法、恶意的行为或企图及那些滥用其权限的识别和反应过程的统称。目前的研究基本可以归纳为异常检测(anomaly-based)和误用检测(misuse-based)。异常检测是假设入侵活动具有不同于正常用户活动的特征,即入侵活动表现为异常。它虽然能检测到一些未知入侵,但是误警率很高,阈值很难把握。误用检测首先将已知的每种入侵方法都表示成一条入侵规则,将当前发生的活动与入侵规则集进行匹配。如果当前的活动与某条入侵规则匹配,则认为是采用该种入侵方法发起的一次攻击。商用软件多采取这种方式,其优点是对已知入侵的判断准确率高,但对未知入侵则无能为力。

　　为了增大误用检测的灵活性,可以通过概念学习的方法对入侵检测模式库中的规则进行提纯,然后利用生物进化理论中的基因算法进行搜索。

1  生物进化理论解决模式库动态提纯问题

1.1 实验在整个系统中的位置

　　本文在已有的基于改进模式匹配的IDS(Intrusion Detection System,入侵检测系统)中添加了概念学习模块。所谓改进的模式匹配是指加入了检测分步攻击的规则。例如在对主机审计日志的检测时,考虑到攻击者在入侵一个系统时往往采用一定的行为模式,而这种行为模式构成了某种具有一定行为特征的模型。因此可用这种模型所代表的攻击特征作为规则。该模块主要功能是:利用概念学习的思想,滞后进行提纯模式库。

　　鉴于进化计算运行时需消耗大量资源,为了不影响主模块(HOST)的实时检测,该模块单独运行在另一台主机上(LAB_PC)并和主模块保持通信,定期更新模式库。图1为系统相关部分的描述。

1.2 实验的描述

　　在改进的模式匹配IDS中,可以将审计事件集看作一个字符集。每个事件可看成一个字符,审计活动是一个主串,而异常行为(称作攻击脚本子集)作为一个子串,需要被定位于主串的某个位置。这样,问题被转换为:给定一个输入字符串p和一个由s所构成的模式,目标是找到p中包含一个可以被s匹配的子串。

　　在一个给定的攻击集合里,每个攻击的发生都会引发一个审计事件或事件序列。因此,可以首先计算其中所有攻击将产生的每种类型事件的数目。如果所记录到的这些事件实际发生的数目大于或等于这些事件的计算值,则可以认为相对应于这些攻击子集所作的假设是正确的。反之,认为这些攻击必定没有发生(此处借用异常检测的思想)。而满足这个条件的解可能有多个,实验的目的就是分析所记录的审计活动,在所有可能的攻击子集中寻找对系统最具威协性的攻击(最优解)。下面给出精确描述:

　　(1)式是典型的0-1规划NP-Complete。当阶次急剧增大时,使用传统的求解方法相当困难且不现实,因此采用诸如GA这类生物进化的启发式搜索办法。

1.3 基因算法的核心要素

　　GA在实现过程中,始终围绕着以下5个核心要素:参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定等。下面将围绕这几个核心要素对算法进行阐述。

　　(1)参数编码

    GA不能直接处理问题空间的参数,因此,必须把优化问题的参数形式的解转换成位串的表示形式。在编码时,结合二进制编码的优势以及出于避免海明悬崖(Hamming Cliffs)的考虑,采用Gray编码。

　　设二进制串b₁,b₂,……b_n,对应的Gray串为a₁,a₂,……a_n,从二进制编码到Gray编码的变换为:

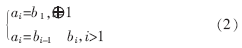
　　(2)初始群体的设定

　　群体大小L表示群体中所含个体的数量。通常,L越大GA所处理的模式就越多,生成有意义的基因块并逐渐进化为最优解的机会就越高,算法陷入局部解的危险性也就越小。但是,L增大的代价却是实验中的计算复杂度以指数级增加。反之,降低L可提高运算速度,却降低了整个群体的多样性,引发每代个体的早熟。所以一般取值为20～100。

　　(3)适值函数的设计

　　GA在优化搜索中基本上不需外部信息,仅以适值函数作为寻优依据。而且GA对适值函数惟一要求是不为负,这使得GA的应用范围极广。这里需要搜索整个问题空间,以便找出对系统危害最大的攻击子集,也就是最大化乘积W×H。实验设定根据式(3)来评估优劣,并作为以后遗传操作的依据。但是,如果仅靠适值函数来评估和引导搜索,会使求解问题所固有的约束条件不能明确表示出来。

　　式(3)中并没有考虑问题的约束条件:(EH)_i≤O_i(1≤i≤Na)。当(EH)_i>Oi时,在总计2^Ne种不同的攻击子集的假设中有一些个体是不具备现实意义的。所以必须考虑惩罚函数以减少它们的适应值,从而使约束优化问题转换成为一个附带考虑代价的非约束优化问题。同时,为避免出现早熟现象,根据Joines提出的动态惩罚函数给出适值函数如下:

　　设A为N_e×1的零矩阵,则:

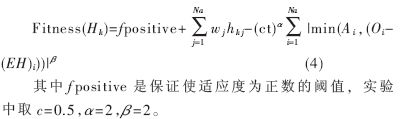
　　(4)遗传操作设计

　　本文涉及的遗传算子有:期望值选择、单点交叉、基本变异。

1.4 实验流程

　　实验通过linux下的C语言编程实现。编程环境:Red Hat7.0,GCC编译器,GDA调试器。由于GA的随机性及不确定性等特点,通常要多运行几次才能找到可靠的解。每次实验用四元组(P_c,P_m,L,a)表示。其中:P_c为交叉概率;P_m为变异概率;L为群体大小,本实验中取值为24;a为实际出现在审计活动中的攻击的数目。最后将终止代的群体中的最佳个体作为所求问题的最优解输出。实验中取P_c=0.6,P_m=0.002。

　　定义一个比率T_p来反映检测的准确程度(实际攻击所在的编码位为1的个体数比种群总个体数L)。指定T_pi为T_p在第i代的值。表1是十次平均数据结果,可以看出当进化到80代时,T_pi几乎接近1,从而得到问题最优解。

2  小  结

　　本文将生物进化的思想引入IDS,在算法中体现出GA的并行优势。实验在以下几个方面还需改进:

　　(1)如果采用动态Pm,即改进实验中采用的基本变异算子,则将变异算子与进化代数联系起来,使进化初期变异的范围相对较大,而随着进化的推进,变异的范围越来越小。这里的Pm对进化起微调的作用。例如可以采用这样的方法:首先在个体k中随机选取一个分量ki,对ki变异后的结果ki′服从N(k_i,δ₂(t))的正态分布。其中t是进化的代数,δ₂(t)随着t的增大而趋于0。当然,若δ₂(t)不同,将导致算法略微不同。

　　(2)如果某些事件或事件组对于特定的攻击普遍存在,则攻击者利用这一点向目标系统同时发起多次攻击,使实验无法找到最佳的向量表示。

　　(3)此实验模块必须和基于改进模式匹配主模块配合使用,实验模块不能独立承担实时检测义务。

参考文献

1  王正志,薄涛编.进化计算.长沙:国防科技大学出版社,2000

2  Denning D E.An intrusion detection model.IEEE Transaction on Software Engineering,1987;SE-13(2)

3  Kumar S.Classification and Detection of Computer Intrusions.PH.D thesis.Purdue University,1995

4  Goldberg D E.Genetic Algorithms in Search Optimization and Machine Learning.New York,AddisonWesley

Publishing CO,1989