摘  要： 为了有效提高混凝土抗压强度的预测精准度，利用粒子群算法优化BP神经网络初始权值和阈值，建立了混凝土抗压强多因子PSO-BP预测模型。模型以每立方混凝土中水泥、高炉矿渣粉、粉煤灰、水、减水剂、粗集料和细集料的含量以及置放天数为输入参数，混凝土抗压强度值作为输出参数，不仅可以克服BP算法收敛速度慢和易陷入局部极值的缺陷，而且模型的学习能力、泛化能力和预测精度都有了很大的提高。以UCI数据库中的Concrete Compressive Strength数据集为例进行仿真测试，结果表明：PSO-BP模型预测精度较BP、GA-BP模型分别提高了8.26%和2.05%，验证了PSO-BP模型在混凝土抗压强度预测中的有效性。
关键词： BP神经网络；粒子群算法；混凝土抗压强度；预测

    混凝土抗压强度是否符合预期规定是其质量控制的重要研究内容之一，准确预测混凝土抗压强度对施工质量的提高、工程进度的加快有着重要作用[1]。对于普通混凝土的强度，一般可以用灰水比为主要因素的线性函数来进行描述和预测。对于高掺量的粉煤灰和矿渣混凝土来说，由于其组分的增加，水化反应的机理还不完全明确，影响因素更为复杂并具有交互作用，表现为特定的非线性规律[2]。人工神经网络(ANN)是解决非线性问题的有效手段之一，其中BP网络由于结构简单、易于实现、鲁棒性强等特点，成为神经网络中运用较多的网络之一。但是BP神经网络也具有一些固有的弱点，如算法容易陷入局部极小点、收敛速度慢等，限制了它的进一步应用。
    粒子群优化算法(PSO)避免了梯度下降法中要求函数可微、对函数求导的过程，采用基于种群全局搜索策略，而且其采用的速度—搜索模型操作简单。它特有的记忆使其可以动态跟踪当前的搜索情况，调整其搜索策略，可大大缩短神经网络的训练时间[3]。基于此，本文采用粒子群算法优化BP神经网络的权值和阈值，并利用训练样本建立了混凝土抗压强度PSO-BP预测模型。然后利用此模型对测试样本进行预测，得到测试样本抗压强度值和误差，并将结果与BP、GA-BP网络进行比较，来验证该模型在混凝土抗压强度预测中的可靠性和适用性。
1 PSO-BP模型的建立
1.1 BP神经网络基本原理
    BP(Back Propagation)神经网络是一种神经网络学习算法，全称为基于误差反向传播算法的人工神经网络，由信息的正向传播和误差的反向传播两个过程组成。输入层各神经元负责接收来自外界的输入信息， 并传递给中间层各神经元；中间层是内部信息处理层，负责信息交换。根据信息变化能力的需求，中间层可以设计为单隐层或多隐层结构； 最后一个隐层传递到输出层各神经元的信息，经进一步处理后， 完成一次学习的正向传播，由输出层向外界输出信息处理结果。当实际输出与期望输出不符时，进入误差的反向传播阶段。隐含层中神经元的转换函数有多种，通常采用log-sigmoid型函数。层与层之间采用全互联的方式，以三层网络为例，其BP网络的拓扑结构如图1所示[4]。一个具有3层的BP神经网络能够以任意精度逼近任意连续函数，具有很强的非线性映射能力以及自学习、自组织和自适应能力，因此本文选用三层BP神经网络。

  

   
2.3 实验结果与分析
    对于1 030组实验数据，本文随机选取1 020组作为训练数据，用剩余10组作为测试数据。利用Matlab神经网络工具箱和PSO工具箱编制PSO-BP混凝土抗压强度预测程序，将PSO中粒子的位置映射为BP神经网络的初始权值和阈值，通过BP算法训练网络，直到网络达到性能指标。图2给出了PSO优化过程中最优个体适应度变化曲线，可见适应度值从最初的6.5经过20代左右快速收敛到了4.5。

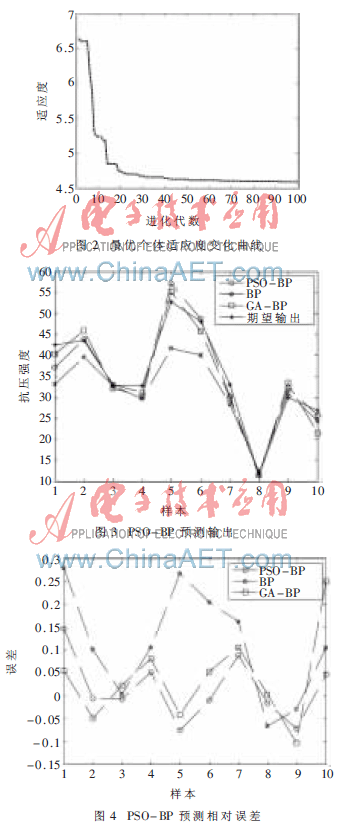
    用训练好的PSO-BP模型对测试样本进行测试，得到测试样本的预测结果。图3给出了10个测试样本的预测输出，从图中可以看出，PSO-BP模型的吻合度要比BP、GA-BP高许多。图4给出了预测相对误差，可以更进一步看出，除了个别样本，PSO-BP模型预测误差曲线在零附近的震荡和偏差都要小于BP、GA-BP模型。表1列出了PSO-BP、BP和GA-BP模型分别对10组测试样本的预测输出和相对误差。

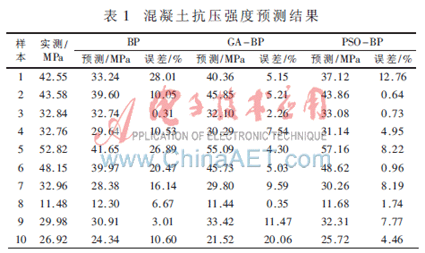
    观察表1，对于10组测试样本，预测相对误差小于15%的，PSO-BP、BP和GA-BP分别为10例、6例和9例，相对误差平均值分别为5.04%、13.30%和7.09%；PSO-BP模型预测精度较BP、GA-BP模型分别提高了8.26%和2.05%。可见，PSO-BP模型的预测准确度要优于BP、GA-BP，这为混凝土的抗压强度提供了一个更精准的预测方法。
    传统的混凝土抗压强度线性预测方法存在诸多不足，采用人工智能技术较好地解决了这个问题。将粒子群算法与BP神经网络相结合，建立的PSO-BP模型兼有人工神经网络的广泛映射能力和粒子群算法的全局收敛以及启发式学习等优点，明显提高了网络的泛化能力和运算效率。将PSO-BP模型运用于混凝土抗压强度预测研究中，结果表明该模型具有较高的预测精度，可以在混凝土工程中进行实际运用。
参考文献
[1] 季韬，林挺伟，林旭健.基于人工神经网络的混凝土抗压强度预测方法[J].建筑材料学报,2005，8(6)：676-681.
[2] 廖小辉，黄新，施俊玲，等.基于BP网络的再生混凝土抗压强度的预测模型[J].南京林业大学学报(自然科学版)，2010，34(5)：105-108.
[3] 任洪娥，霍满冬.基于PSO优化的SVM预测应用研究[J].计算机应用研究，2009，26(3)：867-869.
[4] 张鹏，赵铁军，李秋义，等.双掺粉煤灰和矿渣混凝土强度的BP网络预测模型[J].混凝土，2009(6)：16-18.
[5] 娄伟平，陈海燕，邱新法，等.基于粒子群优化神经网络的台风灾情定量评估[J].自然灾害学报, 2010，19(4)：136-139.
[6] YI D，GE X R.An improved PSO based ANN with simulated annealing technique[J].Neurocomputing，2005，63(11)：527-533.
[7] MATLAB中文论坛编著.MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010.
[8] YEH I C.Modeling of strength of high performance concrete using artificial neural networks[J],Cement and Concrete Research，1998，12(28)：1797-1808.