在许多实际工程应用中，只要求天线阵列有窄的扫描波束，而不要求有相应的增益。如高频地面雷达天线、抗环境干扰的卫星接收天线和射电天文中的干涉阵列等。采用稀疏阵列（即从规则的栅格中抽去天线单元或接匹配负载）的方法可以构造出一个降低了增益的高方向性天线阵列，以较少天线单元数达到扫描波束变窄的技术指标，从而大大降低生产成本[1]。阵列的周期性变稀会使阵列方向图出现非常高的旁瓣，稀疏阵列优化设计的主要目的就是实现旁瓣性能最优化，即尽可能地降低峰值旁瓣电平（PSL）。

    近年来，随着计算机技术的飞速发展，高效的稀疏阵列优化方法已成为研究热点。用于稀疏阵列优化的算法主要有遗传算法、模拟退火算法、分区动态规划法、粒子群算法以及最近出现的蚁群算法等。这些算法从本质上来说都是基于随机性的自然算法，在阵列大小（即可放置阵元的栅格数）超过200的稀疏阵列的优化设计当中一般并不适用 [2]，而关于大型直线稀疏阵列（阵列大小大于500）的优化问题，国内外鲜有研究。
    本文介绍的基于迭代FFT算法的大型直线稀疏阵列的优化方法是一种全新高效的优化方法，只需要很少的计算时间就能得到显著的优化效果。

2 迭代FFT算法
    运用迭代FFT算法来实现大型直线稀疏阵列优化的详细步骤为[4]：
    (1) 参数初始化，给定迭代循环总次数Num，阵列大小M，稀疏率f，旁瓣约束条件等参数。
    (2) 随机产生一个初始阵元激励数组Am。数组大小为M，有阵元的位置设置为1，无阵元的位置设置为0。阵元数目T=f×M。
    (3) 对Am作K（K>M）点的逆FFT变换，得到阵列因子AF。
    (4) 找出AF中的旁瓣区域，将旁瓣区域中不满足给定的旁瓣约束的采样值进行处理，变成旁瓣约束允许的最大旁瓣电平值。
    (5) 对处理后的AF作K点的FFT变换，得到新的阵元激励Am。
    (6) 对Am作截断处理，只保留前M个数值。
    (7) 对阵元激励Am进行归一化，其中T个幅度较大的采样值置为1，其余置为0，来完成阵列的稀疏。1表示该位置有阵元，0表示该位置无阵元。
    (8) 将归一化的阵元激励Am与迭代前的阵元激励进行比较。如果不相同，则执行步骤9；如果相同，则本次迭代循环结束。
    (9) 重复步骤(3)~步骤(8)，直到PSL达到给定的旁瓣约束条件，或迭代次数达到给定的一次循环迭代允许的最大迭代次数。
    (10) 步骤(2)~步骤(9)为一次迭代循环步骤。根据给定的迭代循环总次数，进行Num次迭代循环，就完成了整个优化流程。
    实验表明，一次迭代循环往往经过8~10次迭代便会结束，每一次迭代循环得到的最优PSL(局部最优PSL)未必能达到给定的旁瓣约束条件，但是制定合理的旁瓣约束条件，就能使局部最优PSL接近给定的旁瓣约束。因此只要进行足够多次迭代循环，每次迭代循环都以一个随机的初始阵元激励数组开始，各个迭代循环相互独立，就有很大的概率得到一个最优或近似最优的阵元分布，取局部最优PSL中的最小值作为最后的优化结果。因为运用FFT快速算法计算方向图函数，并且每次迭代循环的迭代次数很少，所以整个优化过程很快就能完成。
3 计算机仿真结果
　  接下来分别给出了阵列大小为1 000的大型直线稀疏阵列在不同稀疏率、不同旁瓣约束情况下的优化结果。仿真参数为：阵元关于阵列中心对称分布，阵元均为理想的全向性天线单元，栅格间距d=0.5 λ，逆FFT与FFT运算点数K=16 384，迭代循环总次数Num=1 000次。
3.1 仿真结果
　 (1) 阵列大小为1 000，稀疏率为80%，旁瓣约束为 －33.0 dB的大型直线稀疏阵列优化结果如图2所示，得到的最优PSL为－21.28 dB。

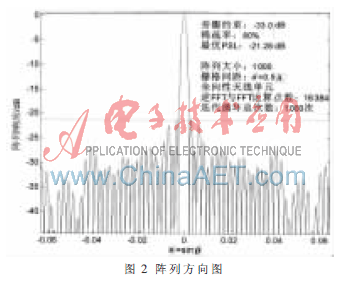
    (2) 阵列大小为1 000，稀疏率为77%， 旁瓣约束为－32.4 dB的大型直线稀疏阵列优化后,得到的最优PSL为－23.21 dB。
　 (3) 阵列大小为1 000， 稀疏率为66%, 旁瓣约束为－31.4 dB的大型直线稀疏阵列优化结果如图3所示，得到的最优PSL为－27.39 dB。

　通过对上述仿真结果的观察和比较可以发现，得到的大型直线稀疏阵列优化结果是符合阵列优化规律的，即在优化阵列中，阵元的稀疏总是发生在阵列边缘，而阵列中心的阵元一般不会被稀疏掉，并且在一定范围内，稀疏率越小，所得到的最优PSL就越低[5]。
3.2 优化方法的性能分析
　 以上所有仿真均在MATLAB7.1中完成，计算机配置为：AMD Phenom(tm)9650 Quad-Core处理器，主频为2.3 GHz，每次仿真所花费的时间仅为1 min左右。图4为仿真实验（3）中，优化效果最好、优化效果最差、迭代次数最少和迭代次数最多的迭代循环中的PSL变化情况。从图中可以看出，稀疏阵列经过较少次迭代后，其旁瓣性能就能得到很好的改善。这说明了该优化方法具有高效性。

    表1给出了阵列大小为1 000、稀疏率为66%，旁瓣约束为－31.4 dB的大型直线稀疏阵列20次相对独立的优化结果，其中最好的结果为－27.39 dB，最差的结果为－26.91 dB，最优PSL的平均值为－27.15 dB，方差为0.146 7。结果表明每次优化得到的最优PSL总是在一个很小的范围内变化。这说明了该优化方法具有稳健性。

    迭代FFT算法在解决大型稀疏阵列的优化问题上，有其独特的优势。本文使用迭代FFT算法快速地实现了大型直线稀疏阵列的优化设计，为同类研究提供了有价值的参考。仿真结果证明了该方法的高效性和稳健性。此外，该优化方法还可拓展成2维FFT后应用到平面稀疏阵列的优化设计当中。
参考文献
[1] 王玲玲,方大纲.运用遗传算法综合稀疏阵列[J].电子学报,2003,31(12A):2135-2138.
[2] KEIZER W P M N.Large planar array thinning using iterative FFT techniques[J]. IEEE Trans. Antennas Propagation,2009, 57(10):3359-3362.
[3] 徐振华. 相位锥化低旁瓣和差波束方向图合成新方法[J]. 兵工学报,2011,32(3):286-291.
[4] KEIZER W P M N. Linear array thinning using iterative FFT techniques[J]. IEEE Trans.Antennas Propagation,2008, 56(8):2757-2760.
[5] 陈客松,何子述,唐海红.对称线阵的优化稀疏研究[J].电子与信息学报,2009,31(6):1490-1492.
[6] Chen Kesong, He Zishu, Han Chunlin. A modified real GA for the sparse linear array synthesis with multiple constraints[J]. IEEE Trans. Antennas Propagation, 2006,54(7):2169-2173.