多输入多输出MIMO（Multiple-input Multiple-Output）和正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)技术相结合，能克服无线传输的频率选择性衰减问题，并提高通信系统的容量和频谱利用率。而在分集接收、相关检测、解码等信号处理中需要知道信道的特性，因此，在MIMO-OFDM系统中，信道估计器是至关重要的。在MIMO-OFDM系统中，信道估计器的技术应用研究主要集中在基于导频的方法上[1]。在基于导频的方法中，已知的导频符号可以在一些特定的子载波上或时隙上传输。在接收端，根据接收的导频点信号可以估计出导频点对应的频率或是时间上信道的特性，从而重建整个信道的特性。等间隔的导频间隔设计是性能最稳定的方案，且在信噪比较大和信道相关矩阵满秩的情况下，此设计方案是最优的[2]。参考文献[3]研究在时变衰落信道中，如何设计导频间隔，以保证低于一定的平均误码率，参考文献[4]研究在保证传输中时间间隙最大条件下，最佳导频数据的长度和间隔。参考文献[5]研究使未编码传输系统最大误码率最小时，所对应的导频点个数。这些研究的条件都是小多普勒频移和大信噪比。针对此问题，本文主要研究信道的相干带宽、多普勒频移和信噪比为不同值时，对最优导频间隔设计的影响，以确定在满足误码率小于一定值的情况下最大的导频间隔，以提高系统的容量。

1 系统描述
     图1描述了有Nt个发送天线和Nr个接收天线的MIMO-OFDM系统模型[6]。在发送端，对二进制数据进行一定的调制，比如QPSK、16QAM、64QAM等。对调制后的数据再进行串并转换，组成K维向量。系统子载波总数假设是N,则有N-K个导频子载波被插入到调制之后的数据中，组成长度为N 的频域数据Xi，其中 i为发送天线标号。将Xi进行逆傅里叶变换,变换成时域的信号xi(n)，再插入循环前缀构成向量xgi(n)。通过并串变换，xgi(n)从第i个发送天线传输到无线信道中。

    每对发送和接收天线之间的信道建模为离散信道，

　
4.1 不同相干带宽的信道的最优导频间隔设计
    图4~图6比较了PA、PB、VA 三种信道中LI、SOI、SCI 三种信道估计器不同的导频间隔对应的误码率性能。该性能的比较是在信噪比为15 dB、多普勒频移为100 Hz条件下的进行的。随着导频间隔的增加，误码率是增加的。根据公式(4）可计算出PA信道中导频间隔的最大值为75，PB的为8，VA的为1。但从图5可看出PB信道下，信道估计器要有效果，即误码率低于没有估计器的误码率所需的最大导频间隔为15，图6说明VA信道下所需的导频间隔是7，比计算出的理想值要大。这是因为信道估计器引入了频率上的相关性，从而使需要的导频数变小，导频间隔增大。而且要达到相同误码率性能，VA信道下的估计器比PA、PB信道下需要更小的导频间隔。所以相干带宽越大的信道，达到一定误码率的导频间隔就越大。

4.2  不同多普勒频移下的导频间隔的设计

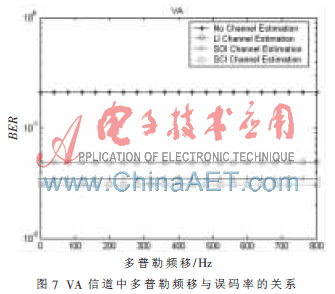
    图7说明VA信道下三种信道估计器对应多普勒频移不同时的误码率性能。此实验是在信噪比为15 dB，导频间隔为7条件下进行的。从结果可看到对于所有的估计器，不同的多普勒频移下误码率是不变的。因此，说明最优导频间隔的选择与多普勒频移无关。同时也说明，对于高速运动中的通信，导频子载波的分布方式是最好的选择。而且，这一结论也适用于其他具有不同相干特性的信道。

4.3 不同信噪比时导频间隔的设计
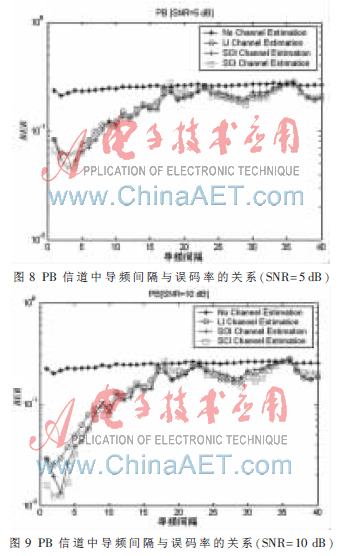
    图8~图10比较了在高信噪比和低信噪比下，不同导频间隔对应的误码率。图10说明,在高信噪比下，随着导频间隔的增加，误码率基本是线性增加的。但图8~图10说明,在信噪比低的情况下，误码率并不是随着导频间隔增加而单调上升的，因此最优导频间隔并不是最小间隔。这是因为噪声恶化了估计器性能。在插值估计算法中，噪声被平均到导频间隔对应的子载波上，因此随着导频间隔的增加，噪声的恶化影响越小。但是之前分析，随着导频间隔的增加，数据的相关度越小，估计性能越差，因此二者折中后，必存在一非最小值的最优导频间隔。

    本文研究了基于导频子载波的MIMO-OFDM系统的最优导频间隔的设计问题。对于LI、 SOI、 SCI三种插值信道估计器，研究信道相干带宽、多普勒频移、信噪比对于最佳导频间隔设计的影响。信道相干带宽越大，达到相同误码率性能所需的导频间隔就越大，因此在一定误码率性能的约束下，选取最大的导频间隔可以提高系统的容量。多普勒频移对子载波导频方案的导频间隔选取是没有影响的，因此在快速运动通信中，子载波导频方案是一个不错的选择。研究发现，在信噪比低的时候，最优导频间隔并不是最小导频间隔，因此存在使得误码率最低的最优导频间隔，其值不为最小值，从而在系统容量和误码率权衡下有一相对最佳的导频间隔。
参考文献
[1] 袁静，高永安. MIMO-OFDM系统信道估计中的最优导频设计[J].电子技术应用,2011,37(1):98-101.
[2] SAVAZZI S, SPAGNOLINI U. On the pilot spacing constraints for continuous time-varying fading channels[J]. IEEE Transactions on Communications, 2009,57(11):1-5.
[3] LI Y, WINTERS J H, SOLLENBERGER N R. MIMO-OFDM for wireless communications, signal detection with  enhanced channel estimation[J]. IEEE Trans. Commun., 2002,50(9):1471-1477.
[4] SAVAZZI S, SPAGNOLINI U. Optimizing training lengths and training intervals in continuous time-varying fading  channels[J]. IEEE Trans. Signal Processing, 2009,57(3).
[5] DONG M, TONG L, SADLER B M. Optimal insertion of  pilot symbols for transmissions over time-varying flat fading  channels[J]. IEEE Trans. Signal Processing, 2004,52(5):1403-1418.
[6] SHIN M, LEE H, LEE C. Enhanced channel-estimation technique for MIMO-OFDM systems[J].IEEE Trans.Vehic.Tech., 2004,53(1):261-265.
[7] VITHANAGE C, CEPEDA R, COON J, et al. MIMO-OFDM pilot placement algorithms for wideband indoor communications[J]. IEEE Transactions on Communications, 2011,59(2):466-476.
[8] SPETH M. Optimum receiver design for OFDM-based broad-band transmission-Part II: a case study[J]. IEEE Transactions on Communications, 2001,49(4):571-578.
[9] 3GPP TS 36.211. Physical channels and modulation[M]. Technical Specification Group Radio Access Network (Release 8).