基于电压岛的动态电压频率缩放DVFS(Dynamic Voltage and Frequency Scaling)技术能够大幅度地降低片上网络NoC(Network on Chip)的能耗,从而受到广泛关注[1]。在基于电压岛的NoC上，电压和频率的改变以整个电压岛为单位，DVFS设计需要全面考虑电压岛内所有的IP核。与针对单个IP核的DVFS控制算法相比,基于电压岛的DVFS控制算法需要考虑的因素更多，设计也更为复杂。

    目前,针对基于电压岛的DVFS控制算法的研究并不多。为了应对工作负载的快速变化，参考文献[2]提出一种基于全局电压岛输入队列使用率的反馈控制算法。该算法使用反馈控制，较好地应对了工作负载的变化。而参考文献[3]指出参考文献[2]的控制算法逻辑资源消耗过高，缺乏全局控制，在参考文献[2]的基础上提出CF-g反馈控制算法，该算法利用片上的g个输入队列,实现了电压岛简单、高效的工作电压控制，达到了资源和效率的平衡，但是该算法并没有大幅度降低片上逻辑资源的开销。同时，参考文献[2]和参考文献[3]的算法存在的共同问题是只能控制电压岛的一个输入队列，导致整个系统的稳定性较差。
    针对上述问题，本文依据参考文献[4]提出的输入队列包到达模型提出一种基于岛间队列特征的DVFS控制算法。该算法使用电压岛的所有输入/输出队列参与电压岛的电压/频率控制，提高了片上通信的稳定性，引入岛间队列使用率和增长率进行负载预测，提高了算法的效率。
1 算法设计
1.1 电压岛间队列使用率的数学模型
    在基于电压岛的NoC上，电压岛间的每个链路两端各有一个缓存队列，如图1所示，可将这种缓存队列简称为岛间队列[4]。电压岛VFI1是队列q的输入电压岛，电压岛VFI2是队列q的输出电压岛;相应地，队列q是电压岛VFI1的输出队列，也是电压岛VFI2的输入队列。设队列q的平均包到达速率为f1λ，包服务速率为f2 μ，f1和f2是第k个控制周期内(即[(k-1)T，kT))两个电压岛的频率，队列q的使用率q(k)∈[0,1]可表示为：
　　

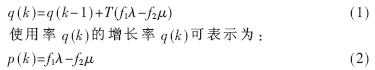
    岛间队列增长率直接指示了当前队列使用率的变化：当p(k)>0时，增长率为正，这时使用率q(k)增加，即队列中待处理的数据包增加；当p(k)<0时，使用率负增长，此时的使用率减小，即队列中待处理的数据包减少；当p(k)=0时，表示当前队列使用率不变，该队列处于平衡状态。
1.2 算法思想描述
    本文将电压岛的频率和电压划分为几个离散的等级，每次调整将增加或者降低一个等级。为了实现对工作负载的预测，引入岛间队列增长率。另外，岛间队列使用率准确描述了当前队列的使用情况，指示了当前的片上通信状况。本算法综合两者的信息得到当前岛间队列对电压岛的频率需求（升频、降频）。
    针对当前的控制算法无法达到控制所有岛间队列的问题，通过全面考虑电压岛的输入、输出队列对电压岛工作频率的需求，综合全局信息来配置电压岛的电压和频率。在保证通信稳定的前提下尽量降低能耗，对于增频请求和降频请求，依据保证系统通信稳定的原则，优先处理增频请求。
    本算法采用全局控制方式，整体结构如图2所示。设控制周期为T，在第k个控制周期开始时，对各个电压岛的频率和岛间队列的使用率进行采样；然后将采样信息输入全局电压/频率控制模块进行运算,得到当前的岛间队列增长率；之后，由全局电压/频率控制模块依据DVFS控制算法得出各个电压岛在下个周期的电压和频率；最后，由电压/频率生成模块对电压和频率进行转换，电压和频率转换完成后，进入第k+1个周期。

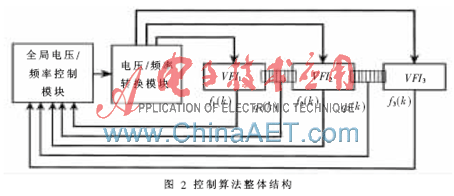
    电压岛的电压和频率采用离散值，算法每次将电压岛的工作频率升高或者降低一个等级。
1.3 使用岛间队列的DVFS控制算法原理
    对于由J个电压岛组成的NoC，假设电压岛i有m个输入/输出队列。本算法根据电压岛的输入/输出队列的使用率q(k)和增长率p(k)来控制电压岛的工作电压,以实现DVFS控制。考虑到输入/输出队列对电压岛工作频率的不同需求，将两者分开考虑，其对应的控制请求可分为输入队列请求和输出队列请求。
    本算法通过综合q(k)和p(k)的信息控制电压岛的频率，使p(k)在区间[0，1)之内变化。其原理如下：
　 在图 1中，对于队列q，当p(k)>0时，若保持电压岛VFI1的频率f1和电压岛VFI2的频率f2不变,则队列的使用率q(k)会持续增加。这种情况下，当q(k)较小时，无需考虑降低频率f2或者增加频率f1；当q(k)较大时，为避免队列拥塞(即防止q(k)=1)，为其设置门限值ThH， 当q(k)到达门限值ThH时，可以降低输入电压岛的频率f1或者增加输出电压岛的频率f2；当使用率q(k)很小时，若降低队列的输出电压岛频率f2，则增长率p(k)>0变大，加快了q(k)增加的速率。为了解决此时能否降低f2的问题，设置了q(k)的可降频门限ThD。当p(k)>0，q(k)<ThD时,可以降低队列的输出电压岛的频率；当增长率p(k)>0时，如果队列的输入电压岛的频率f1将在下一个控制周期被提高，按照式(2)推断增长率p(k)会变大，此时有必要降低输出电压岛的频率f2的门限，令这个门限值为ThI,本文称之为输出电压岛从动升频门限。
    当p(k)<0时，若保持f1和f2不变，队列的使用率q(k)会持续减小，此时不必考虑q(k)过高而导致队列拥塞；当使用率q(k)过低时，可以增加输入电压岛的频率f1或者降低输出电压岛的频率f2。为了降低能耗，本算法不主动增加输入电压岛的频率， 这时设置队列使用率q(k)的门限ThL，当q(k)到达此门限值时，降低输出电压岛的频率；若输出电压岛的频率f2降低，则增长率变大，使用率有可能会增加，此时，若q(k)&isin;[ThH,1]，则不能降低输出电压岛的频率f2；若q(k)&isin;[ThL,ThH），则可以降低输出电压岛频率f2。
    当p(k)=0时，队列的输入输出达到平衡，队列对电压岛的频率没有升降请求。
    本算法的控制方法如表1、表2所示。

    从图3可以看出，本算法的总能耗和CF-g算法相近。在五种应用中，相比于NOP，CF-g算法平均降低了16.19%的总能耗，本文算法平均降低了19.85%的总能耗。本文算法没有获得较大的能耗降低空间，这是由于算法采用了全局控制机制，增加了可控的岛间队列的数量，牺牲了一定的能耗降低空间。从图4的EDP对比中可以看出，本文算法的能耗性能大大提升，相比于NOP，本算法获得了21.82%的性能提高。相比于CF算法，本文算法也有6.14%的性能提高。

    本文提出了一种使用岛间队列的DVFS控制算法，利用岛间队列增长率和使用率两个参数来控制电压岛的电压/频率变化。仿真结果表明，本算法保障了片上通信的稳定性，明显提高了系统吞吐量。
参考文献
[1] Liang Guang, LILJEBERG P, NIGUSSIE E, et al. A review of dynamic power management methods in NoC under emerging design considerations[C]. In:Norchip Conference, 2009. Trondheim, 2009.
[2] OGRARS U Y, MARCULESCU R, MARCULESCU D. Variation-adaptive feedback control for networks-on-chip  with multiple clock domains[C]. New York : Proceedings of  the 45th annual Design Automation Conference,2008:614-619.
[3] GARG S, MARCULESCU D,MARCULESCU R. Custom feedback control:enabling truly scalable on-chip power management for MPSoCs[C]. Austin: Low-Power Electronics  and Design, 2010 ACM/IEEE International Symposium on, 2010:425-430
[4] JUANG P, Wu Qian. Coordinated, distributed, formal energy management of chip multiprocessors[C].Princeton Univ:  Low Power Electronics and Design,2005.Proceedings of the  2005 International Symposium on, 2005:127-130.
[5] DICK R. Embedded system synthesis benchmarks suites(E3S)[EB/OL](2011.12.14).http://www.ece.northwestern.edu.
[6] ERIK B, VAN D T, JASPERS E G T Jaspers. Mapping of MPEG-4 decoding on flexible architecture platform[A]. In: SPIE Conference on Visualization and Data Analysis[C]. San Jose, CA, USA: IEEE, 2002: 1-13.
[7] HOWARD J, DIGHE S, SRIRAM R,et al.A 48-Core IA-32 processor in 45 nm CMOS using on-die messagepassing and DVFS for performance and power scaling[J]. IEEE Journal of Solid-State Circuits, 2011,46(1):173-183.
[8] RAHIMI A, SALEHI M E. MOHAMMADI S, et al. Dynamic voltage scaling for fully asynchronous NoCs using FIFO threshold levels[C]. Tehran: Computer Architecture and Digital Systems,2010 15th CSI International Symposium on, 2010:43-48.