0 引言

　　随着电力电子技术的发展，电力电子装置带来的谐波问题对电网安全、稳定、经济运行带来了极大影响，人们急需能够在电网中对所有谐波参数进行实时准确的检测与分析。电网谐波由于受非线性、随机性、分布性、非平稳性及复杂性等因素影响，对谐波进行准确实时检测非常重要且并非易事，目前人们正在不断探索更为有效的谐波实时检测方法及其实现技术。

　　目前，电网谐波检测" title="谐波检测">谐波检测主要通过谐波电流的检测来实现。谐波检测主要有以下几种方法：(1)采用模拟带通或带阻滤波器" title="滤波器">滤波器检测，(2)基于广义瞬时无功功率的谐波检测法，和瞬时无功功率理论一样，在解决谐波总量实时检测方面很有优势，在谐波实时监测领域有着广泛应用，本文主要是引用该方法进行谐波实时检测。(3)基于傅立叶变换的谐波检测，是当今应用最广泛的一种方法，缺点是检测实时性较差。在稳态谐波检测中大多数采用快速傅立叶变换及其改进算法，而对于波动谐波或快速变化的谐波，则需另寻他法。(4)基于神经网络的谐波检测法，它主要有3方面的应用：①谐波源辨识；②电力系统谐波预测；③谐波检测。(5)基于小波变换的谐波检测法，小波变换是一个时间和频率的局域变换，对波动谐波、快速变化谐波的检测有很大的优越性，也存在固有缺陷，如窗口能量不集中，出现频率叠混现象，缺乏系统规范的最佳小波基选取法等。

　　应用基于广义瞬时无功功率理论算法对谐波电流进行实时检测，利用MATLAB软件搭建立了相应的仿真电路，针对检测电路中的低通滤波器对实时检测效果的影响进行了仿真分析，分析了低通滤波器LPF的类型、截止频率fc和阶数n选取，对基于广义瞬时无功功率理论的谐波实时检测电路的动态响应过程有重要影响。

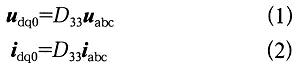
　　由abc坐标系至dq0坐标系的线性变换矩阵为

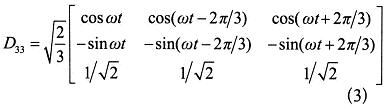
　　将dq0坐标系下的电流向量idq0分解为相互正交的两个分量，

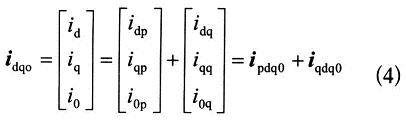
　　其中，电流矢量ipdq0和电压矢量Udqo在同一坐标轴上。

　　设三相四线制电路中电流含有正序分量、负序分量、基波和各次谐波零序分量，如下式所示：

　　上式中下标1m为第m次正序电流，下标2m为第m次负序电流，下标0m为第m次零序电流。

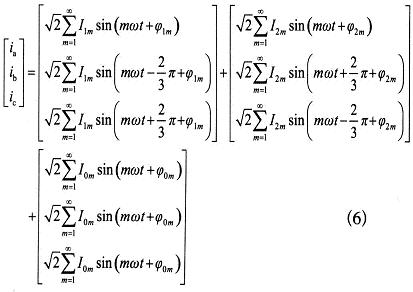
　　其中，id和id分别为id的直流分量和交流分量，iq和iq分别为iq的直流分量和交流分量，如下式所示：

　　id、iq经低通滤波器得到直流分量id、iq，i0经带通滤波器提取其中的负载基波电流i0'：

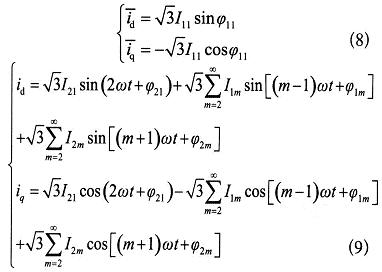
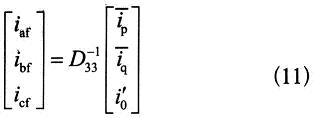
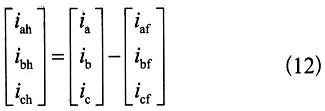
　　可见d轴电流直流分量id与负载基波正序有功分量相对应，q轴电流直流分量iq与负载基波正序无功分量相对应，d轴电流交流分量id和q轴电流交流分量id分别与高次谐波的有功分量和无功分量相对应，故id和i0经LPF后即得到与基波对应的正序有功分量和正序无功分量。0轴分量经带通滤波器后与负载基波不对称分量相对应。因此则可得基波电流表达式为：

　　则系统谐波电流就可检测出来：

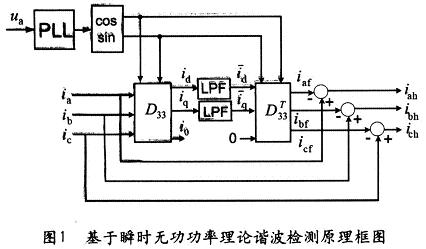
　　基于瞬时无功功率理论谐波检测理论，本文应用的谐波实时检测电路框如图1所示：

　　2 低通滤波器在谐波实时检测中的应用

　　在所有基于瞬时无功功率理论的谐波和基波无功的检测方法中，都要用到低通滤波器。低通滤波器用于从总的有功电流和无功电流中获取其直流电流分量，再由直流分量通过PARK反变换获得基波电流，进而获得要检测的谐波电流。显然，低通滤波器的性能直接检测对系统检测的动态跟踪速度起着重要作用，最终影响有源电力滤波器的谐波检测实时性，由此看出低通滤波器的设计是非常重要的环节。

　　针对谐波检测的实时陛要求，本文在检测方法中用数字低通滤波器来代替传统的模拟低通滤波器。数字低通滤波器相对于模拟滤波器史容易进行数学运算，能有效地克服模拟滤波器所无法克服的电压漂移、温度漂移及时间漂移等问题，实现近似的理想响应和线性的相位，能更好达到谐波检测的实时性的要求。

　　通过理论分析和仿真比较，采用二阶巴特沃斯低通数字滤波器，建立谐波检测的Simuliuk仿真模型。

　　1)ButterWorth低通滤波器设计

　　Butter Worth低通滤波的传递函数可以表示为(数字滤波器)

　　n为滤波器的阶数，在MATLAB的信号处理工具箱SignalProcessing Toolbox里设计2阶Butter worth低通滤波器。MATLAB的信号处理工具箱提供了有关巴特沃斯滤波器的函数buttap，buttord，butter。调用butter设计函数就可设计出满足性能指标的巴特沃斯滤波器。

　　理论分析，截止频率越小，谐波电流检测精度越高，动态响应过程越慢，截止频率取得大，可以加快检测电路的动态响应时间，但有部分低次谐波不能被LPF衰减掉，谐波电流检测精度不好。因此，实际谐波电流检测电路中，截止频率既不能选得太小，也不能选得太大，在谐波实时检测电路中，特别要注意谐波电流检测电路的动态响应。这次设计出低通滤波器采用二阶Butterworth低通滤波器，截止频率选取为f=30Hz。

　　巴特沃斯滤波器在线性相位衰减斜率和加载特性二个方面具有特性均衡的优点，因此在实际使用中，巴特沃斯滤波器己被列为首选。通过理论分析和仿真比较，采用二阶巴特沃斯低通数字滤波器，建立谐波检测的Simuliuk仿真模型。显而易见，采用数字低通滤波器时，动态响应过程比采用模拟低通滤波器实时性好，且检测的结果也更为准确。

　　设计出的数字低通滤波器的电路仿真曲线见图2和图3。

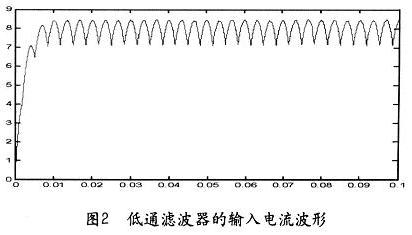
　　3 结束语

　　本文通过基于瞬时无功功率理论的谐波电流检测方法，借助于MATLAB软件包中SIMULIMK" title="SIMULIMK">SIMULIMK工具箱，搭建谐波实时检测电路仿真模型，并设计了合理的二阶butterwortn低通滤波器，对在检测电路中用到的低通滤波器对谐波电流检测效果的影响作了仿真研究。特别针对低通滤波器在谐波实时检测中的应用所要注意的低通滤波器设计参数，如截止频率和阶数对检测实时性的影响做了实际研究，为以后的谐波实时检测电路设计提供有益参考。