引言

　　在各类电子系统中，数字电路所占比重越来越大。这主要是因为数字电路相对于 电路有一些突出的优点，例如：1 数字电路中的有源器件工作在饱和区 与截止区，工作状态稳定；2 数字电路处理的是二值信号，易于存储和再生；3 数字电路是由大量相同的基本单元，如门、触发器等所组成，易于大规模集成，易于自动化设计工具的应用等。再加上数字计算机和数字信号处理技术的迅速发展，使得数字电路从集成规模、应用范围及设计自动化程度等方面都大大超过了模拟电路，越来越多的由模拟电路实现的功能转由数字电路实现，进入了电子系统设计的数字化时代。

　　1  变∑-Δ换的原理

　　∑-Δ变换采用过取样技术，将信号按时间分割，保持幅度恒定，具有高取样率、噪声整形和比特字长短的特点。变换可以在低取样率、高分辨率的量化器或者高取样率、低分辨率的量化器中进行，在数字音频中很有用，如用于音频信号数字化的∑-Δ ADC及可将已经数字化处理后的音频信号还原为模拟声音信号的比特数时所带来的量化非线性误差、纠错困难的缺点。

　　∑-Δ变换是将信号按时间分割，保持信号幅度恒定。它用高电平或低电平的脉冲表示信号，例如可以采用脉冲密度调制（PDM），如图1所示恒定幅度的脉冲信号，不论电平高或低都能够重建输出信号波形。　　打个比方来说明如何用1比特替代16或更多比特：传统的阶梯变换器像16个电灯泡，连接到各自的开关上，每个都有不同的亮度，用各种组合方式可以得到216（即65536）种不同的亮度。然而，灯泡间的亮度差会引入误差，某种组合也并不总是能够产生所要求的亮度。1比特变换技术采用完全不同的方法，不用那么多灯泡和开关，只用一个灯泡和一个开关。房间亮度的变化可以通过简单的改变开、关灯泡的次数来得到。如果灯泡开的次数增加，房间的亮度就会增加。

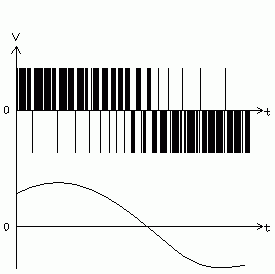
 图1 脉冲密度调制

　　2  ∑-Δ DAC的结构

　　传统的应用电流模技术的DAC当位数达到10位以上时，要在某一温度范围保持精度非常困难。本文的∑-Δ DAC运用了数字技术，因此与电流模DAC相比，不受温度变化的影响，且能在可编程逻辑器件如FPGA" title="FPGA">FPGA中实现。∑-Δ DAC实际上是高速1位DAC，应用数字反馈技术从输入二进制数字量产生等幅的脉冲串，脉冲串的平均占空比与输入二进制数字量成正比，脉冲串再通过一RC模拟低通滤波器就能重建模拟波形。∑-Δ DAC非常适合于低频、高精度的应用，尤其在数字音频领域应用广泛。

　　作为例子，本文中所描述的∑-Δ DAC的二进制8位输入数字量是无符号数，模拟输出电压值都是正值。输入“00000000”产生输出电压0V，“11111111”产生输出电压的最大值Vmax，Vmax非常接近VCCO，其中VCCO是FPGA芯片I/O端口的供电电压。         

∑-Δ DAC" title="∑-Δ DAC">∑-Δ DAC的内部结构图 " border="0" height="319" hspace="0" src="http://files.chinaaet.com/images/20100811/1130b331-9554-44dd-af03-bba3467f2219.jpg" style="WIDTH: 577px; HEIGHT: 319px" width="577" />

　　图2  ∑-Δ DAC的内部结构图    

       术语“∑-Δ”分别代表算术和与差，都可用二进制加法器来产生。虽然Δ加法器的输入是无符号数，但Δ和∑两加法器的输出被看作有符号数。Δ加法器用来计算DAC输入与当前DAC输出之间的差值。由于DAC的输出只有一位，非0即1，即全0或全1。如图2 ∑-Δ DAC的结构图所示，Δ加法器的另一个输入值由∑锁存器最高位L[9]的两个拷贝后面跟8个0产生，这也弥补了DAC输入值是无符号数的问题。∑加法器将它的上一次输出（已经保存在∑锁存器）与Δ加法器的当前输出求和。

　　3 ∑-Δ DAC的FPGA实现

　　如图2所示，∑-Δ DAC的内部仅由2个10位的二进制加法器，1个10位的锁存器和一个D触发器组成，用FPGA实现时只需耗费极少的逻辑资源，即使用最小的FPGA也能实现，本文采用了Xilinx Virtex" title="Virtex">Virtex FPGA，图3给出了FPGA实现的顶层原理图。输入信号有8位宽的二进制数字量DACin[7:0]、时钟信号CLK和复位信号Reset；输出信号为等幅脉冲串DACout，通过一个驱动缓冲器OBUF_F_24（是Xilinx FPGA特有的SelectI/O资源，OBUF表示输出缓冲器，F表示它的转换速率快，24表示它的驱动能力即输出驱动电流是24MA，基于LVTTL I/O标准）驱动FPGA外部的模拟RC低通滤波器，该缓冲器的输出端连接到FPGA的I/O端口，则它的驱动电压即为FPGA的I/O端口的供电电压VCCO。表1列出了∑-Δ DAC的接口信号。

　　图3  FPGA实现∑-Δ DAC的顶层原理图

　　表1  ∑-Δ DAC的接口信号    

　　图3虚线框内的电路都在FPGA里面实现，其中的DAC模块的原理图见图2，在本文中是用可以综合的VerilogHDL" title="VerilogHDL">VerilogHDL语句来描述的。VerilogHDL描述的可综合性是指其可被综合工具所识别，将其寄存器传输级（RTL）描述综合成门级网表，最终能通过FPGA的布局布线工具映射到FPGA当中成为能完成指定功能的硬件电路。VerilogHDL语言最初是面向建模和仿真的，只有10%可以被综合称为可综合子集。对于不同的综合工具，可综合子集的内容并不相同。IEEE的一个工作组目前正在撰写一个名为IEEE Std 1364.1RTL的综合子集的规范，定义了一个最小的可综合的Verilog语言要素的子集，以便得到各综合工具提供商的支持。

　　图3中缓冲器的输出端DACoutDrvr连接到FPGA的输出引脚上，驱动外部的模拟RC低通滤波器。图

中R=3.3kΩ，C=0.0047μF，VOUT即为最终转换所得的模拟信号。下面给出了DAC模块的可综合的VerilogHDL描述：

　　‘timescale 100 ps / 10 ps

　　//This is a Delta-Sigma Digital to Analog Converter

　　module dac(DACout, DACin, Clk, Reset)；

　　output DACout； // This is the average output that feeds low pass filter

　　reg DACout；

　　input [7:0] DACin； // DAC input

　　input Clk；

　　input Reset；

　　reg [9:0] DeltaAdder； // Output of Delta adder

　　reg [9:0] SigmaAdder； // Output of Sigma adder

　　reg [9:0] SigmaLatch； // Latches output of Sigma adder

　　reg [9:0] DeltaB； // B input of Delta adder

　　always @(SigmaLatch) DeltaB = {SigmaLatch[9]，SigmaLatch[9]} << (8)；

　　always @(DACin or DeltaB) DeltaAdder = DACin + DeltaB；

　　always @(DeltaAdder or SigmaLatch) SigmaAdder = DeltaAdder + SigmaLatch；

　　always @(posedge Clk or posedge Reset)

　　begin

　　if(Reset)

　　begin

　　SigmaLatch <= #1 1’bl << (8)；

　　DACout <= #1 1’b0；

　　end

　　else

　　begin

　　SigmaLatch <= #1 SigmaAdder；

　　DACout <= #1 SigmaLatch[9]；

　　end

　　end

　　endmodule该程序经过Xilinx的FPGA集成开发工具ISE6.2编译（含综合过程）、仿真后，再选择Virtex系列FPGA芯片进行配置。设置CLK=100MHz（最高可达219MHz）。

　　4 结论

　　∑-Δ DAC是高速FPGA芯片用于数字模拟混合信号系统设计的尝试，可应用于可编程电压源、波形发生器、声音发生器、RGB颜色发生器和ADC的参考电压发生器等，极大的减少了系统的元件数目，降低了系统的成本，有很好的实用价值。

　　参考文献

　　[1] （美）巴斯克尔著，孙海平译《VerilogHDL综合实用教程》，清华大学出版社，2004

　　[2] 王诚，薛小刚《FPGA/CPLD设计工具：Xilinx ISE5.x使用详解》，人民邮电出版社，2003

　　[3] （美）Ken C.Pohlmann著，苏菲译《数字音频原理与应用》第四版，电子工业出版社，2002

　　[4] www.xilinx.com，Xilinx公司在线文档