摘 要: 针对传统的缺陷定位必须经过图像分割和缺陷提取等步骤,识别过程比较麻烦而且费时,提出了一种基于分块分形的工业CT图像缺陷自动定位算法。该方法首先对图像进行分块处理,对每个分块区域进行分形维数计算。通过分形维数频域分布直方图进行阈值处理,标记边缘块,最后通过连通区域处理标记块,进而对缺陷进行标记定位。通过对含有不同缺陷数目的固体火箭发动机模型工业CT图像处理,均可以准确地定位缺陷。实验结果表明,该方法能有效、准确地自动定位工业CT图像缺陷,且具有较强的鲁棒性。
关键词: 缺陷定位;分形;工业CT;分块;区域连通
0 引言
计算机断层扫描成像技术(Computed Tomography),简称CT[1],作为现代无损检测技术的重要组成部分,越来越受到人们的重视。工业CT是CT技术在工业领域的应用,主要是为了工业产品的内部成像和缺陷检测,是目前最为精确可靠的无损检测技术之一[2]。缺陷的自动定位是工业CT实现无损检测的重要组成部分,传统的图像缺陷定位一般要经过图像分割、特征提取等过程[3],定位过程比较麻烦而且计算量大,如果能对图像进行自动定位[4],对缺陷区域进行针对性处理,就可以减小图像分割的计算量,甚至在一些情况下只需知道缺陷的位置,无需图像分割。为此,本文通过采用分形理论,直接自动定位图像的缺陷,无需进行图像分割过程,降低了计算量,大大节省了时间开销。
1 分形理论
1.1 分形和分形维数
分形理论是近年发展起来的数学工具,它是美籍法国数学家Mandelbrot在20世纪80年代中明确起初的[5],其研究对象是自然界中常见的、不稳定的、不规则的现象,天空的云彩、不规则的海岸线都是很好的例子。目前关于分形并没有明确的数学定义[6],Mandelbrot曾尝试给出一个定量刻画,说Hausdorff Besicovitch维数严格大于拓扑维数的集合称为分形, 然而这只是试验性的定义,不够全面和精确,也没有可操作性。目前流行的对分形的表述定义为:一般地,如果F满足以下定义,则称它是一个分形[7]。
(1)F具有精细的结构,即有任意小比例的细节;
(2)F是如此不规则,以至于它的整体与局部都不能用传统的集合语言来描述;
(3)F通常具有某种自相似性,近似的或者统计上的;
(4)一般地,F的“分形维数”(以某种方式定义的)大于它的拓扑维数;
(5)F的定义常常是非常简单的,或者是递归的[8]。
分形作为一个数学集,其内部应具有精细的结构[9],也就是在所有比例尺度上其组成部分应包含整体,而且是自相似的,它以其独特的手段来解决整体与部分的关系问题。分形表述的是自然界中的无特征长度的、极不规则的、极不光滑的、维数不一定为整数的对象[10]。分形维数作为刻画分形的不变量,定量地刻画了这种不规则性的程度。具体应用到图像上时,图像边缘灰度变化剧烈,分形维数数值较大。平滑的区域灰度变化缓慢,分形维数较小。
1.2 Blanket方法
Pentland假定,如果一个物体的表面是分形的,则由它产生的图像灰度表面也具有分形的性质,反之亦然。因此,可以从灰度图像中提取分形维。Peleg在分形布朗随机模型的基础上,基于图像表面的灰度信息创立了“双毯法(Blanket)“。设g(i,j)为图像的灰度函数,Blanket方法想象有一个毯子覆盖图像的灰度曲面,设毯子的上表面为Uδ(i,j),下表面为Bδ(i,j)。取一组尺度{δ|δ=1,2,…,N},定义不同尺度的上下表面如下:
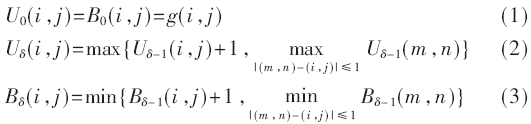
通过以上式子可以获得上下表面积的数值,通过上下表面积的差值即可求得体积,然后根据面积和体积的关系计算获得分形面积Aδ,根据明可夫斯基定义,分形面积A?啄和分形维数D有如下关系:

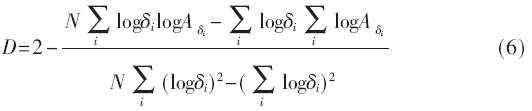
2 分块分形算法
根据分形理论,可以知道在灰度图像的边缘处图像的分形维数会比图像其他位置的分形维数大。所以可以将整个图像分成大小相等的若干矩形块,对每个块进行分形维数计算,通过设定一个分形维数阈值,将大于该阈值的块认定为存在图像边缘。最后通过连通区域计算,将正常的工具边缘去除,提取图像的缺陷。
2.1 缺陷自动定位算法
通过以上的分析,可以通过计算各个分块的分形维数来进行缺陷的自动定位。因此,缺陷自动定位算法是由以下步骤构成的:
(1)将图像分成若干个相等的矩形区域;

(3)根据式(6),利用最小二乘法拟合直线可以求得分形维数D。
(4)块标记:设定一个分形阈值K,将分形维数大于该阈值的分块认定为其内部存在边缘。对存在边缘的块的边界进行白色标记,图1是一个大小为352×352的包含两个孔洞缺陷的固体火箭发动机模型工业CT原始图像,图2是对图1进行块标记结果。


(5)由于块标记中的块可能是工件的边缘或者缺陷区域,通过分析可知,缺陷区域标记的块数目明显小于正常工件边缘。所以本文对标记图像中的标记块进行连通区域分析,计算块标记图像中各个连通区域块的个数,如果连通块数量大于预先设定的连通阈值T,则认为是正常工件边缘。
(6)根据连通区域数目对存在缺陷的工业CT图像进行重新标记,只标记出图像中的缺陷体。图3是对图2的存在两个缺陷的固体火箭发动机模型进行的重新标记。

2.2 算法重要参数
(1)块大小:如果块太小则会导致分形维数的计算不够准确,并且会导致计算量增大。另一方面,块太大可能导致工件边缘和缺陷区域被一个块选中,导致后续的缺陷提取困难。由实验确定,块的大小一般设定为缺陷区域面积的四分之一左右比较合适。
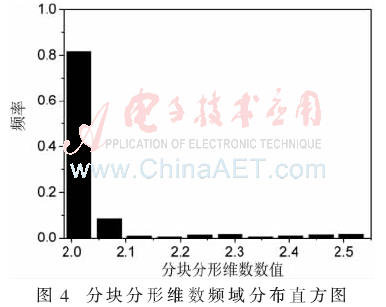
(2)分形阈值K:如果分形阈值K数值设定的过大,则不能完全标记出图像的边缘;相反,如果数值过小,可能将图像背景标记成图像边缘。通过分析分块分形维数的频率分布直方图,可以相对准确地设定分形阈值,因为图像中边缘占据的块相对图像背景占据的块数量较小,在直方图中可以明显看到图像的背景区域的分形维数值。图4是图1按4×4的分块进行分形维数计算后绘制的分块分形维数频域分布直方图,从图中可以直观地看到图像背景区域占据的频率较大,分形维数值在2~2.1之间的频率为0.9左右,因此设定分形阈值K为2.1。图2正是使用该阈值的处理结果,可以看出标记的效果良好。
(3)连通阈值T:为了能准确地将缺陷区域从图像边缘中分离出来,可以根据如下公式选择一个合适的阈值:

其中S1是缺陷区域中面积中最大的一个,S2是分块的面积。
3 实验及结果分析
本实验是在Intel Celeron G1610(双核)2.6 GHz CPU、4G内存的PC上进行的,所用数据为实验室采集并重建的含有人工设计缺陷的固体火箭发动机模型工业CT图像以及从丹东某无损检测公司采集的含有气孔的汽车轮辋X射线图像。
为了验证本文算法的有效性,应用本算法对原始图像图5(a)和图5(c)进行处理,图5(b)和(d)为对应的处理结果。
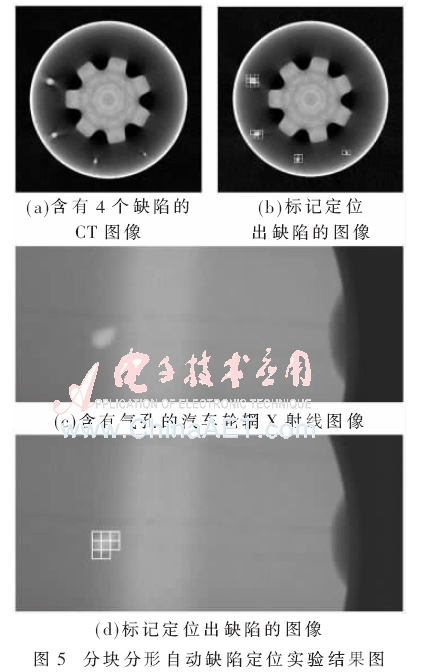
通过分析图5,可以直观地看到图(a)中固体火箭发动机模型中的4个人工缺陷均被准确地定位出来,图(b)中白色边框标记的位置即缺陷所在的位置。图(c)中汽车轮辋X射线图像中的气孔也被正确地标记定位出来,结果如图中(d)所示。实验证明该算法可以比较准确地定位图像中的缺陷,通过自动定位获取的缺陷位置数据,可以方便地进行一些后续的图像处理,如图像分割、缺陷提取、面积计算等。
4 结论
本文围绕工业CT无损检测技术需求,提出了一种基于分块分形的工业CT图像缺陷自动定位算法,该方法将结合分形理论和区域连通原理,可以准确地将工业CT图像中的缺陷体提取出来,具有较强的鲁棒性。
实验证明,该方法简单有效,无需进行图像分割,计算量小。该方法改变了传统的缺陷检测必须先经过图像分割以及特征提取,通过先定位缺陷区域,根据需要可以对局部进行传统的图像处理,可以获得更为准确结果。
参考文献
[1] 蒲云.基于分形维的工业CT图像缺陷自动定位与剥离显示算法研究[D].重庆:重庆大学,2009.
[2] 郭海燕.图像分割算法研究及在工业CT中的应用[D].重庆:重庆大学,2009.
[3] 冷帅,张丽,陈志强,等.CT图像中缺陷的快速定位方法[J].中国体视学与图像分析,2003,8(2):105-107.
[4] 于光辉,卢洪义,朱敏,等.基于标准固体火箭发动机CT结构图像配比的缺陷自动提取方法[J].固体火箭技术,2012,35(3):423-426.
[5] 柴黎.基3D-IC的固体火箭发动机缺陷定位与特征提取技术[D].太原:中北大学,2007.
[6] 曾理,蒲云,马睿.基于工业CT的铁路货车铸件缺陷自动检测[J].中国铁道科学,2009,30(4):76-80.
[7] 李彩霞,李芬华,刘敏.基于分形和神经网络的B超图像识别[J].河北大学学报(自然科学版),2004,24(5):536-540.
[8] 肯尼斯·法尔科内.分形几何-数学基础及应用[M].吉林:东北大学出版社,2001.
[9] MANDELBROT B B.The fractal geometry of nature[M].New York:W.H.Freeman and Company,1983.
[10] 谢永华.基于分形理论木材表面缺陷识别的研究[D].哈尔滨:东北林业大学,2006.

