摘 要: 通过比较几种图像直方图均衡化的应用范围,提出一种基于模糊聚类分割的累计直方图均衡化的方法。实验结果表明:与传统直方图均衡化算法相比,使用该方法处理后的图像不仅使灰度值分布更加均匀,增强了整体对比度,而且保留了原图像更多的细节信息,很好地达到了图像增强的目的。
关键词: 模糊聚类分割;累计直方图均衡化;图像增强
0 引 言
在数字图像处理中,如果图像的灰度分别集中在较窄的区间,则会引起图像细节的模糊。为了使图像细节清晰,并使一些目标得到突出,达到增强图像的目的,可通过改善各部分亮度的比例关系,通过直方图的方法来实现[1]。直方图均衡化又称直方图平坦化[2],是将一已知灰度概率密度分布的图像,经过某种变换,生成一幅具有均匀灰度概率密度分布的新图像,其结果是扩展了像素取值的动态范围,从而达到增强图像整体对比度的效果。
设一幅图像总像素数为n,分为L个灰度级,nk代表第k个灰度级rk出现的频数,则第k个灰度级出现的概率为:
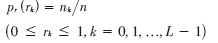
此时变换函数可表示为:
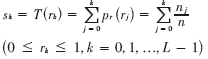
因此,根据原图像的直方图统计值就可算出均衡化后各像素的灰度值。按上式对遥感图进行均衡化处理时,直方图上灰度分布较密的部分被拉伸,灰度分布稀疏的部分被压缩,从而使一幅图像的对比度在总体上得到很大的增强[2]。
目前直方图均衡化常用的方法有直方图扩展(Histogram Expansion)、全局直方图均衡(GHE)、累积分布函数变换法。研究和比较这些方法的优劣,为研究DSP的实现提供比较好的方法。
直方图扩展法[3]使图像得以简化,并且对比度增强。但是,当图像中的灰度值彼此离散时,这种方法就不再适用了。全局直方图均衡(GHE)虽然对于灰度分布较集中的低动态范围图像的增强效果显著,但对于高动态范围图像效果却不明显,有时还会造成小目标以及高频细节信息的丢失。另外,当图像的灰度分布过于集中时,容易造成水渍效应(washed-out effect)。累积分布函数变换法[4]可使图像变得清晰,但是涉及到直方图均衡化时会遇到图像中像素个数较少的灰度级被过多合并的问题,结果导致处理后的图像部分细节丢失而局部变得模糊,得不到满意的增强效果。
本文通过比较各种方法的优缺点,提出了一种基于模糊聚类的累积直方图均衡化的图像处理方法,即利用模糊C-均值聚类算法对图像进行分割,对分割图像的边缘增强,结合累积分布函数变换,对图像进行直方图均衡化,通过双增强,得到图像的高对比度。不同的直方图均衡化所达到的对比度不同,突出图像细节的明显程度不同。本文提出的方法使各种灰度图像(医学图像,指纹图像,人脸图像)有更好的对比度,更能突出图像的细节。
1 一种基于模糊聚类划分的累积直方图均衡化
1.1 模糊C-均值聚类算法
模糊聚类算法[5]是一种基于函数最优方法的聚类算法,使用微积分计算技术求最优代价函数。分类数给定,寻找出对事物的最佳分析方案,此类方法基于目标函数聚类,称为模糊C-均值聚类。
模糊 C-均值聚类算法(FCM) 是基于目标函数的模糊聚类算法中最为完善、应用最为广泛的一种,是图像分割中较为常用的一种算法。
FCM把n个向量xi(i=1,2,…,n)分为c个模糊组,并求每组的聚类中心,使得非相似性指标的价值函数达到最小。与引入模糊划分相适应,隶属矩阵U允许有取值在0、1间的元素。不过,加上归一化规定,一个数据集的隶属度的和总等于1:

所以FCM的价值函数(或目标函数)就是:
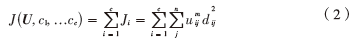
这里uij介于0、1间;cj为模糊组I的聚类中心, missing image file为第i个聚类中心与第j个数据点间的欧几里德距离;missing image file且是一个加权指数。
构造如下新的目标函数,可求得使式(2)达到最小值的必要条件:
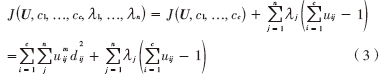
这里λj,j=1,...,n,是式(1)的n个约束式的拉格朗日乘子。对所有输入参量求导,使式(2)达到最小的必要条件为式(4)和式(5):

模糊C-均值聚类分割算法通过将图像的特征数据分成c类来实现图像的分割,通过式(4)和式(5)的迭代确定隶属度和聚类中心,使式(2)所示目标函数取最小值。
经过聚类分割后得到的子块不再是统一的矩形子块,每一个子块都是灰度相近的连通像素的组合,具有相对较窄的灰度分布范围。因此,通过直方图均衡处理后能够得到更好的细节增强能力。
1.2 对二值图像进行图像边缘提取
利用迭代算法得到了图像的二值图像后,可利用该二值图像进行图像边缘提取[6,7]。通过边缘提取后与原图像合并,达到边缘增强的效果。
从二值图像中提取图像的边缘较为方便,对图像中黑色或白色区域中每一个像素的四邻域进行判断即可判断该像素是区域内点还是边缘点。通过边缘检测,文中算法在局部对比度增强和噪声控制方面都取得了较好的效果。
1.3 基于模糊聚类分割的累积直方图均衡化算法
累积分布函数变换法[8]通过统计图像各灰度级像素数量来求得图像直方图信息,并以累积分布函数变换法为基础进行灰度映射,从而很好地增强了图像的整体对比度,达到了使图像更加清晰的目的。
在本文中,选择累积直方图均衡化是因为此方法应用在DSP的实现中具有良好的性能,利用C语言也能很容易实现,为编程者提供了方便。
对图像进行分割之后,对每个子块进行直方图均衡处理,这需要计算累积分布函数,函数定义为:
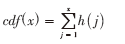
其中x是一个灰度值,h是图像的直方图。
直方图均衡化的一般方程式是:
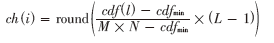
cdfmin是累积分布函数的最小值,M、N是图像的列数和行数,L是灰度级数(在大多数情况下为256)。
2 实验结果及分析
本方法的实现和测试使用的是MATLAB 7.X版本。
本文实验的原始图像及其直方图如图1所示。

从图1可以看出,原图的直方图多密集在一起,这说明图像绝大多数像素点的灰度值比较集中,使得图像信息不够丰富,图像结构不够清晰。下面利用模糊C-均值聚类算法对图像进行分割处理,结果如图2所示。

直方图均衡化算法对于子块的大小比较敏感,当子块较小时,图像的局部对比度较高,同时噪声放大现象也较明显;而子块较大时,又会造成细节丢失。本文取Block size=12来对图像进行直方图均衡化。

利用迭代算法得到图3所示为边缘提取后的图像。图像的二值图像后, 可利用该二值图像进行图像边缘的提取。
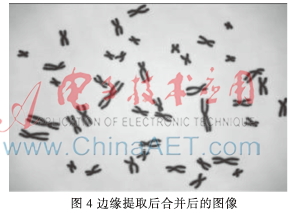
图4即为分割块数为12的分割图像经边缘检测后与原图像合并后的图像。
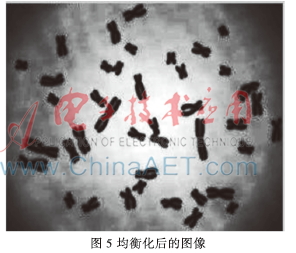
对于分割后的图像利用累积直方图均衡化方法对图像进行均衡化后的结果如图5所示,其直方图如图6所示。
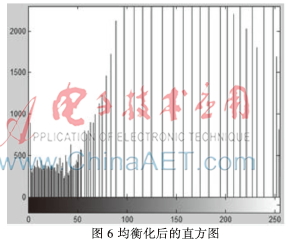
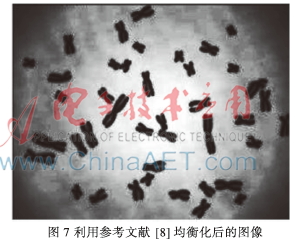
图7为利用参考文献[8]的方法均衡化后的图像。通过计算图5和图7的信息熵,可得图5的信息熵H1=7.953 8,图7的信息熵为H2=7.320 1,利用本文方法均衡化后的熵值明显变大,灰度值分布更加均匀,同时图像也更加清晰,包含更多的有用信息。通过对比图5和图7的信息熵可以得出,利用本文方法不仅很好地扩展了像素取值的动态范围,而且使原来图像中较暗区域中的一些细节更清晰,从而达到了增强图像整体对比度的效果。
3 结论
直方图均衡化技术更适用于黑白色度的图像,如数字x射线图像、指纹图像、人脸图像的增强,便于图像识别。所有这些图片要求很高的清晰度和颜色的对比度。对于由于曝光不均等原因导致的不同位置灰度差异过大的图片,常采用局部阈值分割进行处理。采用局部阈值分割时,分割的结果受图片分块大小的影响。分块时,图片的分块不宜过小,否则每个区块内部的像素过少,统计规律不明显,分割效果不好,且会对背景中的噪声敏感。
参考文献
[1] 姚敏. 数字图像处理[M].北京:机械工业出版社,2006.
[2] 王泽发,唐兴国. 基于灰度变换的图像增强方法研究[J]. 科技创新导报,2011(1):8-13.
[3] Stark J A. Adaptive image contrast enhancement using generalizations of histogram equalization[J]. IEEE Trans actions on Image Processing, 2000,9(5):170-178.
[4] 杨秋霞,曹宗杰. 直方图均衡处理方法的研究[J]. 科技广场,2011(7):11-14.
[5] Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2002 (2):94-101.
[6] 陈冬岚,刘京南,余玲玲.几种图像分割阈值选取方法的比较与研究[J].机械制造与自动化,2003(1):77-80.
[7] 尹平,王润生. 基于边缘信息的分开合并图象分割方法[J]. 中国图象图形学报, 1998(6):1-7.
[8] 吕宗伟,唐治德,周林,等.利用累积分布函数的亮度保持均衡算法[J].计算机辅助设计与图形学学报,2011(9):1-8.

