摘 要: 针对传统的局部线性嵌入算法易受近邻点个数的影响,以及支持向量机的错分点过多对识别率产生的影响,提出了一种基于模糊聚类的局部线性嵌入和支持向量机的人脸识别方法。利用改进的算法对人脸库中的图像进行特征提取,然后采用支持向量机分类器对人脸进行训练和识别。实验表明,该方法提高了人脸的识别率。
关键词: 人脸识别;局部线性嵌入;模糊聚类;支持向量机
0 引言
人脸识别[1-3]是基于人的脸部特征信息进行身份识别的一种技术,它属于生物特征识别技术,是根据生物体(一般特指人)本身的生物特征来区分生物体个体。人脸识别基于人的脸部特征,对输入的人脸图像进行分析、学习,从而完成识别。该技术被广泛用于政府、军队、银行、社会福利保障、电子商务、安全防务等多个领域。
人脸识别是一个复杂的过程,其关键在于特征提取和识别,近年来建立在统计学理论基础上的支持向量机(Support Vector Machine,SVM)[4-7]方法逐渐被认可,由于其具有良好的概括能力,因而被应用于人脸识别。但是,由于人脸数据维数庞大,导致分类算法过于复杂,致使错分点增加,从而影响识别的效果。局部线性嵌入(Locally Linear Embedding,LLE)[8-9]算法是一种基于流形学习的非线性降维算法,可以用来进行特征提取,但是该算法容易受到近邻点选取的影响;参考文献[10]提出了一种改进的局部线性嵌入算法(CLLE)[11-15],在LLE的基础上构造近似重构系数,能够很好地对重构误差加以约束。
因此,本文在参考文献[10]的基础上提出一种基于CLLE和SVM的人脸识别方法,对预处理好的人脸图像利用CLLE进行特征提取,在低维空间中采用SVM进行学习训练和识别样本数据,此方法的识别率相比于已有方法有所提高,从实验中可以得到证实。
1 基于模糊聚类的LLE
对于给定的高维观测数据集X={x1,x2,…,xN},xi∈RD,采样自d维流形,求低维坐Y={y1,y2,…,yN}。设样本点聚类分类的类别个数为C,mj为第j类样本的中心, n(j)为第j类样本的个数。则第j类样本点的内部平均距离为:
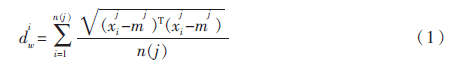
第j类样本与总体样本中心的距离为:

其中,m为总体样本的中心。
由此,定义样本点重构误差的近似重构其中,j为样本点i所属的类,j=1,2,…,C。
算法基本步骤如下[10]:
(1)选取近邻点。对给定的数据集X={x1,x2,…,xN},利用欧式距离找到每个样本点xi的k(k<N)个近邻点。
(2)重建权值矩阵。使数据点的重建误差最小,即求最优化问题:
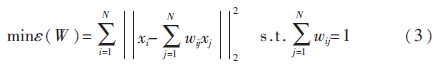
其中,xij(j=1,2,…,k)为xi的k个近邻点,wij是xi与xij之间的权值。
(3)由数据点的局部重建矩阵寻找低维嵌入Y。引入近似重构系数,求解:
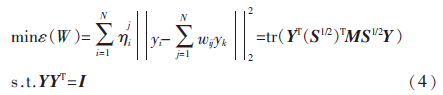
其中,M=(I-W)T(I-W)。
输出(S1/2)TMS1/2的2~(d+1)个非零特征值对应的特征向量。
2 SVM
SVM是以统计学习理论为基础的一种机器学习算法,能够很好地解决小样本、非线性问题。SVM的主要思想是用非线性映射?准将数据映射到高维特征空间中,在高维特征空间中利用最大间隔超平面对线性不可分的数据进行线性划分操作,从而达到分类的效果。
SVM基本流程如下:
(1)将Tr={(x1,y1),(x2,y2),…,(xl,yl)}∈(X,Y)l作为训练集,其中,xi∈X=Rl是每一个训练样本点,yi∈Y∈{-1,1}是训练集中样本点的类别,i=1,2,…,l。
(2)利用恰当的核函数K(xi,xj)和惩罚参数C进行高维映射,求解最优化问题:
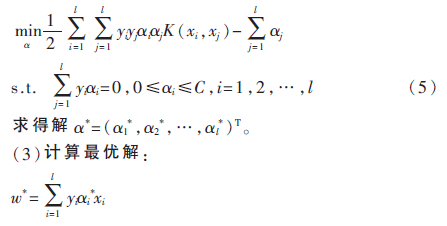

由此判断测试集类别。
3 基于模糊聚类LLE和SVM的人脸识别的基本步骤
本文算法的具体步骤如下:
(1)图像预处理;
(2)读入样本训练集;
(3)利用改进的LLE算法对图像进行降维,提取样本集的特征;
(4)利用SVM对训练集样本进行学习,识别测试集样本。
4 人脸特征提取
4.1 实验准备
实验中用到的人脸图像从ORL人脸数据库中选取。该数据共有40个人,每个人有10幅图像,分别具有不同的表情,共有400张图像。实验选取每个人的前5张图像作为训练集,共有200张图像,共分为40类。剩余的图像作为实验的测试集。部分人脸图像如图1所示。

4.2人脸特征提取
为了能够清楚地对比人脸特征提取方法,从ORL人脸数据库中选取5个人的图像,分为5类,每个人10张图像。每一个点代表一幅人脸图像,降至2维。图2为LLE算法和改进算法CLLE在领域数K=15时的降维效果图。
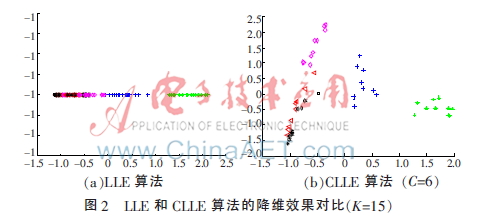
从图2可以看出,CLLE算法将人脸数据降至2维后,不同的人已经可以被明显地区分开来,而LLE算法效果则不明显。

当K=11时, LLE算法和CLLE算法的降维效果对比如图3所示。可以看出,CLLE算法已经可以对人脸数据进行很好的分类,效果十分明显,而LLE算法取得的效果则稍稍比K=15时略好一点。
从实验结果可以看出,LLE算法易受邻域数K的影响,而对于K的不同取值,CLLE算法却可以普遍取得好的效果。
5 人脸识别
5.1 算法参数的选取
5.1.1 核函数的选取
核函数的选取决定了学习分类的好坏。常用核函数主要有线性核函数、多项式核函数、径向基核函数以及Sigmoid核函数。使用这4种核函数对人脸数据进行分类识别,结果如表1所示。易知对于实验的人脸数据,在线性核函数下分类的准确率最高。
5.1.2 邻域个数的选取
在选取聚类个数C时,若选取太大,会影响实验的运行时间,因此实验选取C=6,并利用CLLE算法将人脸数据降至60维,进行训练测试。不同邻域数的分类准确率如表2所示。由表2可知,当聚类个数为6、邻域个数为5时分类识别率略高一些。
5.2 不同分类方法对识别率的影响
表3为4种分类方法在人脸识别上的应用效果。
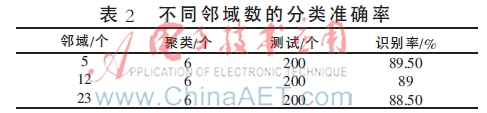
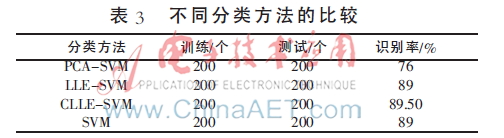
表3表明,CLLE-SVM算法在人脸识别中优于其他三种算法,人脸识别率可达到89.5%。
6 结论
本文利用基于模糊聚类的LLE算法对人脸数据进行降维,在低维空间中利用SVM训练学习已知样本,从而识别人脸类别。实验表明,该方法得到的人脸识别率相对于已有方法有了显著的提高,从而证实了其有效性和可行性。
参考文献
[1] Wang Jing, Su Guangda, Xiong Ying, et al. Sparse representation for face recognition based on constraint sampling and face alignment[J]. 清华大学学报(自然科学英文版), 2013 (1):62-67.
[2] BRUNELLI R, POGGIC T. Face recognition: features ve- rsus templates[J]. IEEE Transactions on PAMI, 1993,10 (15),1042-1052.
[3] CHELLAPPA R, WISLSON C L, SIROHEY S. Human and machine recognition of faces: a survey[C]. Proceedings of the IEEE, 1995,83(5), 705-741.
[4] VAPNIK V N.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000.
[5] 李芳.支持向量机在TE过程故障诊断中的应用[J].安徽工业大学学报(自然科学版),2010,27(2):195-199.
[6] 丁娇,梁栋,阎庆.基于WLLE和SVM的植物叶片图像识别方法[J].安徽大学学报(自然科学版),2013,37(4):61-67.
[7] CHANG K P, TEA J K. Objective rating of seam pucker using neural networks[J]. Textile Research Journal, 1997,67(7):494-502.
[8] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500):2323-2326.
[9] SAUL L K, ROWEIS S T. Think globally, fit locally: unsupervised learning of low dimensional manifolds [J]. Journal of Machine Learning Research, 2003,4(12):119-155.
[10] 吴晓婷,闫德勤.改进的非线性数据降维方法及其应用[J].计算机工程与应用,2011,47(2):156-159.
[11] 李新社,姚俊平.模糊聚类分析及其应用研究[J].网络安全技术与应用,2014(1):69-70.
[12] 王和勇,郑杰,姚正安,等.基于聚类和改进距离的LLE方法在数据降维中的应用[J].计算机研究与发展,2006,43(8):1485-1490.
[13] THEODORIDIS S, KOUTROUMBAS K.模式识别(第3版)[M].李晶娇,王爱侠,张广源,译.北京:电子工业出版社,2006.
[14] 王元珍,王健李,李晨阳.一种改进模糊聚类算法[J].华中科技大学学报,2005,33(2):92-94.
[15] BEZDEK J C. Pattern recognition with fuzzy objective function algorithms [M].New York: Plenum Press, 1981.

