摘  要： 针对同一传感器从不同视角拍摄图像的匹配，提出一种Harris-SIFT算法。首先对图像进行多尺度的预处理，使用动态阈值的Harris算子提取特征点，随后生成128维的SIFT特征向量并对特征向量进行相似度检测，最后建立匹配对应关系，实现特征向量的一一匹配。实验结果表明，该算法可有效适用于复杂场景下景物图像的匹配。

　　关键词： Harris算子；SIFT算子；动态阈值；相似度检测

0 引言

　　图像匹配是将不同时间、不同传感器（成像设备）或不同拍摄条件下获取的两幅图像进行配准的过程，目前已经被广泛地应用于遥感数据分析、计算机视觉、图像处理等领域[1]。全景图像的匹配研究是计算机视觉和图像处理领域的重要组成，是一种较好的在复杂场景中匹配景物的方法，把人工绘制交通规划图和计算工程预算转变为机器劳动，既提高了运算精度还减少了运算时间。

　　通常图像的匹配方法[2]主要有基于图像灰度相关的匹配、基于变换域的匹配、基于特征的图像匹配。目前最常见的匹配方法是基于特征的图像匹配，它首先寻找出适合用于匹配的图像特征，如颜色、纹理、边缘、轮廓、特征点以及几何中心等，然后对找到的特征进行映射配准。HARRIS C等人[3]提出了一种通过检测角点来实现图像匹配的方法，利用了图像的自相关函数抗干扰能力强的特点，实验结果表明其对旋转、平移之后图像的匹配具有较高的精确度。参考文献[4]介绍了一种新的特征计算方法，无需设置特定阈值并减少了因经验值K固定导致重要特征点丢失的问题。LOWE D G首先提出了SIFT，随后对SIFT算法[5]进行完善，该算法具有旋转、平移和尺度不变性，是目前图像拼接领域应用较广泛的一种算法。在SFIT基础上改进的算法有很多，比较著名的有SURF、PCA-SIFT、C-SIFT等。

　　复杂场景下的景物图像匹配要求算法的实时性好，精确度高，本文结合Harris算子和SIFT算子的优点，提出了一种适用于复杂场景下景物图像匹配的Harris-SIFT算法。

1 算法原理

　　1.1 Harris角点检测算子

　　Harris算子采用自相关函数运算检测角点[6]，利用一阶偏导描述亮度变化和微分算子反映像素点在任意方向的灰度变化，能有效区分角点和边缘，有较好的旋转不变性和鲁棒性。

　　经典Harris算子计算特征点的响应函数可以表示为：

　　R=Det（M）-K×Trace2（M）（1）

　　其中，K为经验值，0.04≤K≤0.06；Det（M）和Trace（M）分别为2阶实对称矩阵M的行列式和迹。设fx、fy分别为图像x、y方向的梯度值，λ1和λ2是矩阵M的特征值，则有：

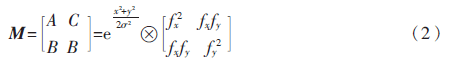
　　设定固定阈值T，当R>T时，可确定R为检测到的特征点。经典Harris算法[7]速度快，稳定性高，且具有良好的旋转不变性和平移不变性，但是Harris不具备尺度不变性，无法适用于复杂场景下景物图像的高精度匹配。结合景物图像实时性高的特征点，算子可以使用动态阈值K，提高实时性。

　　1.2 SIFT匹配算法

　　尺度不变特征转化（Scale Invariant Feature Transform，SIFT）算法提取图像的局部特征进行匹配运算，具有良好的旋转不变性和尺度缩放不变性[8]。

　　SIFT算法是建立在尺度空间理论基础上的。尺度空间就是在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。而尺度空间算子对图像的分析与图像的位置、大小、角度以及仿射变换无关，即满足平移不变性、尺度不变性、欧几里德不变性以及仿射不变性。尺度空间在实现时使用高斯金字塔表示。高斯金字塔的构建分为两部分：（1）对图像做不同尺度的高斯模糊；（2）对图像做降采样（隔点采样）。

　　SIFT算法的金字塔模型是指将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的一层（每层一张图像），每个金字塔共n层。金字塔的层数根据图像的原始大小和塔顶图像的大小共同决定，其计算公式如下：

　　n=log2{min（M，N）}-t，t∈[0，log2{min（M，N）}]（3）

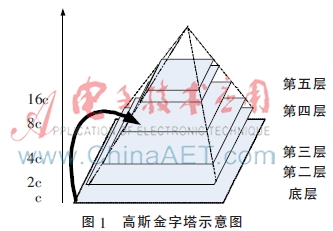
　　其中，M、N为原图像的大小，t为塔顶图像的最小维数的对数值。对于大小为512×512的图像，金字塔上各层图像的大小如图1所示，当塔顶图像为4×4时，n=7；当塔顶图像为2×2时，n=8。

　　但SIFT算法匹配复场景下景物图像时，检测到的特征点太多，特征信息不丰富，且特征点的冗余度高。此外由于每个SIFT特征都是128维的特征向量，而且算法中包含大量的高斯卷积过程，因此运算量十分巨大，匹配的时间较长。SIFT是计算两幅图像之间特征点的相似度来进行匹配的，为进一步提高匹配精度，可以对单幅图像寻找到的全部特征点进行相似度检测，减少算法冗余度，提高匹配精度。

　　SIFT算法的特点有：（1）旋转、尺度缩放、亮度变化保持不变性；（2）特征点数量信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配；（3）多量性，即使少数的几个物体也可以产生大量的SIFT特征向量；（4）可扩展性，可以很方便地与其他形式的特征向量进行联合。

2 Harris-SIFT算法

　　由于景物图像的信息源场景复杂，且特征点相似度较高，本文使用结合了Harris和SIFT优点的Harris-SIFT算法，并在一些具体步骤上使用了新的方法。算法功能如图2所示。

　　（1）预处理

　　在匹配前先对两幅图像进行预处理[9]，采用Retinex算法对图像进行增强处理，预减少灰度、对比度、光照强度对两幅图像的配准精确度的影响。算法共由以下4部分组成。

　　①将输入的图像I（x，y）分离成R（x，y）、G（x，y）、 B（x，y）3幅图像；

　　②确定高斯环境函数，选取3个不同的标准偏差?滓值为：5、80、250，并根据式（4）和式（5）计算出K；

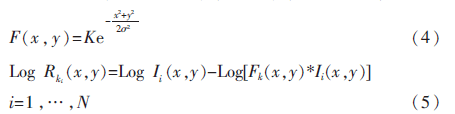
　　③在3个尺度下，分别对R（x，y）、G（x，y）、B（x，y）进行SSR处理，并利用式（6）对结果进行加权处理后得到（x，y）；

　　（2）Harris特征点定位

　　选取Harris算子检测特征点，并针对景物图像实时性较高的特点，采用一种新的Harris特征点计算式（8）。设图像的旋转角度为为任选的两组向量，（x，y）为图像的质心。

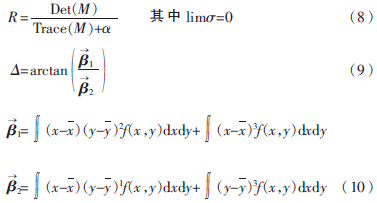
　　（3）生成特征向量

　　随后对Harris算子生成的特征点使用SIFT算法寻找主方向：

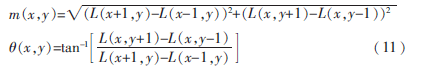
　　其中，L是特征点本身所在空间的尺度函数。对特征点进行采样，并用直方图统计其在尺度空间上的方向特性，随后对统计得到的直方图进行低通滤波处理，选取处理过后的直方图的主方向作为特征点的主方向。

　　确定特征点的主方向之后，需要计算特征向量对特征不变性进行描述。给特征点每个方向的直方图分配8个方向，以关键点为中心取4×4的窗口，然后在每4×4个子区域上计算8个方向的梯度方向直方图，并对4×4个子区域的8个方向的梯度直方图根据位置依次排序，这样就构成了一个4×4×8=128维的特征向量，即为SIFT特征向量。

　　由于复杂场景下建筑图像的特征点信息量相似度较高，为了减少误匹配，对SIFT特征向量进行了相似度检测：

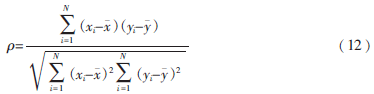
　　分别对两幅图像的特征向量进行斯皮尔曼相关系数的计算，当ρ→1时，表明两个特征点十分相似，舍掉一个，剩余的特征向量用于匹配。

　　（4）建立特征匹配关系

　　特征匹配是对提取到的特征向量间建立起一定的对应关系，利用欧式距离的最小值作为匹配成功的依据。过程由两步实现：①先使用BBF法在两幅图像的所有特征向量中寻找与该特征向量最近邻和次近邻的两个点，并判断该特征向量的最近邻和次近邻距离的比值T是否小于阈值K。若T<K，那么这两点为正确匹配；若T>K，则不是正确匹配。②使用随机采样法来提纯已经匹配好的特征点，剔除错误的匹配。

3 实验结果分析

　　在Core I5处理器，4 GB内存的PC上，使用MATLAB 2010进行仿真，并对实验结果进行比较和分析。

　　图3~图5分别使用三种方法提取特征点，SIFT算子提取到的特征点数量过多，且特征信息不显著的点较多。而Harris算子提取的特征点数量适中，特征点信息丰富，但丢失了一些重要的特征点。表1对比了3种方法提取特征点的性能。经典Harris算子提取特征点数量要小于SIFT，运算时间也较快。而本文算法提取的特征点数量多于经典Harris算子、少于SIFT，此外本文算法检测到的特征点分布比经典Harris均匀，重要特征点的数量也更多；从运算时间分析，本文算法也略快于经典Harris算子。

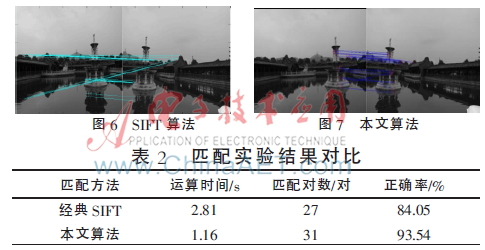
　　图6和图7是分别使用SIFT算法和本文算法对两组图像进行匹配的实验结果。对比两幅图像，本文算法寻找到的匹配处的特征点包含的信息量丰富，匹配分布均匀。而SIFT算子寻找到的匹配处的很多特征点包含的信息量很少且位置相对集中。表2比较了两种算法的性能，本文算法的匹配成功对数多于SIFT算子，匹配正确率较高，运行速度较快，且特征点的数量越多，本文算法的速度优势越大。

4 结论

　　本文结合了Harris角点检测算子和SIFT算法的优点，提出了一种适用于复杂场景下景物图像的Harris-SIFT匹配算法，在一定程度上解决了两个问题：（1）新的Harris特征计算方法，检测到的特征点分布更均匀，缩短了运算时间；（2）通过对SIFT特征向量进行相似度检测，降低了算法冗余度，提高了运算速度和匹配。实验证明了本文算法在复杂场景下对景物匹配的有效性。

　　参考文献

　　[1] 赵启兵，王养柱，胡永浩.基于改进SIFT算法的无人机遥感影像匹配[J].电光与控制，2012（3）：36-39.

　　[2] 陈付平，刘纯平，夏德深.对多尺度边缘检测中边缘位移的研究[J].中国图形图象学报，2003，8（11）：1247-1253.

　　[3] HARRIS C， STEPHENS M． A combined corner and edge detector[C]. Proceedings of the 4th Alley Vision Conference， Manchester： Organizing Committee AVC，1988：147－151．

　　[4] PHILIPPE T， MICHAEL U. Optimization of mutual information for multiresolution image registration[J]. IEEE Transactions on Image Processing， 2000，9（12）：2083-2098.

　　[5] LOWE D G. Distinctive image features from scale—invariant keypoints[J]． International Journal of Computer Vision，2004，60（2）：91-110.

　　[6] 陈浩.基于拉普拉斯金字塔变换的图像融合算法研究[J].激光与红外，2009，39（4）：439-442.

　　[7] 李欢欢.基于HARRIS与SIFT算法的自动图像拼接[J].计算机工程与科学，2012，34（11）：102-106.

　　[8] 吕冀，高洪民.图像制导中的快速算法研究[J].系统工程与电子技术，2009，31（5）：1148-1152.

　　[9] 刘松涛，杨绍清.图像配准技术研究进展[J].电光与控制，2007，14（6）：99-105.