摘 要： 针对常规二维最佳熵法计算复杂，运行时间长，收敛性差等不足，提出基于改进遗传算法的二维最佳熵阈值分割方法。通过对选择、交叉、变异等因子的优化设计，使阈值搜索的鲁棒性与收敛性有了很大改善，并对图像的分割效果进行评价。分析与仿真结果表明，改进算法在大大减少阈值搜索时间的同时，保持了良好的分割性能。
关键词： 二维最佳熵；遗传算法；图像分割；评价指标
0 引言
自20世纪50年代以来，对图像分割方法的研究不断深入与发展，涌现出了许多新理论、新方法。但到目前为止，尚不存在一种通用的图像分割方法。同时缺乏一种评价各种算法性能优劣的判断标准。在众多图像分割方法中，阈值法以其实现简单、计算量小、性能稳定成为图像分割中最基本、应用最广泛的分割技术。但是，如何选取合适阈值以获得理想的分割效果成为阈值分割的一大难点[1]。随着智能算法的不断发展，将智能方法用于阈值的优化成为图像分割研究的热点[2-4]。在繁多的算法中往往存在着诸如算法的抗噪性能、运算时间、全局优化性等方面的不足。此外，各种算法的评价也缺乏完善、客观的标准，如何评判图像分割算法的性能成为图像分割研究的又一大难题。
本文将遗传算法用于图像分割的最优阈值选取中，针对传统遗传算法易陷入局部最优、收敛性速度慢、抗噪能力差等不足提出了改进方法，并通过全局一致性误差函数、概率边缘指数以及变化信息对其性能进行评价分析。
1 基于改进遗传算法的最大熵阈值分割
阈值分割将灰度图像转换为二值图像，不仅极大地压缩了数据，而且大大简化了后续的分析与处理步骤。自Pun根据Shannon熵的概念提出图像熵的定义以来，基于熵的阈值分割方法一直颇受关注。
若一幅图像的灰度空间为G={0，1，2，…，L-1}，其中，灰度值为i的像素个数为ni，则图像的熵定义为：
其中，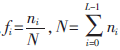
，fi表示灰度值i在图像中出现的频率，N为图像的总的像素数。
传统遗传算法易陷入局部最优，且在噪声背景下收敛速度较慢，甚至出现接近最优的个体被淘汰，进化过程不收敛。为此本文对传统遗传算法的选择、交叉、变异因子进行优化设置，从而增强变异的多样性，加快搜索的收敛性，以获得全局最优解。其基本思路如下：
（1）编码
对于灰度值在0~255之间的图像，一维最佳熵分割可采用8位二进制代码分割值，由于二维最佳熵分割待分割值是二维的，本文采用16位二进制码表示分割阈值，前8位表示分割值s，后8位表示分割值t。
（2）初始化种群
针对二维阈值分割，采用均匀分布在（0，0）~（255，255）之间随机产生的n对个体，编码为16位二进制码。
（3）适应度函数
根据最佳熵阈值分割原理，选择背景和目标的熵测度函数作为适应度函数，即：
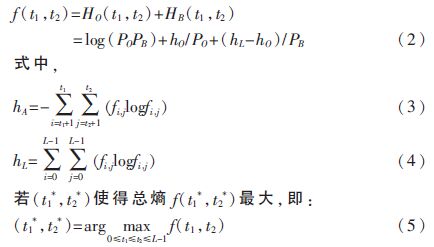
则（t1*，t2*）即为所要求的最佳阈值。
（4）选择
采用赌轮选择和精英策略相结合的方法，首先将种群中各个体的适应度除以种群总的适应度，得到个体的相对适应度。相对适应度大的基因被遗传到下一代，而相对适应度较小的基因则逐步被淘汰。而后利用精英策略将适应度最大的个体以一定比例直接复制到下一代。该方案不仅保证了最优个体绝对复制到下一代，而且还体现了适应度越高的个体繁衍后代的几率越大的进化思想。
（5）交叉
由于二维阈值法的前8位和后8位分别代表不同的阈值，因此采用双点交叉法。若交叉概率选取过高，则个体更新较快，可达到更大的解空间，但对已有的较优模式的破坏性也越大。反之，交叉概率过低，搜索范围的减小，导致最优解的搜索变得迟钝。为了保证交叉后的新个体向着最优解的方向进化，采用如下规则：
若f（t1，t2）（X′）>f（t1，t2）（X）
则X′=（x0，…，xm，ym+1，…，y7，x8，…，xn，yn+1，…，y15）
否则X′=X
若f（t1，t2）（Y′）>f（t1，t2）（Y）
则Y′=（y0，…，ym，xm+1，…，x7，y8，…，yn，xn+1，…，x15）
否则Y′=Y
其中，X=（x0，…，x7，x8，…，x15）与Y=（y0，…，y7，y8，…，y15）为两个交叉的父个体，X′与Y′为新子代个体。交叉点的位置前8位为m，后8位为n，且0<m<7，0<n<7。
（6）变异
本文采用这样一种自适应的变异策略：若当前变异个体的适应度比群体的适应度平均值大，则使其以较小的概率变异，因为它代表着较优的个体，反之则以较大变异概率繁殖下一代，以保持种群的多样性。变异概率bm表示为：
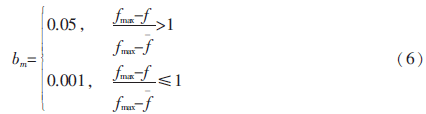
其中，fmax表示当前种群中适应度函数的最大值，f是适应度的平均值，f为当前产生变异个体的适应度值。
（7）算法终止判断
选择当前群体的平均适应度与上一代的平均适应度值之比R0作为算法的终止条件，当算法达到最大迭代次数或者终止条件时停止，输出此时的最佳阈值。
2 分割评价指标
对几种图像分割方法的性能评价，除了采用一些常用的指标（如阈值、迭代次数、时间等）外，还引入全局一致性误差、概率边缘指数、变化信息对分割后的图像进行比较。
2.1 全局一致性误差
全局一致性误差（Global Consistency Error，GCE）是定义在局部细分误差基础上的，局部细分误差定义为：
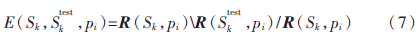
其中，<R>表示集合R中元素的个数，符号“\”表示差集。原始图像中的像元为pi，参考分割结果中pi∈Sk，实际分割结果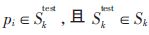
。则全局一致性误差可以用下式表示：
GCE取值范围为[0，1]，其值越小，说明全局一致性误差越小。
2.2 概率边缘指数
概率边缘指数（Probabilistic Rand Index，PRI）是一个检验实际分割结果与参考结果之间的属性共生的一致性的参数。对于任一像元对（xi，xj），设其在原图像S的标记为（li，lj），在分割图像中的标记为（l′i，l′j），PRI的计算公式如式（9）所示，其值越大则分割结果与参考值之间的属性共生一致性也就越好，PRI的取值范围在[0，1]内。
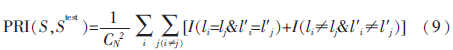
其中，N为总的像元数目，I表示一个判别函数。
2.3 变化信息
变化信息（Variation of Information，VI）是利用参考分割图像的熵、实际分割结果的熵以及参考分割图像与实际分割结果的联合熵这3个参数来衡量实际分割结果相对参考分割图像的信息变化。变化信息越小，说明实际分割结果相对参考分割图像信息变化越少，实际分割结果越接近参考分割图像。
3 实验结果与分析
选择一幅255×255的米粒灰度图像作为仿真对象。选择种群规模为20，最大迭代次数为200，精英策略将适应度最大个体以10%直接复制到下一代，终止条件R0取[1.0，1.000 5]，交叉率取0.7。分别采用一维最大熵法、二维最大熵法与本文方法在不同的条件下进行仿真比较分析。
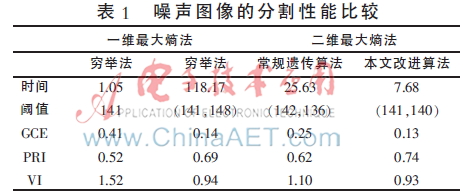
图1为未经处理的原始图像，对噪声图像的分割效果如图2所示，表1为对应的分割性能指标。可以看出，一维最佳熵法对低信噪比图像的分割效果明显下降。而二维最佳熵法能够有效降低干扰的影响，但噪声的影响使得穷举法与传统遗传算法的搜索时间变得更长。从全局一致性误差、概率边缘指数以及变化信息中可以看出，改进的遗传算法在大大减少搜索时间的同时，保持了良好的分割效果。
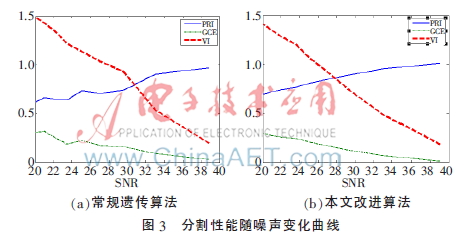
为了进一步分析噪声对各种算法的影响，仿真分析不同信噪比下性能指标的变化情况，如图3所示。可以看出，随着噪声强度的增加，图像分割性能指标不断恶化；相同SNR下，改进算法的性能要优于常规遗传算法。
4 结论
本文首先介绍一维、二维最佳阈值分割方法的原理；而后针对二维最佳熵法的阈值搜索空间大、算法的运行时间长、收敛性差等不足，提出了基于改进遗传算法的最佳熵阈值分割算法。通过对选择、交叉、变异等因子的优化设计，使新算法的收敛性以及分割效果有了明显改进。最后通过图像分割评价指标验证了改进算法在噪声图像分割中的高效性。
参考文献
[1] OTSU N. A threshold selection method from gray level histograms[J]. IEEE Transactions on Systems， Man and Cybernetics， 1979， SMC-9（1）：62-66.
[2] 汤可宗，柳炳祥，徐洪焱，等.一种基于遗传算法的最小交叉熵阈值选择方法[J].控制与决策，2013，28（12）：1805-1810.
[3] CHANDER A， CHATTERJEE A， SIARRY P. A new social and momentum component adaptive PSO algorithm for image segmentation[J]. Expert Systems with Applications， 2011，38（5）：4998-5004.
[4] 汤官宝.基于量子粒子群的改进模糊聚类图像分割算法[J].微型机与应用，2014，33（15）：40-42.