摘 要: 稀疏优化后的同心圆阵的旁瓣电平虽然相比于满阵有所降低,但还是很高。为了获得具有更低旁瓣电平的同心圆阵,本文采用锥型波束形成技术,对利用模拟退火粒子群算法得到的稀疏同心圆阵加窗,优化阵列馈电电流的激励振幅。利用改进的三角窗、汉宁窗和布莱克曼窗三种窗函数对稀疏同心圆阵进行优化。仿真结果表明,加窗后,稀疏同心圆阵的旁瓣电平都有明显降低,采用布莱克曼窗得到的阵列的最大旁瓣电平最小,汉宁窗的次之,三角窗的最大。
关键词: 稀疏同心圆阵;窗函数;旁瓣电平
0 引言
同心圆阵天线[1-2]具有结构简单、扫描范围宽、波束方位控制灵活等特点,被广泛应用于雷达、声呐、移动通信和电子系统中。但同时存在阵列阵元数目较多、系统成本大、旁瓣电平高等缺点。稀疏阵列天线[3-6]能有效解决以上问题。然而稀疏后的阵列天线的旁瓣电平往往较高,为了进一步降低同心圆阵的旁瓣电平,采用锥型波束形成技术,对阵列馈电电流的激励振幅进行优化,使阵列中心圆环的阵元激励振幅最大,最外环的阵元激励振幅最小。
一种锥型波束形成的方法是在滤波器中进行波束形成,通过窗函数改善阻带特征[7]。但要对信号滤波中的窗函数进行改进,使之适用于具有同心圆结构的阵列天线。本文分别将改进的三角窗、汉宁窗和布莱克曼窗应用到稀疏同心圆阵中,比较其阵列方向图,分析其性能。
1 同心圆阵
同心圆阵是由多个具有共同圆心的均匀圆阵组成的平面阵,如图1。
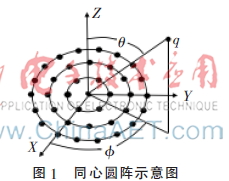
对于阵列天线,如果阵元间距超过信号半波长,阵列方向图会出现高的栅瓣。然而如果阵元间距小于半波长,阵列方向图会有较宽的主瓣宽度,而且阵元间的互耦效应会增大。因此,设计同心圆阵列天线时,每个圆环上的阵元间距设置为半波长。
设均匀同心圆阵由M个圆环构成,每个圆环之间间隔dc=λ/2,每个圆环的半径rm=mλ/2。位于同一圆环上的阵元等间隔均匀分布,每个圆环上的阵元间距dm≈λ/2,则第m个圆环上的阵元个数:
Nm=2πrm/dm=2πm(1)
阵元的个数应该是整数,由式(1)得到的结果要向下取整。
把圆心位置的阵元作为阵列的参考阵元,阵元为理想的全向性天线单元,各阵元等幅同向激励,阵列主波束指向阵列中心法线方向,同心圆阵方向图函数为:
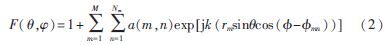
其中,![WB]05SG11}OXJC`__HAL4CA.jpg WB]05SG11}OXJC`__HAL4CA.jpg](http://files.chinaaet.com/images/2016/02/23/6359184739312100009957115.jpg) 为第m个圆环上第n个阵元对应的方位角,
为第m个圆环上第n个阵元对应的方位角,![WB]05SG11}OXJC`__HAL4CA.jpg WB]05SG11}OXJC`__HAL4CA.jpg](http://files.chinaaet.com/images/2016/02/23/6359184739933000002904269.jpg) =2π(n-1)/Nm;k=2π/λ,λ为信号波长;a(m,n)为第m个圆环上第n个阵元对应的阵元激励。
=2π(n-1)/Nm;k=2π/λ,λ为信号波长;a(m,n)为第m个圆环上第n个阵元对应的阵元激励。
2 稀疏同心圆阵
为保证阵列稀疏优化时仍满足阵列孔径约束条件,同心圆阵圆心位置的阵元需保留,不能被稀疏掉。A为阵列中各个阵元位置的幅度加权系数a(m,n)构成的矩阵,以a(m,n)表示该栅格处是否放置阵元。当amn=1时,代表该位置有阵元;当amn=0时,代表该位置无阵元。采用粒子群算法稀疏优化同心圆阵,系数矩阵A映射为一个粒子,粒子中的一个变量对应于一个阵元。以降低同心圆阵天线的旁瓣电平为优化目标,利用其最大旁瓣电平构造目标函数,即:

其中,Fmax为主瓣电平,Fsll max为最大旁瓣电平。目标函数值越小,则旁瓣电平越小,阵列天线性能越好。
粒子的目标函数值决定粒子的位置是否最优。在每次迭代中,粒子根据以往经验寻找最优粒子位置,并通过跟踪两个“最优”粒子的位置来不断更新:一个是单个粒子迄今找到的最优解位置,即个体最优位置;另一个是整个群体迄今找到的最优解位置,即全局最优位置。
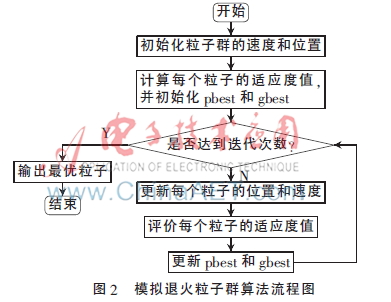
利用粒子群算法对同心圆阵进行稀疏优化的算法流程如图2所示,其中pbsed是个体最优,gbest是全局最优。
3 对稀疏同心圆阵加窗
前文对同心圆阵进行稀疏时,阵列中各单元为等幅激励。为了获得旁瓣电平更低的同心圆阵,对阵元激励进行优化,使阵元激励具有锥型幅度分布,对稀疏同心圆阵加窗。窗函数即为截断函数,采用不同的截断函数对阵元激励的振幅进行截断,以此减小阵列天线的旁瓣电平。
加窗时,阵列的同一圆环上的振幅权重相同,最中心阵元激励的振幅权重最大,由里到外圆环阵元激励的振幅随窗函数变化,最外圆环的振幅权重最小。
3.1 三角窗
对同心圆阵加三角窗,同心圆阵每个圆环的阵元激励振幅权重随三角函数变化,其变化公式如下:
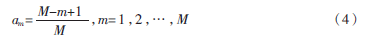
其中,m是指同心圆阵的第m个圆环,M为同心圆阵的圆环个数。同心圆阵的最里圆环的阵元激励振幅权重为am=1,最外圆环的阵元激励振幅权重为am=1/m。
3.2 汉宁窗
汉宁窗是升余弦窗。对同心圆阵加汉宁窗,同心圆阵每个圆环的阵元激励振幅权重随汉宁窗函数变化,其变化公式如下:
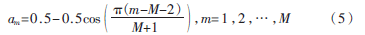
3.3 布莱克曼窗
布莱克曼窗为二阶升余弦窗。对同心圆阵加布莱克曼窗,同心圆阵每个圆环的阵元激励振幅权重随布莱克曼窗函数变化,其变化公式如下:
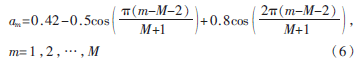
4 仿真结果
设一均匀同心9圆环阵列由223个阵元组成,阵列圆心的阵元作为第一个圆环,计算可得其最大旁瓣电平为-17.37 dB。采用模拟退火粒子群算法对同心圆阵进行稀疏优化,得到的稀疏阵单元数为163,最大旁瓣电平为-21.72 dB,当方位角为0时,其第一零点波束宽度为17.91°。图3为稀疏后同心圆阵阵元分布,以实心圆点代表同心圆阵阵元。稀疏优化后的同心圆阵的方向图如图4所示。
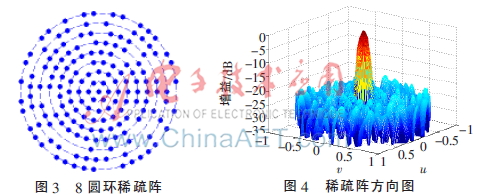
对稀疏后的同心圆阵分别加三角窗、汉宁窗和布莱克曼窗。同心圆阵圆心阵元的激励幅度为1,圆心外8个圆环阵元激励幅度由里到外随窗函数依次减小,得到的阵元激励幅度变化趋势如图5所示。
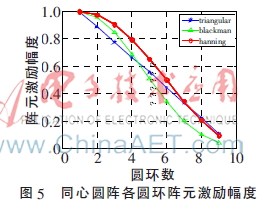
对稀疏同心圆阵分别加三角窗、汉宁窗和布莱克曼窗后,得到的稀疏阵列的最大旁瓣电平分别为-24.23 dB、-24.36 dB和-25.16 dB,其二维方向图分别如图6~8所示,三条曲线分别是方位角为0、π/4和π/2时的方向图。当方位角为0时,得到阵列的第一零点波束宽度分别为31.75°、32.24°和37.61°。
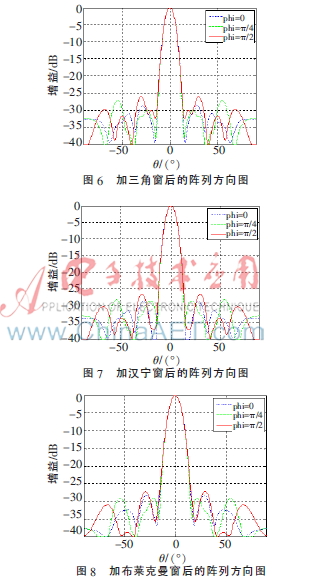
由图6~8可以得出,加窗后稀疏阵列的最大旁瓣电平较加窗前时都有所降低,说明对稀疏同心圆阵加窗可以降低阵列的旁瓣电平。加不同的窗,旁瓣电平降低的程度有所不同。加布莱克曼窗得到的阵列的最大旁瓣电平最小,加汉宁窗的次之,加三角窗的最大,比未加窗的稀疏阵列的最大旁瓣电平分别降低了3.44 dB、2.64 dB和2.51 dB。但阵列旁瓣电平降低的同时,其第一零点波束宽度变宽了,加三角窗、汉宁窗和布莱克曼窗得到的稀疏阵比未加窗的稀疏阵的第一零点波束宽度分别展宽了13.84°、14.33°和19.70°。
5 结论
本文利用窗函数对稀疏同心圆阵的阵元激励振幅进行优化,并分析了加窗后阵列的最大旁瓣电平和第一零点波束宽度的变化情况。通过对三种窗函数下的阵列旁瓣电平进行比较,得出布莱克曼窗的优化效果最好,汉宁窗次之,三角窗最差。从第一零点波束宽度的变化情况来看,随着旁瓣电平的降低,主瓣宽度变宽了。利用加窗的方法降低阵列旁瓣电平是以增大第一零点波束宽度为代价的。
参考文献
[1] CNANG B K, MA X Y, SEQUEIRA H B. Minimax-maxmini algorithm: a new approach to optimization of the thinned antenna array[C]. Antennas and Propagation Society Internatiol Symposium, Seattle, WA: IEEE Press,1994:514-517.
[2] 薛正辉,李伟明,任伍.阵列天线分析与综合[M].北京:北京航空航天大学出版社,2011.
[3] HAUPT R L. Optimized element spacing for low sidelobe concentric ring arrays[J]. IEEE Transactions on Antennas and Propagation, 2008,56(1):266-268.
[4] HAUPT R L. Thinned arrays using genetic algorithms[J]. IEEE Transactions on Antennas and Propagation, 1994, 42(7):993-999.
[5] MANDAL D, SADHU D, GHOSHAL S P. Thinned concentric circular array antennas synthesis using improved particle swarm optimization[J]. Aceee International Journal on Communication, 2011,2(2):21-25.
[6] SINGH U, SINGH D, KAUR C. Thinning of planar circular array antennas using Firfly algorithm[C]. Engineering and Computational Sciences(RAECS), 2014 Recent Advances in. IEEE, 2014:1-5.
[7] DESSOUKY M I, SHARSHAR H A, ALBAGORY Y A. Optimum normalized-gaussian tapering window for side lobe reduction in uniform concentric circular arrays[J]. Progress in Electromagnetics Research, 2007,69(1):35-46.

