杨凯，秦祖军，袁明

　　（桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004）

      摘要：为提高相位光时域反射仪对扰动判断的准确性，研究了两种常用于对其后向散射信号处理的方法。实验结果表明，单一的叠加平均方法在一定程度上能抑制噪声，但耗费时间长，不利于系统的实时性，并且对扰动信息的提取不明显。小波阈值滤波的方法能比较有效地降噪并识别出扰动信息，但需要找到合适的小波基及其分解层次。在实际应用中通过采用多种小波基共同作用的综合判断法，可以减少系统的误判、漏判，提高系统的准确性。

　　关键词：相位光时域反射；降噪；叠加平均；小波基

0引言

　　光纤传感技术是20世纪70年代伴随着光纤技术和光纤通信技术的发展而兴起的一种新型传感技术。它以光波为传感信号，以光纤为传输介质，感知和探测外界被测信号［1］。其中分布式光纤传感技术利用光纤的敏感性，集信息传输和传感于一身，只需一个光源和一根探测线路，可对沿光纤传输路径的传感对象进行检测［2］，实现大范围和长距离的传感测量。

　　相位光时域反射仪是一种基于散射型的分布式光纤传感器，能对光纤沿线上的扰动进行识别和定位，但传感系统得到的后向散射光的信号很微弱，环境噪声的影响使得对扰动点的识别很困难，特别是传感光纤的尾部，信号光的衰减已经很大，其散射光强度几乎淹没在噪声中。并且相位光时域反射仪的相干性原理使得其对环境中微小的扰动极为敏感，容易引入噪声［35］。为提高性能，必须通过信号处理的方法降低噪声，提高信噪比。

1常见信号处理方法

　　1.1叠加平均法

　　叠加平均法理论相对简单，其原理是将某一时刻采集到的M个点的数据（通常是一个或多个周期内的点）存储到某一单元中，如此采集N次均存入该单元，然后对其求N次平均［68］。被采集的信号通常混有噪声并且通常为白噪声，经过N次叠加平均，其信噪比会得到改善。

　　其中，En为N次信号的总噪声，eni为经平均之后的信号噪声。可以看出经叠加平均后，性噪比可以提高N倍，但随着叠加次数的增多，系统消耗的时间也越长。

　　1.2小波变换及小波阈值滤波法

　　小波变换是以某一被称为基本小波(mother wavelet)的函数作位移b后，再在不同尺度a下，与待分析信号x(t)作内积，即:

　　其中，WTx(a,b)为x(t)经小波变换后的结果，是关于a、b的二元函数，随基本小波ψ(t)的不同而改变。b反映位移，a为尺度因子，其作用是对基本小波ψ(t)作伸缩变换；通常ψ(t)在时域上长度很短，两头衰减快，随a值的不同而变化。小波变换在频域上相当于对信号x(t)进行带通滤波，通过a的变化实现带通滤波器中心频率位置和宽度的改变。小波变换具有自适应分析特征，对于信号中低频成分，需要时间分辨率低、频率分辨率高，a会自动变小；而对于高频信号，则a会自动变大，再随着b的改变，信号就能被逐渐分析［9］。

　　通过小波变换的方法对信号进行处理在工程应用中较广泛，其中小波阈值滤波法简洁高效，在许多场合得到应用，其对于相位光时域反射信号的处理也具有一定的适用性。

　　小波阈值滤波是将含有噪声的原始信号经小波分解到不同的尺度中，然后进行阈值处理删除各尺度中噪声的小波系数，最后通过小波重构，得到去噪后的信号。其流程图如图1所示。

　　小波阈值法在去噪过程中，小波基、分解层数、阈值的选择规则、阈值函数的设计都是影响去噪效果的因素。由于不同的小波基函数在处理信号时各有特点，且没有任何一种小波基函数可以对所有类型信号都取得最优的去噪效果，实际应用中往往是通过实验结果来选取最合适的小波基。下文将重点介绍不同小波基及其分解层次对信号处理结果的影响，为使处理后的信号平滑、去噪更有效，选用常用的软阈值函数和固定阈值估计法。

2实验方案设计

　　相位光时域反射系统以26 km长的光纤作为传感光纤，并以0.001 s为周期向光纤中注入光脉冲，在25 km处进行扰动。利用此条件为背景对叠加平均法和小波阈值法进行验证，以测试各个方法的降噪效果以及对扰动信号识别能力。

　　信号处理方案如图2所示，将采集到的后向散射实时信号与已存储的无扰动时的信号相减得到后向散射差值信号，进而分别进行上述方案的测试。（1）单独叠加平均法：采集每个周期内的差值信号进行不同次数的叠加，之后进行平均处理。（2）小波阈值法：通过选定的小波基对差值信号进行多层次分解与重构。

3实验结果及分析

　　根据上述方案对信号进行处理。图3所示为经过200次、500次叠加平均之后的信号。由系统中光脉冲周期为0.001 s可知，完成上述累加系统所需时间分别为0.2 s、0.5 s。

　　从图3可以看出，叠加次数越多信号的噪声会越小，但也注意到扰动点的信息也会越来越模糊，这不利于系统对扰动信息的识别，而且随着叠加次数增多系统消耗的时间会越长，大大影响系统的实时性。

　　小波阈值法选用haar小波、db5小波、sym8小波和coif1小波作为母小波，分别对信号进行二、三、四层次的分解与重构，比较分析其各自结果。

　　图4所示为基于haar小波的小波阈值信号处理图。harr小波是最简单的小波，本质上是阶跃函数，主要特点是计算简单。从图4可以看出，经过处理后的信号信噪比得到较大改善，随着分解重构层次的增多改善程度越大，信号失真度也越大。对于扰动信息的提取，haar小波的分解重构表现出很好的性能，图中所示两层、三层、四层的分解重构信号都能较为明显地得到扰动信息，但随着分解层次的增多扰动信息的识别度会有所下降。

　　图5所示为基于db5小波的小波阈值信号处理图。dbN（N表示阶数）是Daubechies小波的表示。对于相位光时域反射信号，N取值为5时效果较好。从图中可以看出，经db5小波处理后的信号降噪效果良好，两层、三层分解重构后的信号对扰动信息的识别明显。图5基于db5小波基的小波阈值信号处理图

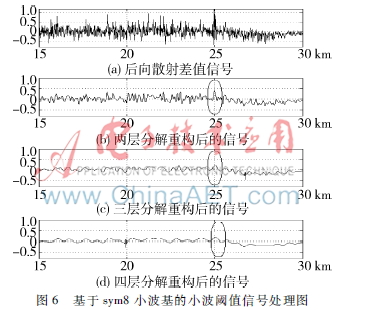
　　图6所示为基于sym8小波基的小波阈值信号处理图。symlets小波的构造类似db小波，但symlets小波具有更好的对称性，能减少重构时的相移。其中sym8小波对相位光时域反射信号分析具有较好的效果。从图6可看出经sym8小波的两层分解重构后的信号能较好地分辨出扰动信息，而经其三层、四层分解重构后的信号虽然信噪比得到改善但对扰动信息的识别不明显。

　　图7所示为基于coif1小波基的小波阈值信号处理图，coiflet小波在信号处理、数值分析、故障诊断等方面应用广泛，其中coif1小波适合对相位光时域反射信号的处理。从图7可以看出，信号经过coif1小波分解重构后都能有效地提取出扰动信息，信号的降噪也较为明显。

　　从图4~图7可以看出，对于信噪比较高的后向散射信号通过上述4种不同的小波基分解重构后，基本上都能分辨并提取出扰动信息。其中haar小波和coif1小波的处理结果表现得比另外两种小波好。但它们都会出现随着分解重构层次变大，提取到的扰动信息变得很微弱、信号的信噪比有所下降的情况。这是因为分解层数越大，噪声和信号表现的不同特性越明显，越有利于二者的分离。但另一方面，分解尺度越大，重构得到的信号失真也会越大，在一定程度上又会影响最终去噪的效果。

　　在许多应用场景中由于外界环境恶劣，得到的后向散射差值信号信噪比较低，仅单独采用某一种小波的分解重构对信号进行分析，往往会使最终的结果出现偏差，导致系统的准确性降低。图8所示为实验中模拟得到的信噪比较低的后向散射差值信号，从图中已经很难辨认出在25 km处的扰动信息。

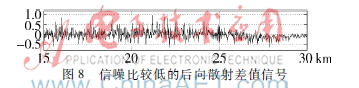
　　图9经小波阈值处理后的信号图9是经过上述4种小波第三层分解重构后的信号图。从图可以看出经sym8小波分解重构后的信号在扰动位置突出不明显，其对扰动信息的识别已很困难。经db5、coif1小波分解重构后的信号，在扰动位置信号有突出，但噪声幅值和扰动位置信号幅值相差不大，并不能区分出噪声和扰动信息。而经haar小波分解重构后的信号不仅信噪比得到改善，而且能较明显地提取出扰动信息。由此可知仅通过一种或两种小波基的小波阈值方法对信号分析会使系统准确性下降，而基于多种小波分析的综合判断法能在一定程度上减少系统的漏判、误判，提高系统的准确性。

4结论

　　相位光时域反射仪中后向散射信号的处理结果直接关乎系统性能，为此本文重点论述了常用于对其后向散射信号进行处理的叠加平均滤波法和小波阈值滤波法，并进行了相关实验。叠加平均法能有效改善信噪比，并且随叠加次数的增多改善效果越明显，但这会降低系统的实时性，而且通过实验发现叠加平均法对扰动信息的提取并不明显。小波阈值滤波法的实验中分析了haar、db5、sym8、coif1 4种不同的小波基及其分解层次对信号处理结果的影响。在后向散射差值信号信噪比较高时，经上述4种小波基分解重构后的信号降噪明显，基本都能识别出扰动信息，并且经haar、db5小波基处理结果优于另外两种。在后向散射差值信号信噪比较低时，4种不同的小波基分解重构后的信号存在较大差异，仅通过某一种小波基处理的结果来判断扰动信息存在一定的局限性，系统的误判、漏判增多，但通过这4种小波分解重构结果的综合判断能比较有效地提高系统对扰动信息提取的准确性。

参考文献

　　［1］ 张旭苹.全分布式光纤传感技术［M］.北京：科学出版社，2012.

　　［2］ 李川.光纤传感技术［M］.北京：科学出版社，2012.

　　［3］ 王杰.超长距离相敏光时域反射仪实验与应用研究［D］.成都：电子科技大学，2013.

　　［4］ 吴麻伟.基于相敏光时域反射技术的分布式光纤围栏入侵监测应用研究［D］.成都：电子科技大学，2012.

　　［5］ 丁伟伟,赵霞.GSMR光纤分布式系统的时延测量与自动补偿［J］.微型机与应用,2015,34(20):7275,79.

　　［6］ 李星蓉，李永倩，张硕.同步叠加平均算法抑制噪声的Labview实现［J］.华北电力大学学报，2009，36（4）：7376.

　　［7］ 吕媛,秦祖军,梁国令，等.融合数字累加平均和小波变换的信号降噪测试［J］.微型机与应用,2015,34(7):1315,19.

　　［8］ 周倩婷，危峻，徐志鹏.噪声特性对多次采集累加平均技术的影响［J］.红外与激光工程，2010,39(5):959962.

　　［9］ 张晓佳,毛永毅,张晨晨，等.基于小波变换的场强定位算法［J］.微型机与应用，2015，34（12）：6163.