陈鹏,杨立
(浙江工业大学 信息工程学院,浙江 杭州 310023)
摘要:就目前桥梁监测系统可视化的现状,从数据插值和VRML两个方面总结了现有研究工作,针对目前桥梁健康监测需求提出了一种基于Kriging插值和VRML的桥梁监测系统数据可视化方法。首先使用修改过的Kriging算法对由桥梁健康监测传感器网络得到的数据进行插值,并为数据点赋予相应颜色,最后将结果加载到三维模型中。实验结果表明,该方法简单快捷,实现了较高的插值精度和可视化效果,在桥梁健康监测数据可视化实现方面具有广泛用途。
关键词:桥梁健康监测;数据插值;VRML;可视化
0引言
目前,桥梁结构监测的布点主要集中在桥梁受力、承重的关键点。而桥梁是一个无限自由度的整体,单从有限的传感器布点是无法得到完整的桥梁健康状况信息的,因此需要一种可靠的方法插值出未布置传感器的桥梁位置的各参数数值;现有的桥梁监测系统大部分都是以报表及二维曲线图等作为主要的展示形式,这种方法不形象直观,已不能满足当前监测工作的需要;而三维显示技术可以生动形象地再现现实世界中的实物,这种技术即是可视化技术。插值,也叫做内插,意思是在离散数据基础之上插补连续函数,使得这条插补之后的连续曲线可以通过全部既定的离散的数据点。本文采用了目前较为先进的Kriging插值方法用以获得未布置传感器点处的监测值。
VRML(Virtual Reality Modeling Language)是虚拟现实建模语言。参考文献[1]研究了如何利用VRML来建立虚拟城市。参考文献[2]研究了基于VRML的虚拟校园的设计与实现,并以实验结果证明了VRML技术仍具有广阔的应用前景。VRML作为一门独立的三维建模语言,命令简单上手快,且与txt同为ASCII编码,可以直接使用文本编辑器编辑。
1建模及插值
1.1建立桥梁三维模型
整个桥梁系统可视化过程中,首先要做的是建立桥梁的模型,本文采用SolidWorks建立这一桥梁模型。首先在SolidWorks中逐个建立桥梁的各个部件,例如桥面、索塔等,各个部件建立完成后按照实桥结构进行组装,得到完整的三维桥梁模型,如图1所示。

1.2监测数据插值
桥梁结构监测传感器主要集中部署在桥梁受力、承重的关键点。目前应用较为广泛的插值算法主要有克里格插值算法、泰森多边形插值算法以及反距离权重插值算法[4]等。
反距离权重法缺少对各向异性的考虑,估算精度很成问题;泰森多边形法构造多边形容易产生奇异多边形,估值准确度不高;克里格法考虑了空间属性的各向异性和已知点的“从聚效应”,实现了对待求点无偏、线性以及最小估计方差的估算,插值精度高。文中采用针对桥梁数据特征修改过的克里格法进行桥梁健康监测数据插值。
应用克里格法的桥梁数据插值步骤如下:
(1)当空间点x在一维x轴上变化时,一维条件下x轴方向上的区域化变量Z(x)的变异函数定义为桥梁监测数据Z(x)在空间坐标点x和x+h处得到的监测值Z(x)与Z(x+h)之差的方差的1/2,记为γ(x,h),即:
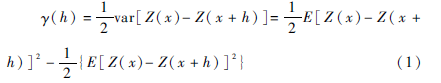
在二阶平稳假设条件下,有:
h,E[Z(x+h)]=E[Z(x)](2)
因此:
γ(x,h)=12E[Z(x)-Z(x+h)]2(3)
变异函数依赖于两个自变量x和h,在对主桥面应力应变传感器布点分析上,根据桥梁力学结构特点变异函数γ(x,h)只与传感器之间的相对距离h相关,γ(x,h)即为γ(h):
γ(h)=12E[Z(x)-Z(x+h)]2(4)
理论变异函数模型采用球状模型,球状模型的公式为:

其中,c0为块金常数,c为拱高,c0+c为基台值,a为变程。
(2)参估点的搜索。结合桥梁实际监测布点,四方搜索方案是根据插值点的横坐标和纵坐标把平面分成4个象限,以变程a的长度为搜索半径,在每一个象限中查找与插值点距离最近的已知样本点;
(3)结合桥梁实际监测布点的变异函数,采用Kriging法进行应力应变监测数据的空间插值分析:

其中,λi是待定权重系数。
权重系数的求取满足两个条件:
①使Z*(x)的估计是无偏的,即偏差的数学期望为零。正常情况下,监测数据是平稳的,即:
E(Z*(x))=m(7)
其中,m为一常数。
当:
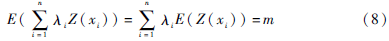
则有:

其中,xi为第i个已知点的监测值,λi为权系数。
②使估计值Z*(x)与实际值Z(x)之差的平方和最小,即:

其中,x0为待估点,αi、αj分别为xi、xj的系数。
根据拉格朗日乘数原理,令:

其中,λi和μ分别为权系数和拉格朗日乘数。
求F对λi和μ的偏导数,并令其为0,得Kriging方程组:

即:
Kλ=D,λ=K-1D(13)
其中,K为协方差矩阵,cij表示第i和第j个已知点的协方差,λ为权系数矩阵。根据式(13)即求出权重系数λi和拉格朗日乘数μ,从而求得未知点的估计值。
以杭州某大桥2014年12月1日02:00:00采集的应力数据为样本插值得到的图如图2所示,其中整个桥面网格化分成了80×880个节点,图中黑点为传感器所在位置。

2颜色映射
因为颜色映射时大部分为矩阵运算,故采用MATLAB进行运算得到前述point、coorIndex以及color三组数据。计算color矩阵时采用的方案是列一组色表,如图3所示。数值从小到大,颜色从深蓝到橙红,超过阈值的直接赋为红色以示报警。此色表共有49个间隔。此时有两种方法可为数据点赋予颜色:(1)值域均匀分布:按照传感器数值0~阈值将其不均匀(按监测数据分布范围非线性划分)地分成49个间隔(数值较小段间隔较大,反之亦然),网格节点的数值落在哪个区间即赋予其相应的颜色,效果如图4所示;(2)数据点均匀分布:此方法把除了超出阈值外的数据点均匀分布在了49个色彩区间内,每种颜色都有同样数目的数据点。具体步骤为先把整个n×11n的数值矩阵转换成一维数组,再对这个数组进行升序排序,使用二分查找法找出这个一维数组中超出阈值的最小元素值,将此元素之后的全部元素(数量m)对应的颜色都设为红色,表示此数据点是超出阈值的。(n×11n-m)/图6桥梁数据可视化效果图
49=k,即每个颜色对应的数据点有k个,将排序后去掉超出阈值元素的一维数组按k间隔分成49段,即得到对应的颜色矩阵。最终效果如图5所示。肉眼可以直接看到,数据点均匀分布法效果更为明亮,且每种颜色都有数目相同的数据点,显示效果更好,因而在此采用数据点均匀分布法为数据点赋予颜色。

3结果导入
在使用MATLAB得到可视化的主要数据之后需要将结果添加到图中相应位置。MATLAB程序本身不适合此项工作,本文选择使用C#编程来处理。将此MATLAB程序打包为.dll文件,添加到C#程序的引用中。需要注意的是在MATLAB中进行dll打包时的类名即是在C#程序中引用时所需要的类名。
最终桥面应力变化可视化效果如图6所示。

因为桥梁监测数据是连续变化的,所以可视化之后得到的效果图也会如前述的色表从某一较高点均匀往外围过渡,桥面上红点即是监测数据超出了传感器报警阈值所赋予的红色。在桥梁监测系统中引入此可视化部分可以让监测者一目了然地看到桥梁较为危险的区域,从而及早预防,有效防止桥梁事故的发生,保障交通运输的安全。4结论
本文提出了一种基于Kriging插值、VRML桥梁监测系统数据可视化方法。该方法简单,易于操作与实现,对设备计算处理要求低,且不需要依赖大型三维建模辅助软件,因此具有较好的应用前景。
参考文献
[1] 李冉,蔡正林.结合VRML和Java建立动态场景[J]. 电脑与信息技术,2005,13(1):3335,66.
[2] 李欣.基于VRML的虚拟校园设计与实现[D].长沙:国防科技大学,2005.
[3] 张雄辉,郑力新,周凯汀,等.基于区域划分的快速图像插值算法[J].微型机与应用,2013,32(14):3840.
[4] 赵坡. 地质体三维建模空间插值与可视化算法研究及实现[D]. 成都:成都理工大学, 2013.
[5] 朱延博,王竹林,张自宾,等.基于图像插值的电视测角仪视场变换系统设计[J].电子技术应用,2014,40(2):8587,90.

