龚健

　　(广州铁路职业技术学院，广东 广州 510430)

　　摘要：传统无线传感网络定位算法没有考虑节点移动问题，采用多次测量、推算节点运动轨迹方式估算节点位置，定位偏差偏大。针对节点移动会对周围信号产生波动和多普勒频移，提出一种基于移动节点信号衰减渐变模型，利用极大似然估计算法思想将移动节点对周围RSSI指纹参量影响转变为概率事件，并通过泰勒级数修正渐变模型。仿真实验证明，新算法既可以减少对移动节点定位偏差，又可以有效弥补RSSI易受环境干扰的不足。

　　关键词：极大似然估计算法；泰勒级数；接收信号强度指示；衰减渐变模型

0引言

　　在无线传感网络中，路径传播损耗定位算法属于测距算法，首先根据信号强度与传播距离损耗规律建立衰减模型，再依据实测节点信号强度测算之间距离，通过多边测量、圆周或双曲线函数计算节点位置［12］。RSSI接收信号强度指示算法属于非测距算法，节点通过采集的信号参数与指纹数据库进行最近匹配，从而估算节点位置。然而这两类算法都没有考虑到节点移动问题［3］。在实际工程中，锚节点位置通常会随环境变化而移动，如对大气、洋流的监测，如何利用现有设施实现对移动节点的精确定位是目前无线传感网络研究的难点和热点。

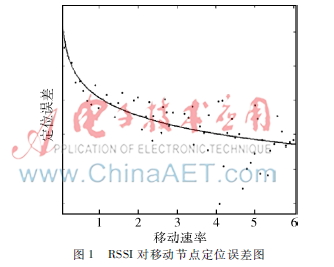
　　目前业界对移动节点定位研究尚不成熟［45］。为避免算法过于复杂，一般采用多次测量，推算运动轨迹方法，以时间换取空间计算的复杂度。由于每次节点定位都存在误差，很难描述节点真实运动状态［6］，因此多次测量方法定位偏差较大，难以满足真实工程需求。RSSI算法对静止节点定位精确，但易受信号波动和多径衰减影响，同时锚节点移动会对周围信号产生信号波动和多普勒频移［7］。如图1所示，在RSSI算法模型中，节点随机运动，速率越大，定位偏差也越大，若简单地根据RSSI指纹数据库最近匹配原则计算节点位置势必产生较大误差。

　　有鉴于此，本文提出一种基于移动节点信号衰减渐变模型，利用极大似然估计算法思想将移动节点对周围RSSI指纹参量影响转变为概率事件，并通过泰勒级数修正渐变模型，推导移动速率对定位误差的关系和影响，既可以提高对移动节点定位的精确性，又可以弥补RSSI易受环境干扰的不足。

1极大似然估计算法

　　极大似然估计算法由德国数学家GAUSS C F提出，本质上是概率论在统计学中的应用［8］，目前已成为图2极大似然算法原理图无线传感网络测距算法之一，其概率统计定位原理如图2所示。

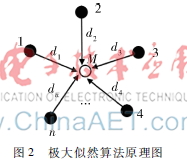
　　设目的节点M坐标为(x,y)，附近锚节点1，2，3，…，n的坐标分别为(x1,y1),(x2,y2),(x3,y3)，…,(xn,yn)，它们与节点M距离分别为d1，d2，d3，…，dn,则：

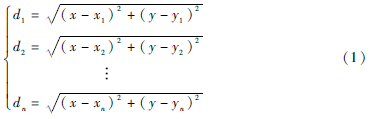
　　将式（1）转化为线性方程AX=B形式，有以下关系：

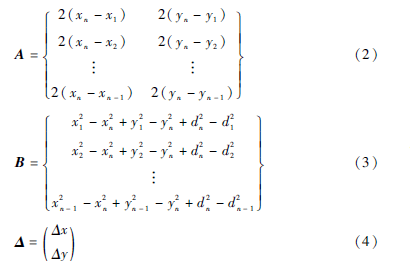
　　根据标准最小平均方差计算节点M坐标为:

　　X=(AT×A)-1×AT×B(5)

　　在上述定位过程中，极大似然估计算法通过周围节点概率统计分布估算节点M位置。本文利用该思想建立移动节点信号渐变衰减模型，将周围移动节点向量状态转换为对目的节点M的RSSI指纹参量的影响概率。

2新算法定位过程

　　2.1渐变模型

　　移动节点速率对周围信号波动和多普勒频移影响是一个渐变的过程［9］。各个节点信号参量以某种概率影响节点M的RSSI指纹参量。在渐变衰减模型中，距离d处信号强度是载波频率、节点移动速率、影响概率和衰减因子构成的复杂函数，表示为：

　　RSSI(dBm)=RSSI(d0)－10×n×lg10(ddf)+Q×v×∑Pn(6)

　　其中，RSSI(dBm)是节点接收信号参量，f为信号频率，d是实际距离，v为节点移动速率，Pn是来自移动节点n的影响概率，Q是修正参数。

　　2.2算法设计

　　泰勒级数是一种递归调用算法。由于移动节点速率对周围信号的影响是一个渐变过程，节点速率越大，对RSSI测量误差影响越大。新算法利用RSSI指纹参数值计算的距离信息和实际距离偏差递归校正概率影响参数Q,直到误差小于一定范围,结束递归调用，算法收敛。

　　设M为目的节点,测得其到周围锚节点参考距离为d1,d2,d3,…,dk，速率为v1,v2,v3,…,vk，利用极大似然估计法计算M(x,y)作为初始位置，fi(x,y)表示目的节点M到周围锚节点实际距离di之间的距离差值：

　　fi(x,y)=di－(xi－xd)2+(yi－yd)2－vi×t(i=1,2,3，…，n)（7）

　　将式（7）中距离节点M的初始距离M(xd,yd)和初始速率V(xv,yv)利用泰勒级数展开。为减少算法复杂性并计算影响概率Pn值, 舍去展开式高次项,得到式（8）:

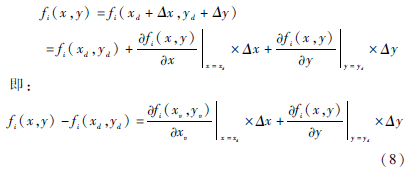
　　将式（8）转换为矩阵运算形式A*Δ=B，其中：

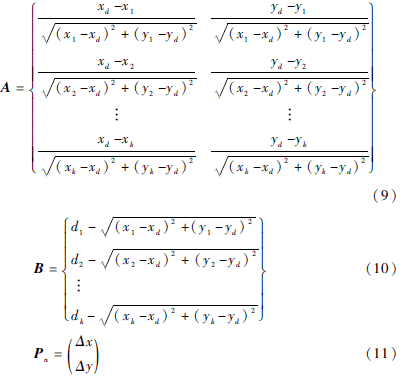
　　考虑节点移动速率对Pn的非线性影响，需施加权重因子Q并对A×Δ=B做加权矩阵修正。当加权矩阵Q为正定对角矩阵时：

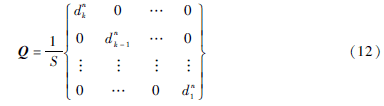
　　求线性方程A×Δ=Q×B的解：Δ=A－1×Q×B。

　　令:

　　xd=xd+Δx

　　yd=yd+Δy(13)

　　重复上述泰勒级数迭代过程, 直到|Δx|+|Δy|<ε,ε是偏差阈值，当校正量在阈值范围内结束迭代，计算修正参数Q。

　　2.3误差分析

　　假设目的节点M和锚节点i、n的实际距离分别为di^和dn^，估算距离分别为di和dn，则：

　　di^=di+di

　　dn^=dn+dn(14)

　　将n分别代入n和n-1项，计算n-（n-1）项有：

　　(di^)2－(dn^)=(di+di)2－(dn+dn)2(15)

　　得出目的节点M的平均定位误差为：

3仿真测试

　　3.1测试环境

　　将节点随机分布在100 m×100 m的网络区域，设最大锚节点数量为90，随机初始化节点移动状态并限制v0∈［0,5］,节点通信半径为20 m，利用MATLAB7.0软件对算法进行仿真比较。

　　3.2静态节点定位偏差测试

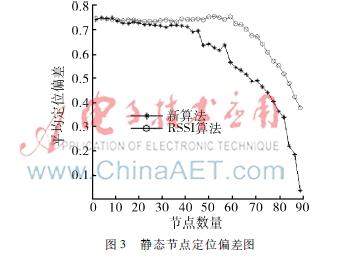
　　图3静态节点定位偏差图当节点速率为0时，两种算法定位偏差差别不大，在锚节点数量少于30个时两条曲线几乎重叠，如图3所示。这是由于节点数量较小，泰勒级数修正值几乎可以忽略不计。当节点数量大于60时，两种算法定位偏差急剧下降，算法差异明显。这是由于静止节点之间虽然不存在信号多普勒频移现象，但之间的信号波动和多径衰减影响依然存在，此时泰勒级数修正可以很好地弥补RSSI易受环境干扰的不足，对移动节点定位更加精确。

　　3.3动态节点定位偏差测试

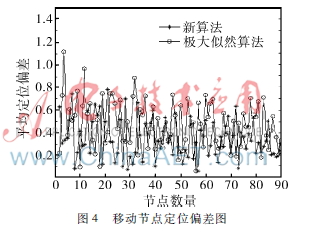
　　动态节点定位偏差测试结果如图4所示。由于新算法考虑到节点移动因素，利用泰勒级数修正节点运动对周围信号波动和多普勒频移的影响，其平均定位偏差比传统最大似然估计算法低约18.6%。另外，两种算法偏差都随节点密度的提高而逐渐减小，满足无线传感网络定位的共性，但新算法更具优势。

4结论

　　移动节点速率对周围信号波动和多普勒频移影响是一个渐变的过程，本文提出一种基于移动节点信号衰减渐变模型，利用极大似然估计算法思想将移动节点对周围RSSI指纹参量影响转变为概率事件，并通过泰勒级数修正渐变模型，减少节点移动对周围电磁环境的影响，有效弥补了RSSI易受环境干扰的不足。算法相对复杂，但定位结果更为精确。

　　参考文献

　　［1］ 曹晓梅,何欣,陈贵海.传感器节点定位系统攻防机制研究［J］.计算机科学，2008,35(7):3641.

　　［2］ 邓文莲.无线传感器网络节点定位的仿真研究［J］.计算机仿真,2012,29(5):167169.

　　［3］ 梅举,陈涤,辛玲.基于蒙特卡洛方法的移动传感网节点定位优化算法［J］.传感技术学报, 2013,26(5):689694.

　　［4］ 李锋.粒子群离散算法在无线传感网络中的应用［J］.微型机与应用,2014,33(12):5456,60.

　　［5］ 石琴琴,霍宏,方涛,等.使用最速下降算法提高极大似然估计算法的节点定位精度［J］. 计算机应用研究,2008,25(7):20382042.

　　［6］ 陈三风,陈万明.基于RSSI误差分析的无线传感器网络定位研究［J］.计算机工程与应用, 2011,47(14):1012.

　　［7］ 沈军,黄春华,罗护,等.基于RSSI优化的模型参数实时估计定位算法［J］.计算机工程与设计,2012,33(2):464468.

　　［8］ LAZOS L,POOVENDRAN R.HiRLoc:highresolution robust localization for wireless sensor networks［J］.IEEE Journal on Selected Areas in Communications,2006,24(2):233246.