谢玲1,2
(1.南京理工大学 紫金学院,江苏 南京 210046;2.南京大学 计算机科学与技术系,江苏 南京 210000)
摘要:BB84协议是目前最接近实用化的量子密钥分发(QKD)协议。点对点的量子密钥分发系统已经可以商用,但现有的多用户量子密钥分发协议都是采用量子纠缠、量子存储等技术手段进行密钥分发,在现有的技术条件下只能停留在理论阶段,离工程应用还有较长的距离。该文提出了一种基于BB84的多用户量子密钥分发协议,将计算机通信技术应用到量子保密通信中,实现一对多的量子通信网络的量子密钥分发,并从理论和实验结果两方面分析其可行性。
关键词:量子保密通信;量子密钥分配;多用户;BB84
0引言
当今世界,信息的安全至关重要,信息安全中最核心的技术是经典密码技术。自从Peter Shor在1994年提出了第一个具体的量子算法[1],RSA等基于大数质因子分解难题的公钥密码系统的安全性面临前所未有的挑战。量子保密通信特别是量子密钥分发技术(QKD)近年来得到了快速发展。
世界上第一个量子保密通信协议是BB84协议[2],由BENNETT C H和BRASSARD G在1984年提出。该协议使得经过认证的通信双方在两地能够连续建立密钥,进而通过OTP(一次一密乱码本)加密协议实现安全通信。BB84协议与经典密码体系中的基于计算复杂性的基本原理不同,它是以量子力学为基础,以“海森堡测不准原理”和“量子态不可精确克隆”这两个性质为原理,在历史上第一次提供了无条件安全性的方法,开辟了密钥分发和保密通信的新方向。BB84协议简单,可操作性强,其提出之后的20多年里,人们逐步完成了包括理想情况和各种现实条件下的安全性证明[310],进行了实验室的演示以及现有光纤和自由空间条件下的一系列工作。
然而,BB84协议虽然可以保证点对点通信双方获得安全密钥,但对于一对多的多用户通信来说,BB84协议适用性欠缺。原因在于BB84协议在通信过程中随机产生密钥串,导致接收端收到的密钥各不相同,随之而来的加密和解密的次数等同于接收端的数量。近年来,多用户QKD协议(MUQKD)得到了发展[11-17]。然而,这些MUQKD协议采用的技术手段如BELL基测量、量子存储和量子幺正变换,在现有的技术条件下只能停留在理论阶段,离工程应用还有较长的距离。
本文提出了一种多用户量子密钥分发协议,将计算机通信与量子通信理论相结合,在一对多的量子通信网络中,通信一次使接收端得到相互一致的密钥,从而使发送端只需对信息进行一次加密,即可将密文统一传送至各接收端。双方的密钥是在发送端产生的随机比特,采用BB84协议传输密钥,保证了密钥的安全性,且大大减少了发送端的加密次数。采用计算机仿真验证了该协议的可行性,使发展高速量子通信网络成为可能。
1BB84量子通信协议
BB84不仅是目前最接近实用化的量子通信协议,而且也是其他量子通信协议的基础。该协议描述如何利用光子的偏振态来传输信息进行量子密钥分发:发送方Alice和接收方Bob用量子信道(如果光子作为量子态载体,对应的量子信道就是传输光子的光纤)来传输量子态;同时双方通过一条公共经典信道(如因特网)比较测量基矢和其他信息交流,进而两边同时安全地获得或共享一份相同的密钥。公共信道的安全性不需考虑,BB84协议在设计时已考虑到了两种信道都被第三方 (Eavesdropper,通常称为Eve)窃听的可能。具体过程如下:
(1)Alice随机产生一个比特0或比特1,并且随机选取一对正交态基矢:“+”基或“×”基,从而将该光子制备成一个随机的量子偏振态,其中,0°偏振态记作|→>,90°偏振态记作|↑>,+45°偏振态记作|↗>,-45°偏振态记作|↘>。编码情况如图1所示。
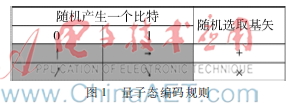
(2)Alice把制备在某个偏振态的光子通过量子信道传送给Bob,Bob接收到后开始测量该光子的量子态。测量时Bob并不知道Alice在制备量子态时选择了哪个基矢,只能随机选择一个测量基矢(“+”基或“×”基)来测量。测量过程中,Bob要记录对接收到的每个光子所选的基以及测量结果。
(3)Alice通过公共经典信号公布制备每个光子偏振态时所选择的基矢,Bob将测量对应光子时所选择的测量基矢与之进行对比,舍弃那些双方选择了不同基矢的比特(50%),剩下的比特还原并进行保存,从而完成密钥分发。此过程将有约一半的数据被筛选出来,留下的密钥称为原始密钥。原始密钥的形成过程如图2所示。

(4)双方随机公开一部分原始密钥用来估计误码率,并判断有没有窃听者Eve的存在。对于窃听者Eve来说,如果选择“+”基来测量|↑>,会以100%的概率得到|↑>,但是如果用“+”基来测量|↗>或|↘>态光子,结果就是随机的,会以50%的概率得到|→>或|↑>。也就是说,即使Eve选择的测量基与Alice的一样,都是“+”基,也无法分辨该光子原来的量子态是|↑>还是|↗>或|↘>(无法通过测量来彻底分辨非正交态)。然而一旦Eve对光子作了测量,就不可能完全克隆出原来被截获的光子。所以Eve的介入必然会额外增大错误率。若误码率在一定的阈值范围内,可以通过纠错技术进行纠错,然后对纠错后的密钥进行隐私放大,消除前面通信过程和纠错过程中导致的信息泄露,从而提取到无条件安全的密钥;若误码率超过一定的阈值,则放弃此次通信,通信双方选择新的量子信道进行量子密钥分发。
2基于BB84的多用户量子密钥分发协议
基于BB84的多用户量子密钥分发协议是针对一对多的量子密钥分发。如图3所示,假如有1个发送端,4个接收端,如果使用BB84协议,密钥分发过程需要4次,每次产生的密钥各不相同,所以发送端需要将信息分别加密4次,再将所得的密文分别传送至各个接收端。

在此基础上本文提出了多用户量子密钥分发协议。该协议工作过程如下:
(1)发送端随机产生n位二进制密钥串;
(2)将该密钥串重复m次得到N位密钥串;
(3)发送端随机选择基矢,将N位密钥串制备成相应的量子偏振态,然后经由量子信道进行传输;
(4)接收端随机选择测量基对接收到的量子态进行测量;
(5)双方通过经典信道进行基矢比对,保留基矢相同的部分,并告知发送端分组密钥长度n;
(6)基矢相同部分的量子态译码成相应的二进制比特,然后将每组(一共m组)保留下来的二进制比特按位进行拼接,得到一组与发送端相同的n位二进制密钥串。
(7)对多个用户进行密钥分发时重复上述过程,但n保持固定。如此完成一次量子密钥的分发。
采用此种协议的优势在于:
(1)经过一次多用户的量子密钥分发,发送端和多个接收端获得的密钥一致,发送端只需加密一次,即可将密文发送至各接收端,接收端规模越大,此优势越明显。
(2)一次多用户量子密钥分发过程产生的密钥是随机的,发送端和接收端随机选择制备基矢和测量基矢,保证了传输的安全性,当有窃听者存在时,误码率会增大,若误码率超过一定阈值,则放弃此次通信。
(3)在没有窃听者的理想情况下,经过基矢比对筛选后,通信双方的原始密钥应该是完全一致的。但是在现实系统中,由于非理想的物理器件和非完美的物理信道传输,会导致接收方的原始密钥有一定的误差,若误码率在一定的阈值范围内,则在接收端进行密钥拼接时按照少数服从多数的原则,可将每段中的错误信息剔除,最终得到与发送端一致的密钥串。
(4)分组密钥长度n和分组数m可根据接收端数据以及要加密的明文长度进行调节。
3理论和实验结果
3.1理论分析
对于分组密钥长度n和分组数m,设得到最终密钥的概率为p,计算可得:

当密钥长度固定时,可通过此公式选择合适的分组数m,使得p满足不等式:P>P0,其中,P0为得到一致密钥的最低阈值,保证各通信终端以极高的概率获取一致密钥。
3.2实验分析
对m和n取不同的值进行实验,统计密钥获得成功的概率。实验平台如图4所示。

其中,随机码位数为n,分组数为m,实验次数为接收端个数。
中间过程为模拟BB84工作过程,如图5所示。
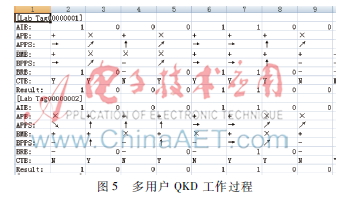
图5中,各参数意义如下:AIB为Alice生成的二进制随机比特;APB为Alice选择的基矢;APPS为Alice的量子偏振态;BMB为Bob的测量基;BPPS为Bob的量子偏振态;BRB为Bob接收的量子比特;CTB为对基结果,相同基为Y,否则为N;Result为拼接结果。
实验如下:
(1)取n=8,m为1~15,接收端数目为10 000,实验统计数据如图6所示。

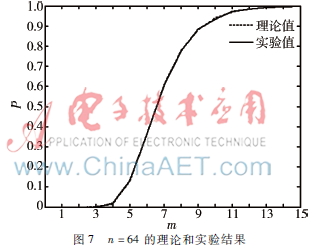
(2)取n=64,m为1~15,接收端数目为10 000,实验统计数据如图7所示。
(3)取n=128,m为1~15,接收端数目为10 000,实验统计数据如图8所示。

4结论
上述实验当分组数达到一定值时,即可以较大的概率得到一致密钥。而当分组数继续增大时,效果会变得不明显,且冗余信息较多。所以选择合适的分组数非常重要。
目前,量子保密通信尤其是量子密钥分发技术已成为具有重要战略意义的前沿技术之一,本文提出了一种基于BB84的多用户量子密钥分发协议,完成一对多通信网络的量子密钥分发,并用理论和仿真实验分析了其可行性。
参考文献
[1] SHOR P W. Algorithms for quantum computation: discrete logarithms and factoring[C]. Foundations of Computer Science, 1994 Proceedings, 35th Annual Symposium on. IEEE, 1994:124134.
[2] BENNETT C H, BRASSARD G. Quantum cryptography: public key distribution and coin tossing[C]. International Conference on Computer System and Signal Processing, IEEE, 1984:175179.
[3] SHOR P W, PRESKILL J. Simple proof of security of the BB84 quantum key distribution protocol[J]. Physical Review Letters, 2000, 85(2):441444.
[4] SCARANI V, BECHMANNPASQUINUCCI H, CERF N J, et al. The security of practical quantum key distribution[J]. Reviews of Modern Physics, 2009, 81(10): 13011350.
[5] LO H K, CHAU H F. Unconditional security of quantum key distribution over arbitrarily long distances[J]. Science, 1998, 283(5410): 20502056.
[6] MAYERS D. Unconditional security in quantum cryptography[J]. Journal of the ACM(JACM), 2001, 48(3): 351406.
[7] GOTTESMAN D, LO H K. Proof of security of quantum key distribution with twoway classical communications[J]. Information Theory, IEEE Transactions on, 2003, 49(2): 457475.
[8] RENNER R. Security of quantum key distribution[J]. International Journal of Quantum Information, 2005, 6(1): 1127.
[9] GOTTESMAN D, Lo H K, LTKENHAUS N, et al. Security of quantum key distribution with imperfect devices[J]. Quantum Information & Computation, 2002, 4(5):325360.
[10] KOASHI M, PRESKILL J. Secure quantum key distribution with an uncharacterized source[J]. Physical Review Letters, 2003, 90(5): 057902.
[11] Li Chunyan, Zhou Hongyu, Wang Yan, et al. Secure quantum key distribution network with Bell states and local unitary operations[J]. Chinese Physics Letters, 2005, 22(5): 10491052.
[12] Li Chunyan, Li Xihan, Deng Fuguo, et al. Efficient quantum cryptography network without entanglement and quantum memory[J]. Chinese Physics Letters, 2006, 23(11): 28962899.
[13] Deng Fuguo, Liu Xiaoshu, Ma Yingjun, et al. A theoretical scheme for multiuser quantum key distribution with N EinsteinPodolskyRosen pairs on a passive optical network[J]. Chinese physics letters, 2002, 19(7): 893896.
[14] Lin Song, Huang Chuan, Liu Xiaofen. Multiuser quantum key distribution based on Bellstates with mutual authentication[J]. Physica Scripta, 2013, 87(3): 035008.
[15] PHOENIX S J D, BARNETT S M, TOWNSEND P D, et al. Multiuser quantum cryptography on optical networks[J]. Journal of Modern Optics, 1995, 42(6): 11551163.
[16] BIHAM E, HUTTNER B, MOR T. Quantum cryptographic network based on quantum memories[J]. Physical Review A, 1996, 54(4): 26512658.
[17] XUE P, LI C F, GUO G C. Conditional efficient multiuser quantum cryptography network[J]. Physical Review A, 2002, 65(2): 130132.

