陈鹏旭

　　（西南科技大学 信息工程学院，四川 绵阳 621000）

     摘要：在实际获取远程观测图像的过程中，图像中经常夹杂了混合噪声。针对实际中一般由加性高斯白噪声（AWGN）和脉冲噪声（IN）所组成的混合噪声，提出了一种将剪裁中值滤波和基于加权编码图像稀疏表示相结合的混合噪声的去除算法。实验结果表明，所提算法在不同的噪声比率下都可以有较好的去噪表现，效果优于对比算法，而且能更好地保留纹理等细节。

　　关键词：混合噪声；中值滤波；稀疏表示；非局部相似；图像去噪

0引言

　　针对脉冲噪声的去除［1］，有递进开关中值滤波(Progressive Switch Median Filter，PSMF)［2］、对称剪裁中值滤波(Unsymmetric Trimmed Median Filter,UTMF)［3］等被提出。针对高斯噪声的去除，有传统的高斯滤波、非线双边滤波(Bilateral Filter，BF)、小波去噪［4］、字典学习和稀疏表示算法［5］。对于更加困难的IN和AWGN混合噪声的去噪［67］，有三边滤波(Trilateral Filter,TF)［7］、开关双边滤波(Switching Bilateral Filter,SBF)、RORNLM算法、非局部相似加权编码(WESNR)等。本文针对AWGN和IN(SPIN+RVIN)组成的混合噪声，经过将剪裁中值滤波初始去噪的非局部相似经验与加权编码结合，提出了一种有效的去噪算法。

1非对称剪裁中值滤波初始去噪

　　1.1噪声的模型

　　本文由AWGN、SPIN、RVIN所组成的混合噪声模型可以表示为：

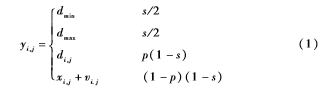
　　式(1) 中，噪声图像的灰度值为［dmin,dmax］。vi,j为方差是σ的高斯噪声值。s(0≤s≤1)是图像椒盐噪声的噪声比率，因为只可能是dmin或dmax，它们各为s/2。P为图像的随机脉冲噪声比，范围为［0,1］,对于在［dmin,dmax］的噪声点di,j，则yi,j=di,j的概率是p(1-s)。对于受高斯噪声污染的像素点值为yi,j=xi,j+vi,j，其概率为(1-p)(1-s)。

　　1.2剪裁中值滤波算法去噪

　　（1）如果要处理的像素点0<yi,j<255，就将其作为非噪声点保留，对下一个像素点进行处理，转向步骤（9）。

　　（2）否则，yi,j为噪声点。让其为中心，选定一个大小3x3的二维窗口。

　　（3）对窗口的所有非噪声点按照升序依次排序，放置于一维数组中，同时计算其元素个数n，若n为零，转向步骤（7）。

　　（4）n如果不为零，则对n进行奇偶判断。若n为奇数，则数组中间元素值为中值。

　　（5）若n为偶数，则数组中间的两个元素平均值为中值。

　　（6）获得中值替换处理的像素点yi,j，转向步骤（9）。

　　（7）如果Wi,j≤Wmax增大窗口，转向步骤（3）。

　　（8）当Wi,j>Wmax，如果j=1，则fi,1=fi-1,1；否则fi,j=fi,j-1。

　　 (9)重复执行步骤(1)，直到处理完整幅图像。

　　yi,j为坐标(i,j)上的像素值；fi,j为坐标(i,j)上处理后的像素值；Wi,j是初始大小为3×3以正在处理的噪声点为中心的滤波窗口；Wmax为允许的最大尺寸的窗口7×7。

2稀疏表示和非局部相似结合去噪

　　2.1去噪模型

　　图像用x来表示，用超完备字典Φ=［Φ1;Φ2;…Φn］对xi进行稀疏编码。通过最小二乘表示x为:

　　对于受到高斯噪声所污染的图像y，要得到期望α，其模型应为:

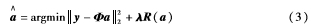
　　式(3)用l2范数来代表数据的拟合残差。让数据保真项残差的分布与高斯噪声下残差的分布设置为相似的话，则l2范数对于混合噪声下的编码残差依然适用。

　　为了削弱混合噪声的重尾现象，对每一项残差设计一个权重，则：

　　新的混合噪声去噪模型:

　　式(6)为去噪模型。为了达到更好的效果，这里将其图像的先验知识运用于R（α）的设计中，这样构建的去噪模型获得的稀疏表示系数会更为准确。

　　用∑iai-μilp作为正则项代入式(6)中。

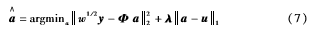
　　2.2模型的求解

　　w确认后，式(7)所表示的模型就变成l1范数稀疏编码模型。本文设V为一对角线矩阵，通过k+1次迭代时，V中元素更新为：

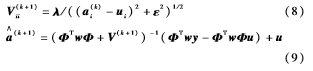
　　希望的稀疏表示系数a通过V与a的迭代更新获得。

3实验结果与分析

　　本文方法的实验平台为MATLAB 2012a，计算机配置为3.2 GHz Inter(R) Core(TM)i53470CPU以及4.0 GB内存。如图1“Lake”、“Dune”、“Fall”、“Long”、“Island”和“Tree”6幅图像作为测试图像。

　　选用的“Lake”图像在σ=0.1,r=0.05,s=0.5（σ为标准差，r为RVIN噪声比率，s为SPIN噪声比率）的情况下，通过典型的混合噪声去除算法与本文算法去噪后所得到的图像效果，如图2所示。

　　从图2可以看出，本文算法相对其他几种混合噪声去噪算法，去噪效果更优。

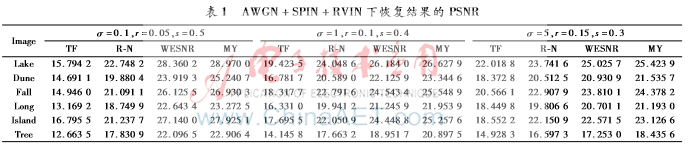
　　用PSNR和FSIM衡量去噪后效果，对6幅图像在由AWGN+SPIN+RVIN所组成的不同噪声比率情况下，得到的数据如表1所示。

　　通过表1可以看出，本文提出的方法得到的结果高于其他几种混合噪声去除算法的PSNR、FSIM值，说明了所提出的算法去噪效果更好。

4结束语

　　针对加性高斯白噪声（AWGN）和脉冲噪声（IN）所组成的混合噪声，本文通过改进非对称剪裁中值滤波对噪声图像进行了初始去噪，进而用基于加权编码稀疏表示和非局部相似经验相结合的算法，对脉冲噪声和高斯噪声同时进行处理，最终得到去噪图像。

　　参考文献

　　［1］ 阮秋琦.数字图像处理［M］. 北京:电子工业出版社,2005.

　　［2］ BOO I H， TOH K K V. An improved progressive switching median［C］.Filter in Future Computer and Communication, 2009. ICFCC 2009. International Conference on , 2009: 136 139.

　　［3］ SHARMA S, YADAV P. Removal of fixed valued impulse noise by improved trimmed mean median filter［C］. in Computational Intelligence and Computing Research (ICCIC), 2014 IEEE International Conference on , 2014: 120.［4］ 刘炳良. 一种小波域改进双边滤波的水果图像去噪算法［J］. 红外技术,2014,36(3):196 199,204.

　　［5］ 孙君顶,赵慧慧. 图像稀疏表示及其在图像处理中的应用［J］. 红外技术,2014,36(7):533537.

　　［6］ GARNETT R, HUEGERICH T, CHUI C, et al. A universal noise removal algorithm with an impulse detector ［J］. IEEE Transactions on Image Processing, 2005,14(11): 1747 1754.

　　［7］ XIONG B, YIN Z P. A universal denoising framework with a new impulse detector and nonlocal means ［J］. IEEE Transactions on Image Processing, 2012, 21(4): 1663 1675.