吉哲1,2，傅忠谦1

　　（1.中国科学技术大学 电子科学与技术系，安徽 合肥 230027； 2.海军蚌埠士官学校 二系，安徽 蚌埠 233012）

      摘要：柴油机声信号包含了丰富的运行状态信息，为了能有效地提取特征参数，需要对柴油机声信号进行去噪处理。针对传统小波阈值去噪和经验模态分解（EMD）去噪的不足，提出了一种将小波阈值与EMD相结合的去噪方法。借助EMD的自适应分解特性，在原始信号分解的基础上，利用相关系数法确定信号主导和噪声主导本征模函数（IMF）分量的分界点，将改进的小波阈值函数对噪声主导的IMF分量进行阈值去噪，再进行信号重构。仿真实验和实测结果表明，该方法去噪效果更优，适合非线性非平稳信号去噪，能够保留柴油机声信号的原貌特征。

　　关键词：小波变换；EMD；阈值函数；去噪处理

0引言

　　柴油机作为一种重要的动力机械，广泛应用于工业、农业、交通、军事等各个领域。柴油机的声信号包含着丰富的信息，对信号进行特征提取可以进一步分析设备的运行状态，为故障诊断提供特征参数。由于柴油机声信号在采集过程中不可避免地混入各种噪声，影响了真实信号的提取，所以必须去除干扰噪声的影响，实现信号去噪。柴油机结构十分复杂，噪声激励较多，其声信号是典型的非平稳非线性时变信号，频率成分十分复杂［1］ ，属于宽频谱信号。由于无法事先确定柴油机声信号的滤波频率，不易严格按周期采样，传统的去噪方法如谱分析、信号滤波、时域分析技术等难以发挥作用。小波分析作为新的时频分析工具，具有良好的自适应性，并迅速应用到信号去噪中［2］。参考文献［3］、［4］提出了一种改进的小波阈值，弥补了硬阈值存在不连续性和软阈值存在恒定偏差的缺点。经验模态分解（Empirical Mode Decomposition，EMD）是一种基于数据驱动的分解方法，避免了小波分解中基函数和分解层数选择困难的问题。参考文献［5］将EMD应用到柴油机振动信号的去噪处理中，取得了较好的效果。参考文献［6］将小波阈值与EMD相结合，对每一个IMF分量设定一个阈值进行门限处理，再将去噪后的IMF分量进行重构，实现信号去噪，效果优于传统的小波阈值去噪。本文进一步改进了小波阈值函数，并结合EMD进行阈值去噪研究，通过实验证明了该方法的有效性。

1小波阈值去噪

　　信号去噪是小波变换的重要应用之一，主要有基于模极大值去噪、小波系数相关性去噪、小波阈值去噪、平移不变量去噪等几种方法。其中DONOHO DL［2］提出的小波阈值去噪是工程中应用最广泛的方法。

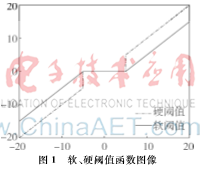
　　阈值函数的选择是小波阈值去噪过程中的关键步骤之一，常用的阈值函数有硬阈值和软阈值，函数图像如图1所示。在实际工程中，这两种方法得到了广泛的应用，取得了较好的效果。

　　硬阈值：

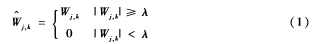
　　软阈值：

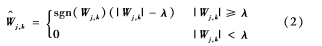
2EMD相关系数法去噪

　　在基于小波的去噪过程中，基函数和分解层数的选择主观性较强，而且小波方法的一个限制是基函数固定，因此不一定匹配所有真实的信号。一旦选择了小波基，必须使用它分析整个数据。而EMD方法直接来源于信号本身，无需先验基底，作为自适应时频分析的一种方法，避免了小波分解中小波基和分解层数的选择困难，非常适合非平稳、非线性信号的分析。EMD方法将原信号分解为若干个本征模函数（IMF）和一个残余函数之和。经验模态分解具体处理过程见参考文献［7］。

　　信号经过经验模态分解可以得到频率由高到低的一系列IMF分量。信号的噪声主要分布在高频段，也就是前几阶的IMF分量，而信号则主要分布在后几阶的IMF分量［8］。因此，只要找到噪声主导的IMF分量与信号主导的IMF分量之间的分界点，将噪声主导的IMF分量舍弃，再将其余的IMF分量和残余分量进行信号重构，就可以达到去噪的目的。EMD去噪是基于分解信号的部分重构，记为EMDPR（EMDPartial Reconstruction），去噪后的信号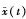为：

　　Pearson线性相关系数是用来衡量两个变量之间线性相关程度的指标，通过比较各阶IMF分量与原信号的相关系数可以确定噪声主导与信号主导IMF分量的分界点kth，这里的相关系数定义为：

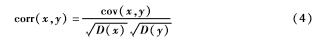
　　其中，cov(x,y)为x和y的协方差，D(x)为x的方差，D(y)为y的方差。在这里，x代表原始信号，y代表各阶IMF分量，得到公式(5)：

　　分别计算各个IMF分量与原信号的相关系数，得到参数L：

　　通过相关系数曲线，找出曲线中第一个局部极小值点，将此点对应阶数的下一阶作为噪声主导与信号主导IMF分量的分界点kth，表示为：

　　此时，将前kth－1阶IMF分量作为主要噪声滤除，从第kth阶IMF分量到残余分量进行信号重构，便得到去噪后的信号。

3小波EMD去噪算法

　　3.1改进小波阈值函数

　　由于小波软硬阈值本身存在着一定的缺陷。由硬阈值方法得到的估计小波系数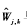在λ处是不连续的，重构后的信号可能会出现振荡。由软阈值方法得到的估计小波系数W^j,k与Wj,k总存在恒定的偏差，将直接影响重构信号与真实信号的逼近程度，带来不可避免的误差。为了弥补软、硬阈值的不足，参考文献［4］提出了一种改进的阈值函数：

　　其中,u=1－e－α(|wj,k|－λ)2，且α为正数。

　　该阈值具有调节因子，且解决了连续性问题，但小波系数与估计小波系数仍存在恒定的偏差。本文在此基础上进一步改进，设计了一种新的改进阈值函数，函数图像如图2所示。

　　改进阈值函数为：

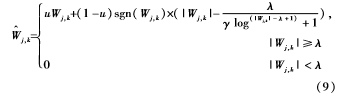
　　其中,u=1－e－α(|wj,k|－λ)β，α、β、γ为正数。函数在λ处是连续的，并且以W^j,k=Wj,k为渐近线。当Wj,k→∞时，W^j,k逐渐接近Wj,k，解决了小波系数与估计小波系数之间存在恒定偏差的问题。阈值设置为分层阈值，随着分解尺度j的增加，阈值λ逐渐减小，符合噪声在小波分解各层分布的情况，如式(10)所示。

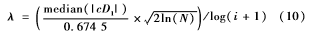
　　此外，当α=0、γ=0时，阈值函数变为软阈值；当α→∞时，阈值函数变为硬阈值。可见，该阈值可根据实际应用进行调整,十分灵活。

　　3.2算法流程

　　含噪信号经过经验模态分解后，低阶IMF分量中虽然噪声占主要成分，但是仍然含有有用信号，信号和噪声的频带通常是交互存在的。如果将前几阶的IMF分量强制舍弃，必会造成信号完整性的破坏。因此，本文利用小波阈值函数对前几阶的IMF分量进行阈值处理，算法流程如下：

　　（1）对原信号进行经验模态分解，利用相关系数法确定噪声主导与信号主导IMF分量的分界点kth；

　　（2）将前kth－1阶IMF分量利用改进的小波阈值函数进行阈值化处理；

　　（3）把阈值化后的IMF分量和剩余IMF分量及残余函数进行信号重构。

4仿真实验分析

　　在实际工程中，一般很难获得机械设备的纯净信号，为了验证本文所提出的去噪算法对柴油机声信号的去噪能力，分别选取三种谐波仿真信号进行去噪实验。仿真信号解析表达式为：

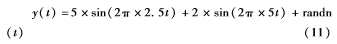
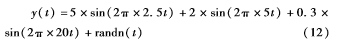
　　仿真信号由调频调幅信号和高斯白噪声叠加而成，高斯白噪声信噪比设为12 dB，调频调幅信号随着调制频率的升高幅值逐渐下降，符合柴油机声信号的特点。

　　式(11)记为仿真信号1，式(12)记为仿真信号2，式(13)记为仿真信号3。以仿真信号1为例，对含噪信号进行经验模态分解，分解结果如图3所示。IMF1~IMF8为第一阶至第八阶本征模函数，RES为残余函数。

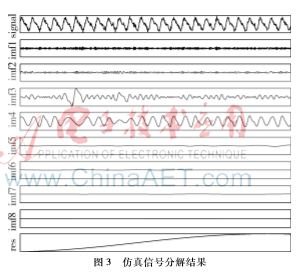
　　分别计算各阶本征模函数与原信号的相关系数，其变化曲线如图4所示。

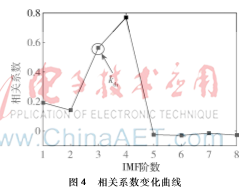
　　从图4可以看出，曲线第一个局部最小值出现在第二阶的位置，kth值为3。将前两阶本征模函数进行改进小波阈值处理，阈值设为分层阈值：

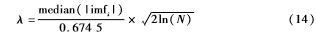
　　把阈值化后的IMF分量和剩余IMF分量及残余函数进行信号重构便得到去噪后的信号。为了验证该去噪算法的性能，利用信噪比（SNR）和均方根误差（RMSE）对比相关去噪方法的去噪效果。其中:

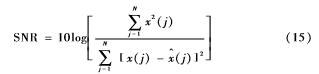
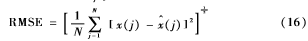
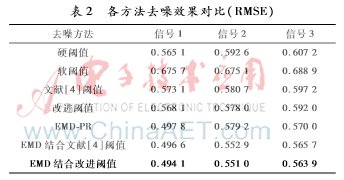
　　参数设置为：α=8,β=5（小波去噪）,β=2（EMD去噪）,γ=10，根据文献［9］应用各种小波基进行阈值去噪的评价结果，确定小波阈值去噪的小波基为sym12，分解层数为4层。去噪效果对比如表1和表2所示。

　　从表1和表2中可以看出，本文提出的去噪方法在三种仿真信号去噪实验中均有较好的表现，信噪比有所提高，同时均方根误差下降，发挥了小波阈值去噪和EMD去噪各自的优点。　　

5实际应用

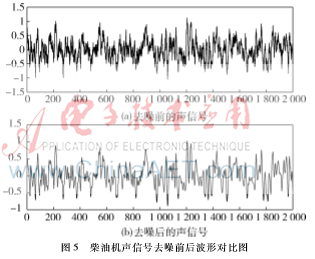
　　实验选取6135D型柴油机，转速设为1 300 r/min，采集位置为缸盖上方50 cm处，以44.1 kHz采样频率采集柴油机空载正常工作时的声信号数据。应用本文提出的去噪方法对含有高斯白噪声的柴油机声信号进行去噪处理，从图5中可以看出，该方法能够较好地去除噪声，且保持了原信号的细节信息。

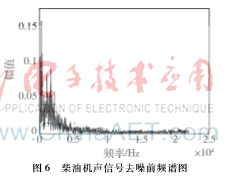
　　由图6和图7可以看出,柴油机原始声信号频率分布散乱，充满整个频率坐标轴。去噪后，0~5 kHz区间保留了声信号的原貌特征，8 kHz以上频段信号频谱值大幅减少，去除了高频噪声，保留了信号的有用频段。

6结论

　　在传统小波阈值去噪和EMD去噪的基础上，提出了一种EMD与小波阈值相结合的去噪方法，并设计了改进的阈值函数。新阈值具有调节因子，通过改变参数，可以得到最佳的小波阈值估计。实验结果表明，该去噪算法有着更好的去噪效果。应用到实际柴油机声信号去噪处理中，去噪信号能够真实反映原信号的特征，为提取特征参数起到了信号预处理的作用。

　　参考文献

　　［1］ 徐红梅，郝志勇,杨陈，等.基于EMD和HHT的内燃机噪声信号时频特性研究［J］.内燃机工程，2008，29(6)：6064.

　　［2］ DONOHO D L.Denoising by softthresholding［J］.IEEE Transaction on Information Theory，1995，41(3)：613627.

　　［3］ 唐进元，陈维涛,陈思雨，等.一种新的小波阈值函数及其在振动信号去噪分析中的应用［J］.振动与冲击，2009，28(7)：118121，217.

　　［4］ 张莲，秦华锋，余成波.基于小波阈值去噪算法研究［J］.计算机工程与应用，2008，44(9)：172173.

　　［5］ Tan Jiqiu, Min Jie, Wu Xin.Diesel engine fault diagnosis and denoising disposal of the vibration signals based on EMD method［C］.2013 Fourth International Conference on Digital Manufacturing & Automation,2013：488491.

　　［6］ 籍永建，王红军.基于EMD的主轴振动信号去噪方法研究［J］.组合机床与自动化加工技术，2015(5)：3537.

　　［7］ HUANG N E,SHEN Z,STEVEN R L,et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceding of the Royal Society Lond,1998,454(8):903995.

　　［8］ Pei Yao, Wu Yangang, Jia Dacheng. Research on PD signals denoising based on EMD method［J］.Przeglad Elektrotechniczny,2012,88(1):137140.

　　［9］ BASKAR V V, RAJENDRAN V, LOGASHANMUGAM E.Study of different denoising methods for underwater acoustic signal［J］.Journal of Marine Science and Technology,2015, 23(4):414419.