刘燕1，何明亮2，姚建国1,3
(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003;2.上海贝尔股份有限公司 无线产品部，江苏 南京 210003;3.南京邮电大学 江苏省无线通信重点实验室，江苏 南京 210003)
摘要：导航接收机常工作于复杂的电磁环境下，易受到电磁等干扰，导致其导航定位功能的精确度降低。针对这一问题，提出了空时自适应干扰抑制算法。该算法在不增加阵元的前提下，通过时间抽头来增加天线阵列的自由度，由此增加可处理干扰的数目，增强对宽带干扰和窄带干扰的抑制能力。通过MATLAB仿真验证了该算法的有效性。
关键词：北斗导航接收机；空时自适应；干扰抑制算法；MATLAB仿真
0引言
北斗导航系统是我国自主研制的卫星导航系统，用于现代科技、军事等各个领域。导航接收机常工作于复杂的电磁环境下，易受到电磁等干扰［1］，虽然其本身具有一定的抗干扰能力，但由于抑制宽带干扰所需的自由度比窄带干扰信号要多，传统阵列信号处理不能很好地对宽带干扰进行有效抑制，因此提出了空时自适应算法。该算法是将传统的空域和时域抗干扰算法相结合，在不增加阵元的前提下，通过增加时间抽头来提高天线阵列的自由度［2 3］，从而增强卫星导航接收机的抗宽带干扰的能力，使其能在复杂的电磁环境下发挥重要作用。
1空时自适应滤波技术
空时自适应滤波建立在空域滤波的基础上，结合了空域和时域滤波两种算法，在不增加天线阵元的前提下，在已有的天线阵列后加上若干个延迟单元，从而增加可处理干扰的数目，增强对宽带干扰和窄带干扰的抑制能力。从每个阵元通道来看，各级延时相当于时域滤波器，可以在时域滤除干扰；从相同的延时节点看，不同的阵元构成了空域的自适应滤波，可以分辨不同空间分布的干扰源［4 7］。
空时自适应算法系统框图如图1所示。
信号进入天线后，经过HPF（高通滤波器）进行去直流处理，然后将去直流后的信号送入一个NCO（数控振荡器），NCO将送来的有效频谱搬移到基带，接着接入一个FIR低通滤波器，将带外干扰滤除，再将一系列处理后的信号进行空时处理，最后将处理后的信号送入接收机。
设阵元数为M，延迟单元数为P，每个时间延迟单元的时间间隔为T，空时自适应干扰抑制算法模块图如图2所示。
经过一系列处理过的信号进入后，第k个阵元的第j个抽头接收到的信号为：
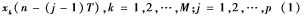
其中，M表示阵元个数；k表示每个天线的延迟单元数；T表示每个抽头的延时。
假设第k个阵元的第j个抽头的权值为w，输出y可以表示为：
写成矩阵型式：
式中，定义权向量：
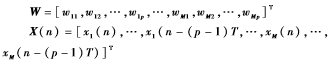
再将W和X(n)表示为:
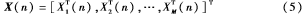
其中，
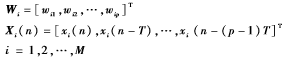
令d(n)表示所期望的输入信号，定义误差信号e(n):
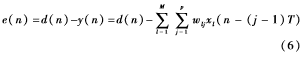
将误差信号写成矩阵形式，即为:
误差信号平方为
等式两边取数学期望，即得均方误差:
定义互相关函数:
自相关函数:
则误差函数可表示为:
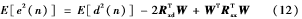
由上述公式可知，误差函数是权系数W的二次函数，且是一个上凹的抛物面，由此可知，误差函数存在最小值，使误差函数取最小值的权系数即为最佳。
根据二次函数求最小值的方法，对误差函数求导数（梯度），即可求得最佳权系数。因此，对均方误差求梯度为：
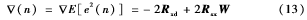
令(n)=0，则求得最佳权系数
令L(n)=E［e2(n)］，要求出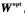
，需要知道
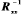和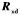
的值。采用最速下降法，设权值向量的初值为W(0)，沿L减小的方向调整W［8］。用下面的式子来调整W，使其无限接近Wopt。
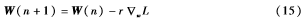
其中，r表示步长因子，取正值。
用梯度估计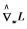
代替
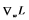，则
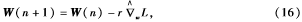
梯度估计表示为：
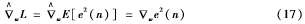
即用瞬时误差梯度来估计均方误差梯度，式中，
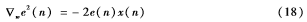
将式(18)带入式(15)，则权值更新公式为：
2空时自适应算法性能仿真分析
前面研究了空时自适应干扰抑制算法，下面用MATLAB对该算法进行仿真分析，仿真条件如下：天线阵列数为4，天线每个抽头的延时为1，天线的延迟单元数为8；实验频点：B3频点，干扰数：3，干扰强度：65 dB，输入信号：4路，输入信号频率：1 268.52 MHz，输出中频信号的中心频率：46.52 MHz。
图3表示输入信号的幅度和频谱。
图4表示的是经空时滤波之后的信号的幅度和频谱，容易看出，由于干扰的存在，在进行空时自适应干扰抑制之前，对于同一采样点而言，干扰信号的幅度相对较大，经过空时自适应干扰抑制后，干扰信号的幅度有较为明显的降低。并计算得相消比为22.48 dB。这说明，空时自适应干扰抑制算法对干扰有显著的抑制效果。
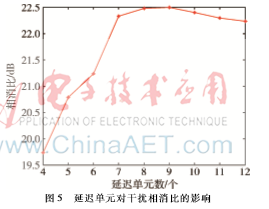
表1对不同的延迟单元数对应的相消比进行了归纳。图5表示不同的延迟单元数对应的相消比，从图中可以看出，随着延迟单元数目的增加，相消比相对增加了，达到某个延迟单元数时，相消比会达到一个最优值，之后，随着延迟单元数的增加，相消比不但不增加，反而略微地下降。
因此，根据此次的研究数据可知，随着延迟单元数的增加，频率的分辨率越来越高，窄带干扰形成的零点会越来越窄，部分频带干扰所形成的零点范围也越来越接近真实频率范围，所以相消比会越来越大，但由于自身性能的限制，延迟单元数达到一定值后，相消比已达到最上限，之后再增加延迟单元数，相消比改善并不明显，反而有略微的减小。由此可知，不同的干扰源和干扰数目，适当的延迟单元数，对干扰的抑制也很重要。
3结束语
本文对空时自适应算法进行了研究和分析，并用MATLAB对算法进行了仿真，结果表明，空时自适应算法在不增加阵元的前提下，通过时间抽头来增加天线阵列的自由度，能够增加可处理干扰的数目，有效抑制干扰。
参考文献
［1］ 王晓君，张伟，杜萌萌. 北斗卫星导航系统的应用及其抗干扰技术［J］.河北科技大学学报，2014，31(3):234 238.
［2］ 姚锐. 北斗接收机空时联合抗干扰算法研究［J］. 西安电子科技大学学报，2015，28(1):147 149.
［3］ 黄喆. 北斗接收机的空时二维抗干扰算法的研究与实现［D］. 成都：电子科技大学，2014.
［4］ 翟永刚. 导航接收机空域自适应干扰抑制技术研究及实现［D］. 成都：电子科技大学，2009.
［5］ 卢丹，冯青，吴仁彪. 基于空时自适应处理的GPS宽带干扰抑制技术［J］. 中国民航大学学报，2007， 25(4):672 674.
［6］ 吕翠改. 基于空时域的北斗导航抗干扰接收算法研究［D］. 石家庄：河北科技大学，2013.
［7］ FANTE R L, VACCARO J J. Wideband cancellation of interference in a GPS receive array［J］.IEEE Transactions on Aerospace and Electronic Systems,2000, 36(2): 549 564.
［8］ 俞志斌. 基于空时联合的卫星通信系统抗干扰性能研究［D］. 哈尔滨：哈尔滨工业大学，2009.