0 引言

    医学细胞图像分割的传统方法主要有基于区域的分割方法和基于边缘的分割方法，后者主要包括：边缘检测法^[1，2]、基于形变模型的方法^[3，4]和链码法^[5-7]。

    链码是用曲线起点坐标和边界点的方向编码来表示图像边界的一种编码方法，常用于图像处理、计算机图形学和模式识别等领域。基于链码法的图像分割一般采用5个步骤：边界检测、链码统计、拐点判断、分割点筛选和线性插值分割。实现细胞图像的有效分割需满足3个条件：(1)完整清晰的细胞边缘；(2)真实分割点的判断；(3)消除细胞小粘连（细胞上小黑点）和多细胞粘连分割。

    陆宗骐等^[5]通过计算每个边界点的链码差来判断轮廓的凸凹角点，并结合曲率半径和等效周长等特征参量实现细胞分割，该方法分割效果较好，但存在计算量大、分割速度慢的问题。牛庆肖等^[6]将链码和小波变换相结合提出一种新的轮廓描述方法，但由于边界函数的一维小波变换对边界起点较敏感，导致算法的不变性较差。张宇等^[7]通过分析分水岭算法，并借鉴链码思想来实现细胞分割，实验结果表明：带标记的分水岭可有效避免过分割情况，然而对标记的提取需要使用者具备一定的医学知识，另外，当标记落在细胞边界时，检测到的边界会包含少量的伪边缘点和孤立点。

    本文在前期研究基础上^[8]，提出了一种ECCC(Eleven Components Chain Code)链码分割算法，实现对医学细胞图像的快速分割。实验结果表明，算法的分割速度快、精确度高，在复杂的细胞图像分割中具备一定的有效性和可行性。

1 ECCC链码

    白细胞和神经元干细胞是两种常见的类椭圆形医学细胞。本文提出一种新的链码模型ECCC，ECCC是针对类椭圆形细胞的链码分割方法，在Freeman链码（8方向）中插入了3个新的链码元素“S”、 “8”和“9”。有别于传统链码模型需要对每个边界点计算链码差来判断轮廓的凸凹角点，并结合曲率半径和等效周长等特征参量实现细胞分割，新算法只需对ECCC编码中的链码元素“8”计算链码差就可判断真实分割点，大大提高了分割速度和精确度。

    具体编码过程为：

    (1)定位起始点“S”。按从上到下、从左到右的顺序扫描细胞边界，第一个遇到的像素点即为起始点，记作链码“S”。

    (2)检测边缘拐点并定位。从“S”开始按逆时针方向跟踪边界，当两个相邻边界点的链码方向相反时，比如前者的方向向上(正上、右上和左上)而后者的方向向下(正下、右下和左下)或者前者的方向向左(正左、下左和上左)而后者的方向向右(正右、下右和上右)时，在变换点处标记元素“8”。

    (3)定位末端点“9”。将边界点中y值最大的像素点记作末端点“9”，若有几个点的y值均为最大值，取x值最小的点。

    (4)链码跟踪。由起始点“S”跟踪轮廓一周至轮廓闭合，当起点和终点的链码方向一致时结束。

    定位图1(a)的起始点“S”是按从上到下、从左到右的顺序，从“S”开始沿逆时针方向跟踪边界至起始点，轮廓闭合，也可按从下到上、从右到左的顺序。两者的跟踪方式相同，区别在于扫描的起点和顺序。图1(b)的Freeman链码是55567760011223234，ECCC编码后为S55568776900112283234，如图1(c)所示。

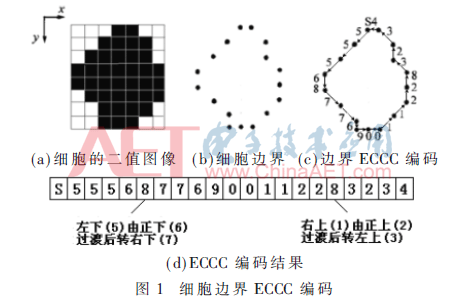
2 ECCC分割和计数方法

    细胞边界ECCC编码，记录其中链码元素“8”的个数，针对白细胞和神经元干细胞轮廓的类椭圆形特点，筛选真实分割点和进一步的细胞分割及计数。

    统计120张细胞图像的ECCC编码，结果显示，“S-9” 或“9-S”中仅会出现一次“8”，这表明x值最小的边界点有一次由左至右的方向变化或者x值最大的边界点有一次由右至左的方向变化。

    可采用下式对细胞计数：

其中，Q、n分别是细胞和链码“8”的个数，若Q为小数则进位取整。一般单个细胞的ECCC编码包含2个“8”点，2粘连细胞的编码中包含6个“8”点。统计120张细胞图像的ECCC编码，结果显示：每增加1个粘连细胞就会增加4个“8”点，因此粘连细胞ECCC编码中链码“8”的个数为4(Q-1)+2。另外，细胞图像往往存在图像对比度低和细胞边缘模糊的情况，实验结果表明，除数取4可以较好地减少这些干扰，确保计数结果的准确性。

    细胞图像的粘连以2细胞和3细胞粘连居多，图2和表1显示了白细胞图像的ECCC简码(将编码中的重复链码进行精简)及分割结果。图2(b)和图2(f)的ECCC编码中链码“8”均出现6次，由式(1)可知为2粘连细胞；图2(j)、图2(n)的ECCC编码中链码“8”均出现10次，由式(1)可知为3粘连细胞。对120幅白细胞图像进行计数，准确率可达98%。

    由图2(a)、(e)、(i)和(m)可知，分割点均为边缘凹角点，只有快速准确地定位这些角点才能实现实时有效的细胞分割。如图2(b)、(f)、(j)和(n)所示，链码“8”除位于分割点外，还有少量在细胞轮廓的光滑部分。对细胞图像ECCC编码后，本文采用链码差来检测拐点“8”中的分割点。由于不需要对每个边缘点都采用链码差来判定其凸凹性，该算法相比于传统链码模型减少了近55%的计算量。

    采用下式计算链码差Diff^[5]：

式中，Sum(i)为当前点的链码和，当采用逆时针方向跟踪边界时，凸凹角点的链码差分别取负值和正值。

    本文检测拐点“8”中分割点的方法为：

    链码和将圆周均分为24份，其值相差1，意味着相差15°。细胞分割点均为边缘凹角点，凹角点的链码差取正值，值为3说明角度变换45°。

    采用式(3)来检测链码“8”中的分割点，如图2(c)、(g)、(k)和(o)所示，检测结果准确无误。最后，对分割点线性插值，如图2(d)、(h)、(l)和(p)，粘连处得到有效分割。

3 实验结果及分析

    实验是在MATLAB 8.0的编译环境中，在Pentium D CPU 2.8 GHz、内存2.96 GB的PC上进行。分别采用ECCC和传统链码模型对120张白细胞和神经元干细胞图像（两类细胞图像各60张）进行分割检测。由于篇幅限制，仅显示其中两张典型细胞图像的分割结果，如图3、4所示。

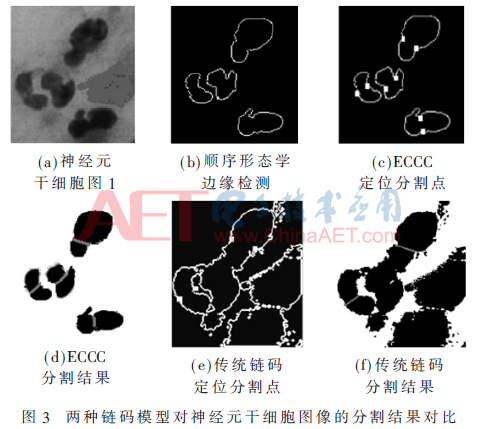
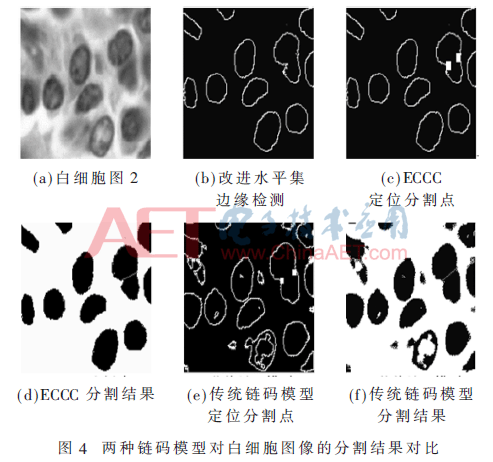
    对图3(a)、4(a)采用所提出的两种边缘检测方法^[8]得到完整、连续的细胞边界，如图3(b)、4(b)。细胞边界ECCC编码并检测链码“8”中的分割点，如图3(c)、4(c)，分割点的定位误差分别为1.01、1.23个像素。传统链码模型存在边缘检测精度低和分割点漏检的问题，如图3(e)、4(e)所示，分割点定位误差分别为9.32、2.65个像素。医学细胞图像具有对比度低、细胞边缘模糊的特点，传统链码模型在跟踪边界时易将噪声点和模糊处误判为边界，从而出现了一些伪边缘点，这对下一步的分割造成较大影响。

    本文采用分割点定位误差^[9]来定量比较两种链码分割法的精确度，结果如表2所示。设算法检测的分割点集合为CDET，手工定位的分割点集合为CRET，最大距离误差设为D_max=3，对于有d_ij=||C_i-C_j||，若d_ij≤D_max，则C_j、C_i配准，否则C_j为错误分割点，d_ij的均值为定位误差。由表2可知，ECCC检测分割点更准确。

    表3对比了两种链码模型的运行时间，可见，ECCC减少了近55%的计算量，分割速度更快。对大量类椭圆形医学细胞图像进行分割测试，实验结果表明：在分割精度上，ECCC高于传统链码模型；在运行时间上，ECCC的优势更明显。

4 结论

    本文针对类椭圆形细胞，提出了ECCC链码分割方法，新算法在Freeman链码中插入了3个新的链码元素“S”、“8”和“9”。有别于传统链码模型需要对每个边界点计算链码差来判断轮廓的凸凹角点，并结合曲率半径和等效周长等特征参量实现细胞分割，新算法只需对ECCC编码中的链码元素“8”计算链码差就可判断真实分割点。对大量2粘连和3粘连细胞图像进行分割测试，实验结果表明：ECCC法的分割成功率分别为100%和98%，平均耗时分别为0.42 s和0.67 s，比传统链码分割法减少了近55%的计算量，在复杂的细胞图像分割中具备一定的有效性和可行性。

参考文献

[1] HUO G Y.Edge detection for gastric cancer cell images based on improved sobel operator algorithm[J].Pattern Recognition Letters，2012，25(6)：603-618.

[2] ZHANG H，DA F P，LIH Q，et al.Methods of edge location for ellipse[J].Optical Technique，2013，36(1)：66-74.

[3] 宋效东，汤国安，周毅.基于并行GVF Snake模型的黄土地貌沟沿线提取[J].中国矿业大学学报，2012，42(1)：142-150.

[4] BRESSON X，ESEDOGLU S，VANDERGHEYNSE P.Fast global minimization of the active contour snake model[J].Advances in Intelligent and Soft Computing，2013，28(4)：151-167.

[5] 陆宗骐，童韬.链码和在边界形状分析中的应用[J].中国图象图形学报，2009，7(12)：1323-1328.

[6] 牛庆肖，张桦，徐光平.基于链码和快速傅里叶变换的轮廓描绘方法[J].光电子·激光，2013，24(6)：143-148.

[7] 张宇，刘文耀，邓伟.链码跟踪算法在三维医学图像处理中的应用[J].中国生物医学工程学报，2012，8(2)：256-261.

[8] 张瑞华，吴谨.基于优化水平集的细胞图像分割算法[J].电子技术应用，2013，30(16)：59-67.

[9] AWRANGJEB M.Robust image corner detection based on the chord-to-point distance accumulation technique[J].IEEE Transactions on Multimedia，2012，10(6)：109-114.