文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.08.015
中文引用格式： 刘稳健，蔡华杰，朱维杰. 基于参数识别的PMSM无位置传感器矢量控制[J].电子技术应用，2016，42(8)：67-69，73.
英文引用格式： Liu Wenjian，Cai Huajie，Zhu Weijie. Sensorless vector control of PMSM based on parameter identification[J].Application of Electronic Technique，2016，42(8)：67-69，73.
0 引言
随着永磁材料性能的不断提升和电力电子等技术的日益成熟，永磁同步电机（PMSM）由于其自身具有高效率、高转动惯量比、体积小等优势，在相关领域的应用越来越广泛[1]。
在PMSM矢量控制系统中，电机转子位置的检测是关键一环，只有精确获知转子的位置，整个系统才能平稳运行。现有的PMSM无位置传感器转子位置检测方法主要有：开环算法、观测器估计算法和高频注入法[2]。其中，滑模观测器因其具有性能优越、结构简单、鲁棒性好等优点，受到了相关领域的高度重视[5-8]。
本文设计了一种新型的位置估计算法，将滑模观测器（SMO）和电机参数辨识结合起来，利用改进的递推最小二乘法在线辨识电机参数，将辨识值反馈到SMO中，以达到提高转子位置检测精度的目的。
1 永磁同步电机数学模型
永磁同步电机是具有强耦合性的复杂模型，所以在研究中一般将其抽象为简单的数学模型，在dq坐标系下对PMSM建立数学模型如下。
电压方程：
磁链方程：
其中，ud、uq为d轴、q轴电压分量，Rs为定子电阻值， id、 iq为 d轴、 q轴电流分量，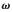
为转子角速度，
为定子磁链d轴、q轴分量，Ld、Lq为d轴、q轴电感分量。
2 遗忘因子递推最小二乘法在线辨识电机参数
最小二乘法是Karl Gauss于1795年提出的，他提出“未知量的最可能值是这样一个数据，它使各次实际观测值与计算值差的平方乘以度量其精度的数值以后所求得的和为最小”[9]。这一估计算法被广泛用于系统辨识和参数估计。最小二乘法的最大缺陷是系统要处理大量数据，所以要完成对电机参数在线辨识的目的有很大困难。为了改进该方法，在此基础上加入递推的思想：
新估算值
旧估算值
修正项
依据此概念可得出递推公式为：
上式中，
递推思想在定常的参数识别中比较常用，但是在PMSM矢量控制系统中，电机参数（定子电阻值和电感值）不是固定不变的。所以如果采用递推方法，由于数据不断积累，就会造成“数据饱和”现象。为解决该问题，本文引入遗忘因子概念。
目标函数为：
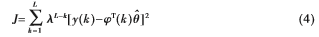
式中，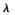
为遗忘因子，0<
<1。
由该目标函数可得出遗忘因子递推最小二乘法参数估计公式推导结果：
式中遗忘因子一般选择为：0.9<
<1。当
=1时，遗忘因子递推最小二乘法变成递推最小二乘法。
根据电机数学模型可得电机的状态方程：
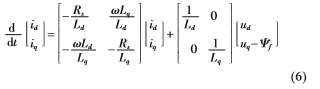
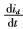离散化：
，T为辨识间隔时间，可得：
所以电机模型最小二乘法形式为：
由上式可知，电机参数定子电阻值Rs和电感值L均包含于等式右侧矩阵，所以理论上可以利用遗忘因子最小二乘法进行辨识，唯一的未知量是永磁体磁链
观察上式可知，永磁体磁链
只存在于iq中，在id中不存在。本文采用的是id=0的矢量控制策略，上式可以简化为：
利用遗忘因子递推最小二乘法对电机的两个参数进行在线辨识，令
则：
式中，
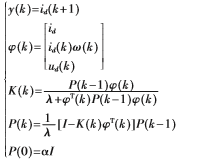
?琢取值范围是104～1010。先利用上式得出a和b的数值，再利用a(k)和b(k)方程求解出Rs和L，从而辨识出电机参数。
3 滑模观测器设计
滑模观测器源于滑模变结构，即利用切换函数强迫状态量沿滑模面运动，最终达到期望的状态位置。已知电机反电动势包含有转子位置和转速信息，根据电机数学模型构造如下滑模观测器[10]方程：
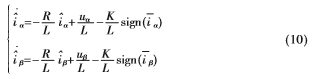
式中，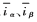
为
坐标系下的电流误差；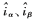
为电流观测值；K为常量增益。sign(x)为符号函数：
电流误差方程为：
利用Lyapunov稳定性准则函数保证滑模观测器稳定性，构造Lyapunov函数：
对上式求导数，并代入误差方程：
易知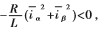
Lyapunov稳定性准则要求
，所以：
由此可得，欲使滑模观测器稳定可靠，则：K>
构造滑模面为：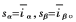
控制方法为函数切换控制：
u=ueq+Ksign(s(x))=e+Ksign(s(x))
系统进入滑动模态时，有：s(x)=0，
，经过有限时间间隔后
令电流估算方程中
得到
将在线辨识的定子电阻值和电感值反馈到滑模观测器中，不影响其鲁棒性，可改进SMO性能，减小电机参数变化带来的不利影响，有效提高转子位置估计精度，进而提高PMSM矢量控制系统整体性能。
4 仿真结果及其分析
仿真系统模型采用矢量控制，转速设定1 500 r/min，采用速度环和电流环双闭环控制。本文设计的控制系统电机参数为：额定功率550 W，额定电压220 V，定子电感8.5 mH，定子初始电阻2.875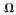 
，仿真时间设定为0.4 s。由于在实际工况中，电机定子电阻值和电感值基本不会在时间内有太大变化，所以不在同一次仿真中改变电机参数，通过与基于普通滑模观测器矢量控制系统对比，直接仿真验证电机参数变化后的系统性能。
4.1 基于普通滑模观测器矢量控制系统仿真分析
从图1可以看出，在电机定子电阻值达到3.25 
，而电感值减小到8 mH时，带普通滑模观测器的矢量控制系统电机实际转速波动较大，同时趋于稳定的时间增加，在大约t=0.15 s时才逐渐稳定，说明该滑模观测器的响应不够迅速。同时，估计转速对实际转速的跟随也不稳定。从图2可看出电机转子估计位置和实际位置有了较大误差，主要是由于电机参数变化后，滑模观测器参数没有相应变化。误差的累积严重时可导致系统崩溃，电机无法正常运行。说明在电机参数变化以后普通滑模观测器的性能下降，不能准确估计电机转子位置。本次仿真验证了基于普通滑模观测器的矢量控制系统在电机参数变化后系统整体性能下降明显，不能满足高精度控制要求。
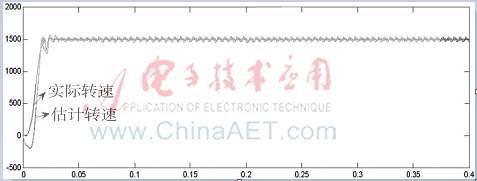
图1 基于普通滑模观测器矢量控制系统实际转速和估计转速对比
图2 基于普通滑模观测器矢量控制系统实际位置和估计位置对比
4.2 基于参数识别的PMSM矢量控制系统仿真分析
从图3可以看出，转速为1 500 r/min时，系统在0.08 s达到稳定状态，证明本系统具有优越的快速响应。估计转速在0.03 s以后实现对实际转速的快速响应。但是在转速较低时转速明显波动较大，这也是滑模观测器存在的问题，即在电机低速时的性能并不理想，主要是由于反电动势的值太小。由图4可以看出，在大约t=0.07 s时，转子估计位置与实际位置基本完全重合，主要是由于改进后的滑模观测器参数能够随电机参数的变化而相应变化。说明了本系统位置估计的精确性很高，同时响应迅速。在t=0.07 s之前，转速没有达到1 500 r/min时，转子位置估计误差很大，这是滑模变结构自身抖振问题引起的误差，但是在转速稳定后估计误差几乎为0，间接说明滑模观测器在高速时的优越性。本次仿真验证了基于参数识别的PMSM矢量控制系统能够很好地克服电机参数变化带来的不良影响，整体性能表现优越。
图3 基于参数识别的PMSM矢量控制系统实际转速和估计转速对比
图4 基于参数识别的PMSM矢量控制系统转子实际位置和估计位置对比
5 结论
本文创新性地将遗忘因子递推最小二乘法在线辨识电机参数和滑模观测器结合起来，很大程度上减小了在电机运行过程中参数变化对滑模观测器性能的影响。本文设计的改进型滑模观测器在估计转子位置时具有良好的性能表现，同时在很大程度上提高了系统的整体性能。
参考文献
[1] 王松.永磁同步电机的参数辨识与控制策略研究[D].北京：北京交通大学，2011.
[2] KANG J，HU B，LIU H，et al.Sensorless control of permanent magnet synchronous motor based on extended kalman filter[C].In：Preceeding of the International Conference on Services Science，Managent and Engineering，2009，567-570.
[3] WU G，XIAO X.Speed controller of servo system based on mras method[M].Gippsland，VIC.2009：1-5.
[4] YU C S，KAI S，HONG Y M.Permanet fiux identification of PMSM based on EKF with speed sensorless control[M].Glen dale，AZ.2010：2252-2257.
[5] ORLOWSKA K T，DYBKOWSKI M.Stator-current-based mras estimator for a wide range speed-sensorless induction-motor drive[J].Industrial Electronics，IEEE Trans.2010，57(4)：1296-1380.
[6] LIU S M，DING L J.Application of adaptive fuzzy sliding mode controller in pmsm servo system[C].In：Preceedings of the International Conference on Computing.Control and Industrial Engineering(CCIE)，2010，2：95-98.
[7] WANG Y H，ZHANG X Z，YUANG X F.Position-sensorless hybrid sliding-mode control of electric vehicles with brushless dc motor[J].IEEE Transactions on Vehicular Technology.2011，60(2)：421-432.
[8] FENG Y，ZHENG J，YU X H.Hybrid terminal sildingmode observer design method for a permanent-magnet synchronous motor control system[J].IEEE Transactions on Industrial Electronics.2009，56(9)：3424-3431.
[9] 庞中华，崔红.系统辨识与自适应控制MATLAB仿真[M].北京：北京航空航天大学出版社，2009.
[10] Hongryel Kim，Jubum Son，Jangmyung Lee.A hign-speed sliding-mode observer for the sensorless speed control of a PMSM[J].IEEE Trans.on IE，2011，58(9)：4069-4077.