张宝荣1,2,金森林1
(1. 燕山大学 信息科学与工程学院, 河北 秦皇岛 066004;2. 河北省特种光纤与光纤传感重点实验室, 河北 秦皇岛 066004)
摘要:提出了一种利用压缩感知原理测量微弱信号的方法,测量信号由伪随机序列调制,应用改造的测量矩阵,在一次测量基础上进行二次测量,利用压缩感知的恢复算法可以精确地确定信号在字典中的位置并且得到其幅度值。仿真实验证明本文方法可以用于检测信噪比高于-20 dB的微弱信号,将信号较完整地从噪声干扰中恢复出来,信号幅度误差很小。
中图分类号:TN911.72文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.08.024
引用格式:张宝荣,金森林.基于压缩感知的微弱信号检测方法[J].微型机与应用,2017,36(8):76-78,82.
0引言
随着现代信息技术的迅猛发展,人们不仅对信息量的要求剧增,而且对信息准确度的要求也越来越高。在信号测量过程中,信号经常会被湮没在测量系统的噪声和干扰中,如何准确地测量这些微弱信号是一个亟需解决的问题。

图1压缩感知微弱信号测量系统由于信号、噪声和干扰的特点不同,检测方法也迥异。目前,微弱信号的检测技术[12]主要有三种:(1) 相干检测与频域窄带化技术,利用噪声与信号符合同频又同相的可能性很小的特性检测微弱信号,锁相放大器是这种方法的典型[3];(2) 时域信号的积累平均法,基于信号的稳定性和噪声的随机性,由于信号周期性地重复,噪声却不具有这个特性,因此只要重复的次数足够多,就可以把噪声中的微弱信号提取出来,而且重复的次数越多,提取微弱信号的能力越强[4];(3) 新兴的利用混沌理论和小波技术来检测微弱信号[57]。
2006年,DONOHO L、CZNDS J和TAO T等人提出了压缩感知(Compressive Sensing)理论[89],这是一种全新的信号获取和处理理论。压缩感知理论认为只要信号在某已知变换域具有稀疏性,就可以通过原信号在某投影域的投影近似无损地重构原始信号,只要求投影域的基与已知变换域的基是不相干的。利用压缩感知方法不仅可以对信号进行采样和压缩,而且能够去除微弱信号噪声,更加精确地实现了原始信号的恢复和重构。
本文在传统微弱信号去噪方法的基础上,基于压缩感知的思想,将微弱信号与改进的测量矩阵做相关,得到相关系数,然后通过OMP算法[10]将微弱信号重构。
1应用压缩感知检测微弱信号原理
为了测量系统的某些特性,把已知信号输入到待测系统中,系统会影响信号的某些参数,测量输出信号,比较输出与输入信号的差异,可以得到系统的特性。在信号通过系统时,系统内的噪声和系统外的干扰都会叠加到输出信号中,降低了输出信号的信噪比,增大了测量误差。如何在低信噪比条件下准确地测量信号是关键问题,因此设计了应用压缩感知原理测量微弱信号的测量系统,见图1。
测量所用输入信号是正交字典稀疏表示的信号x,设正交字典为Ψ,其稀疏表示为θ,即x=Ψθ。输入信号x通过待测量的系统后的输出信号x′=Ax+n,其中n表示测量过程中叠加的噪声和干扰,A是待测系统的增益。压缩感知的测量过程是利用测量矩阵Φ来获取信号的信息,测量结果为y=Φx,信号的重构依据求解最优化问题minθ0s.t. y=ΦΨθ。如果选择合适的输入信号x和测量矩阵Φ,通过两次测量的方法就可以将输出信号中的噪声和干扰去除,得到高信噪比的信号Ax。
1.1信号与正交字典的选取
本文选取了伪随机序列中的m序列 [11]作为测量原始信号。正交字典是一组正交基,任意信号都可以用正交字典来表示,若其表示中仅有几项不为零, 则称为信号的稀疏表示。根据m序列的性质,m序列的循环移位仍然是m序列,再根据m序列的自相关和互相关特性,m序列及其N-1个循环移位序列可以组成一个正交字典。即:
Ψ=(m,m1,m2…,mN-1)T
其中mi,i=1,2,…,N-1表示m序列的循环移位序列,i是位移数。
1.2测量矩阵
测量矩阵Φ有多种选择,只要满足RIP条件[12]即可,其中随机高斯矩阵是最常见的一种。测量矩阵Φ的行数m与信号的稀疏程度k有关,m应该满足m≥klog2(N/k)。
由于被检测信号是微弱信号,信噪比低,当测量矩阵为高斯矩阵时,不能够保证高概率地从随机投影获得的少量测量值中将特征量准确地提取出来。因此,测量矩阵Φ需要改造,将高斯矩阵中的任一行替换为原始信号,不失一般性,可以选取第一行。为了使测量矩阵Φ满足RIP条件,替换信号kx,必须满足k1,测量矩阵Φ成为以下结构:
Φ=(kx,g2,g3…,gm)T
其中gi,i=2,3,…,m是随机高斯矩阵的各行。
1.3信号处理方法
为了从噪声中恢复信号,采用的信号处理方法是,首先应用OMP算法从测量信号y1=Φ1x′中恢复含噪声的信号x′的稀疏表示θ1,根据OPM算法的特性得到的θ1应该是以下形式:
θ1=(kA,…,θi,…,θj,…0)T
其中kA为信号的稀疏表示系数,θi,θj表示噪声不为零的稀疏表示系数。所以含噪声的信号的第一次信号恢复结果为:x1=kAx+∑m=i,j,…mθmgm。求和项表示噪声中与测量高斯矩阵最相似的那些向量。
为了除去噪声,重新选取随机高斯矩阵Φ,替换第一行后形成新的测量矩阵Φ2,对第一次恢复信号x1再进行测量,y2=Φ2x1。对测量结果y2应用OPM算法再次进行恢复稀疏表示θ2,则:
θ2=(k2A,…,0)T
除去第一项其他项都为零,原因是新选取的高斯矩阵与原高斯矩阵相同的概率极小,即一次恢复信号x1中的噪声既然与一次测量的高斯矩阵中的某些向量相似,则不可能与二次测量矩阵中的向量相似,所以稀疏表示的系数都是零。
恢复后的信号为x2=k2Ax,已经除去了噪声和干扰,k为已知,因此可以得到去噪的信号Ax。
2仿真与实验
为了验证上述理论分析,首先进行了仿真,线性反馈移位寄存器是产生m序列的最简便的方法,n位移位寄存器产生长度为2n-1的m序列。本文选取由10位移位寄存器产生的长度为1 023的m序列,反馈系数为0,0,1,0,0,0,0,0,0,1。序列如图2所示。

当被测信号通过检测系统时,检测系统中的噪声会加到信号上,本文选用的是加性高斯噪声,即含噪信号为x′=aamx+nam。共中aam是信号的幅值,nam为高斯噪声的幅值。通过调整aam,nam的大小,可以得到不同信噪比的含噪信号如图3所示。

根据上节的方法,采用的是OMP算法进行信号的恢复,α=0.001,不同信噪比的信号恢复结果如图4所示。在信噪比分别为-10 dB和-20 dB时,第一次测量所得到的特征量的位置由于噪声的干扰,随噪声的增大而不准确。而在进行第二次测量后,噪声特征量由于两次测量的测量矩阵是随机产生的,使得噪声特征量的重合概率几乎为0,但是信号特征量的位置依然不变,因此可以在第图4二次测量后的信号恢复二次测量后准确地找到信号特征量的位置,并获取其幅值。

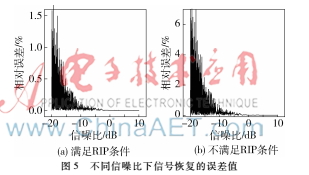
图4中信号的幅值还存在一定的误差,当信噪比为-10 dB和-20 dB时,测量矩阵在不满足RIP条件下和满足RIP条件[13]下恢复信号的误差如图5所示。由图5可知,在满足RIP条件的情况下,对于信噪比为-20 dB的含噪声信号,通过OMP算法,能够准确地找到特征量的位置,恢复信号的幅度误差较小,而测量矩阵不满足RIP条件的情况下,恢复信号误差较大,当信噪比再降低时,不能够准确地找到特征量的位置。
利用LabVIEW构建了实验系统,噪声是电阻的热噪声,m序列由虚拟仪器产生,控制信号幅度,二者相加可以得到不同信噪比的被测信号,如图6所示。
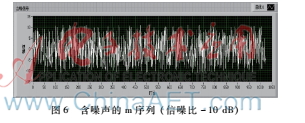
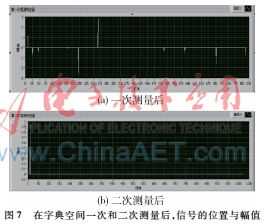
图6含噪声的m序列 (信噪比-10 dB)LabVIEW系统采集被测信号,应用OMP算法进行信号恢复,结果如图7所示,与仿真结果是一致的。对不同信噪比的信号进行了多次实验,信号的恢复误差见表1,随着信噪比的降低,恢复信号的误差增大,当信噪比低于-25 dB后,恢复信号的误差剧增,本文的方法已经不适用。

3结论
本文简要介绍了一种新的检测微弱信号的方法,基于压缩感知原理,根据噪声和信号本身具有的特性,通过改造测量矩阵和在原有的测量基础上再进行一次测量,由重构算法找到特征量的位置并测出其幅值的大小,进而将原始信号恢复出来。通过仿真和实验证实,在信噪比不低于-20 dB的情况下,重构信号误差较小,若在测量矩阵的选取和信号的处理方法上再做进一步的改进,有望在更低的信噪比条件下更精确地恢复信号。
参考文献
[1] 陈佳圭. 微弱信号检测[M]. 北京:中央广播电视大学出版社, 1987.
[2] 夏均忠, 刘远宏, 冷永刚,等. 微弱信号检测方法的现状分析[J]. 噪声与振动控制, 2011,31(3):156-161.
[3] 朱虹,林君,吴忠杰,等. 近红外光谱仪中的数字锁相技术研究[J]. 仪器仪表学报,2006,27(10): 1258-1261.
[4] 王玉田,监雄,王惠新,等. 基于Boxcar滤波器的荧光检测二氧化硫信号的去噪研究[J]. 光谱学与光谱分析, 2012,32(12):3285-3289.
[5] Xu Yanchun, Yang Chunling, Qu Xiaodong. A new approach to detecting weak signal in strong noise based on chaos system control[J]. Chinese Physics B, 2010, 19(3): 202-206.
[6] 范剑,赵文礼,王万强. 基于Duffing振子的微弱周期信号混沌检测性能研究[J].物理学报, 2013,62(18):180502.

