文献标识码: A
DOI:10.16157/j.issn.0258-7998.172513
中文引用格式: 字然,常俊,宗容,等. 基于改进空间插值的无线电环境地图生成技术[J].电子技术应用,2018,44(3):103-107.
英文引用格式: Zi Ran,Chang Jun,Zong Rong,et al. Research on the construction of radio environment map based on revised spatial interpolation[J]. Application of Electronic Technique,2018,44(3):103-107.
0 引言
近年来,推行动态频谱管理已成为国际主流趋势。认知无线电(Cognitive Radio,CR)的提出打破了传统封闭式、保护式的频率划分机制,允许无线通信设备及系统对周围频谱环境进行动态感知,并以高效、灵活的方式进行频谱接入[1]。为进一步改善认知无线电系统性能,无线电环境地图(Radio Environment Map,REM)技术应运而生。
REM是对复杂无线电环境的一种数字化抽象,反映多维无线电环境及场景信息,其概念最早由学者赵友平于2005年提出[2],现已得到创新无线国际论坛(Wireless Innovation Forum)的认同以及IEEE、ITU-R、ETSI相关标准文件的采纳或引用[3]。2010年,欧盟第七框架计划(Framework Program 7,FP7)启动研究项目FARAMIR(Flexible and Spectrum-Aware Radio Access through Measurements and Modelling in Cognitive Radio Systems),其核心任务就是开发一套完整的REM原型系统,增强欧洲工业在无线频谱优化、无线电监管方面的创新能力[4-7]。目前,多个大学、研究机构对基于REM的频谱管理技术做了研究[8-12]。
空间插值(Spatial Interpolation)是一种利用已知数据点来估计其他未知节点,从而填补数据点之间的空白的方法[13],广泛应用于地理信息系统(GIS)、图像处理及室内定位等领域。常用的空间插值算法有反距离加权(Inverse Distance Weighting,IDW)法[14-15]、自然邻域法[13]、样条函数插值法[16]及克里金插值法[17]等。本文对空间插值算法进行比较、改进,将空间插值算法应用于无线电环境分析,提出一种基于接收信号强度(RSS)以及空间插值的REM生成方法。
1 空间插值
1.1 通用模型及经典算法
空间相似性是空间插值的基本原理,即越接近数据点的值,与数据点相似程度越大。空间插值的通用模型为:

其中,P(x0,y0)为待插值点(x0,y0)某属性的估计值,P(xi,yi)为N个已知数据点在各个位置(xi,yi)上的属性值,ωi(x0,y0)为各数据点对待插值点分配的权值。
经典IDW算法是一种全局空间插值算法,最早由SHEPARD D提出[14]。该方法将已知数据点对待插值点的权值ωi视为距离的负幂指数。该方法实现简单,提出后被广泛应用。
由RENKA R J提出的优化型Shepard算法(Modified Shepard′s Method,MSM)[15]对经典IDW算法进行了较大改进。为提高计算效率,MSM算法定义待插值点的影响半径R,只考虑di≤R范围内数据点对待插值点的影响,从而将权值ωi计算式定义为:

其中,di为待插值点(x0,y0)与某一数据点(xi,yi)之间的欧式距离,dexp为权重指数。该算法的理想模型为所有数据点在区域中按正方形网格均匀分布。
1.2 改进型MSM算法
本文在MSM算法基础上,提出一种改进型MSM算法(Revised Modified Shepard′s Method,RMSM),从以下3个方面进行改进:
(1)进一步优化权值计算。由于REM应用场景中,数据点分布不一定为理想模型。当数据点少、分布不均时,MSM算法将会出现权值ωi分配不合理的情况。因此,RMSM算法将权值ωi定义为一个相对值:

其中,i=1,2,…,N;ω0为距离待插值点最近点的权值,ωi仍利用式(2)计算。
(2)灵活地使用局部特征。MSM算法提出了将数据点拟合为节点方程Q(x,y)的思想,其目的是利用某一数据点(xi,yi)影响半径R内其他数据点的局部特性,对其自身RSS值P(xi,yi)进行优化调整。但在实际REM场景下,影响半径R的选取存在一定局限性,如:当数据点分布不均(如集中于某一点附近)时,MSM算法可能会出现影响半径R内数据点较少甚至无数据点的情况。为此,RMSM算法通过选取NW个近邻节点进行待插值点RSS值的估计,并选取Nq个近邻数据点来对这NW个点进行节点方程Q(x,y)的拟合。
区域中某一数据点(xk,yk)的节点方程Qk(x,y)可为多种形式,而为了更贴近REM场景下无线电传播特性,RMSM算法采用式(4)所示的二次形式来拟合:
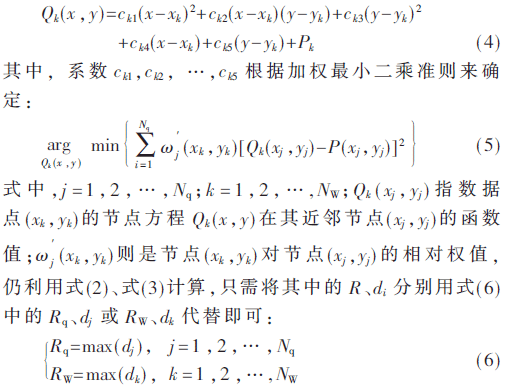
式中,1<Nq,NW≤N;dj为区域中某一已知数据点(xi,yi)与选取的Nq个数据点中某一数据点(xj,yj)的欧式距离;dk为待插值点(x,y)与选取的NW个数据点中某一数据点(xk,yk)的欧式距离,如图1所示。Nq、NW无必然联系,可以相等,也可不等。
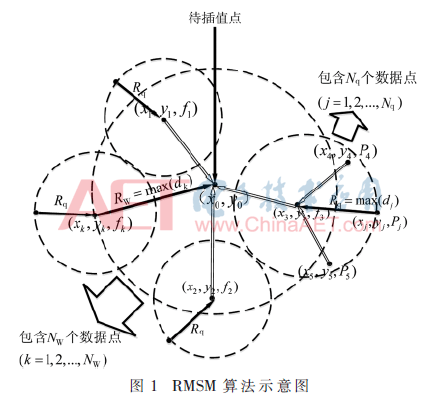
(3)高效的近邻搜索法。为了找到待插值点(x0,y0)的NW个近邻节点以及其中每一个点的Nq个近邻节点,RMSM算法通过构造KD-Tree数据结构来进行两次近邻搜索。KD-Tree(k-Dimensional Tree)数据结构[18]通常用于k维空间中的范围搜索及近邻搜索。KD-Tree通过超平面分割空间,将空间中的数据点划分为一种特殊的二叉树结构,在进行近邻搜索时只用通过其子树回溯查找,无需遍历所有数据点,当数据点多时可大大减少搜索次数。搜索结束后,将选取的NW个数据点RSS值优化为:

理想的空间插值是将离散的数据点扩展为连续的数据曲面,而实际中为了将点数据尽可能扩充为面数据,常利用网格化的思想,即将插值区域按一定的分辨率(即网格大小)划分为网格区域,并对每一个网格点进行空间插值。无线电环境地图(REM)的生成就是将若干个位置的RSS扩展为区域性的综合信号强度,利用已知数据点进行网格化插值。
2 算法流程及复杂度分析
2.1 算法主要流程
(1)输入:
①RMSM算法相关参数:N、dexp、Nq、NW。
②网格区域相关参数:Xmin、Xmax、Ymin、Ymax,网格点数M=Xpoints×Ypoints。(Xpoints、Ypoints为两个坐标轴上的网格点数)
(2)初始化:
①数据点矩阵points:
double[,] points=new double[N,3]
并输入数据:

②权值矩阵ω′与节点方程值矩阵q:
double[] w1=new double[Nq]
double[] w2=new double[Nw]
double[] q=new double[Nw]
③网格点(即所有待插值点)矩阵XY:
double[,] XY=new double[xPoints,yPoints]
(3)将points中的数据集构造为二维KD-Tree数据结构;
(4)从第一个网格点(m=1)开始,重复以下步骤①~③:
①搜索待插值点的NW个近邻数据点,利用式(4)计算权值,从而:

②分别搜索NW个数据点的Nq个近邻数据点,利用式(6)进行节点方程拟合,输出节点方程值矩阵q:

③输出结果:

(5)直至最后一个网格点(m=M)计算完毕,输出M个结果,算法结束。
2.2 复杂度分析
IDW Classic算法是一种全局插值法,利用空间中所有数据点进行插值,当数据点为N时,其复杂度为O(N);当空间中网格点数为M时,利用该算法生成无线电环境地图(REM)复杂度将达到O(MN)。MSM与RMSM均为局部插值法,一般情况局部数据点数N′<N(取决于影响半径R及参数Nq/NW的选取),两种算法都使用复杂度为O(logN)的近邻(NN)搜索法寻找局部数据点,因此总体复杂度均为O(MlogN)。
不难看出,MSM及RMSM算法较IDW Classic在计算效率上已明显提高,而选取的网格越密,则REM越接近连续的数据面,但带来的计算量也越大。
3 实验及分析
3.1 实验场景
本实验在一个15 m×20 m的室内区域进行,存在一定的墙、障碍物等非视距传播环境,总体传播环境良好。区域内均匀分布6个路由器(图2中TX1~TX6)发射2.4 GHz WiFi信号,用手机测量其信号强度(RSS)。

本文的算法均在Visual Studio 2010开发平台下利用C#实现,并使用SQL Server 2008数据库存储相关数据。首先,利用6个路由器随机组合6种不同的无线电场景,每个场景测量50个不同位置的信号强度(RSS,单位为dBm)。之后,使用前文所述的算法进行实验,每个场景选择3个点(图2中误差分析点P1~P3)来计算插值(即每个点计算3×6=18次)。实验相关参数设置见表1。

3.2 误差分析
图3展示了3种算法(IDW Classic、MSM及RMSM)在不同数据点N下的误差棒图,图中柱状图表示该算法的平均绝对误差(MAE):

式中,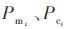 分别为RSS测量值与计算值,S为实验次数(此处S=18)。线段的长度表示误差的标准差,关于平均误差值对称,其大小反映了一个算法的稳定性。
分别为RSS测量值与计算值,S为实验次数(此处S=18)。线段的长度表示误差的标准差,关于平均误差值对称,其大小反映了一个算法的稳定性。
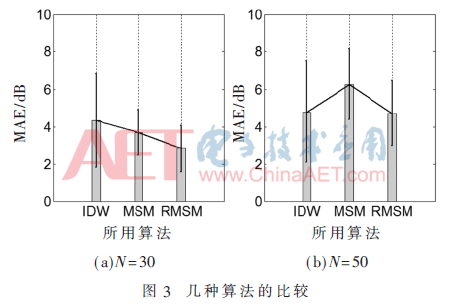
IDW Classic算法由于使用所有数据点进行计算,复杂度较高,加之测量数据本身具有一定误差,其稳定性不如其他算法(标准差大),平均绝对误差(MAE)也较大;MSM算法虽然稳定性优于IDW Classic,但在数据点较少时性能最差,如图3(a)所示;而由于RMSM算法优化了权值分配并灵活地选择数据点,与IDW Classic算法相比,图3中可明显看出稳定性提高了近一半(N=30、N=50时分别提高了50.4%、55.37%),在数据点较低时也能保持较低的MAE及良好的稳定性。
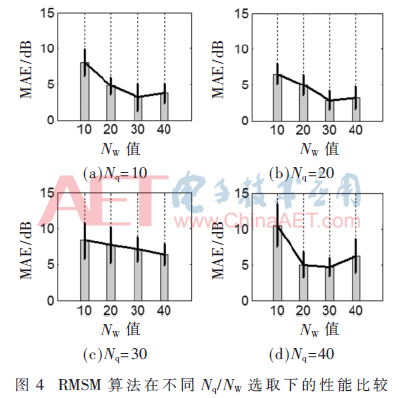
图4展示了RMSM算法在不同Nq/NW选取下的情况。由于室内传播环境良好,因此Nq=20时算法性能较好,如图4(b)所示,最佳情况为Nq=20,NW=30,此时MAE≈2.85 dB(与IDW Classic相比降低了1.96 dB),算法稳定性也良好,标准差在2.48 dB左右。若传播环境较差(存在较多非视距传播情况),则需选取较大Nq、NW值进行实验。
3.3 无线电环境地图(REM)的生成
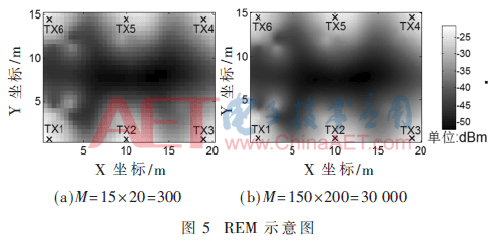
基于以上分析,本实验采用各方面性能较为良好的RMSM算法。实验场景仍为图2所示场景,6个路由器(TX1~TX6)同时工作。随机选取50个位置测量信号强度RSS(即数据点N=50)其中设置参数Nq=20,NW=30。图5展示了不同网格点数M下生成的REM示意图,图5(a)网格点数M=1 200,图5(b)M=30 000,可见,离发射机越近的位置信号强度(RSS)越大;另外,M越大,REM越接近于连续的数据曲面。
4 结论
本文在国内外认知无线电(CR)、无线电环境地图(REM)领域相关文献的研读及FARAMIR项目技术报告的学习基础上,介绍了空间插值的一般模型,提出了一种基于接收信号强度(RSS)及空间插值的REM生成技术,为当前及未来的动态频谱管理提供了灵活的手段及一定的信息支撑。文章通过误差分析比较了各个算法的性能,实验表明,RMSM空间插值算法具有计算效率高、误差较小、稳定性好等优点,可用于REM的生成。未来将考虑结合无线电传播模型的自适应Nq/NW算法以及基于REM的指纹库构建研究。
参考文献
[1] 黄标,李景春,谭海峰,等.认知无线电及频谱管理[M].北京:人民邮电出版社,2014.
[2] ZHAO Y P,REED J.Network support:The radio environment map[M].Cognitive Radio Technology-Bruce Fette(Ed.1).Ch 11,Elsevier 2006:337-339.
[3] 赵友平,谭琨,姚远.认知软件无线电系统原理与实验[M].北京:清华大学出版社,2016.
[4] Deliverable D2.4:Final System Architecture.EC FP7-248351 FARAMIR project[R].2011:8-10.
[5] Deliverable D4.1:Final System Architecture.EC FP7-248351 FARAMIR project[R].2011:8-12.
[6] Deliverable D4.3:Final System Architecture.EC FP7-248351 FARAMIR project[R].2012:7-15.
[7] Deliverable D6.2:Final System Architecture.EC FP7-248351 FARAMIR project[R].2011:10-22.
[8] 王岭.WRAN中无线电环境地图的生成技术研究[D].重庆:重庆大学,2011.
[9] 李晔.基于高铁频谱环境地图的切换技术研究[D].成都:西南交通大学,2013.
[10] 李伟,冯岩,熊能,等.基于无线电环境地图的频谱共享网络研究[J].电视技术,2016,40(10):60-66.
[11] Luo Yuan,Gao Lin,Huang Jianwei.Economics of data-base-assisted spectrum sharing[M].Wireless Networks,2016.
[12] 高远,周文虎,匡正.无线电环境地图技术实现与前景[J].上海信息化,2015(11):66-67.
[13] 张梦洁.结合GIS的室外WiFi信号覆盖强度分析研究[D].汕头:汕头大学,2012.
[14] SHEPARD D.A two dimensional interpolation function for irregularly spaced data[C].In proc.of the 23rd National Conf.of the Association for Computing Machinery,Princeton,NJ,ACM,1968:517-524.
[15] RENKA R J.Multivariate interpolation of large sets of scattered data[J].ACM Transactions on Mathematical.Software,1988,14(2):139-148.
[16] 陈岭,许晓龙,杨清,等.基于三次样条插值的无线信号强度衰减模型[J].浙江大学学报(工学版),2011,45(9):1521-1527.
[17] 刘志建,关维国,华海亮.基于克里金空间插值的位置指纹库建立算法[J].计算机应用研究,2016,33(10):3139-3142.
[18] BENTLEY J L,FRIEDMAN J H.Data structures for range searching[J].ACM Computing Surveys,1979,11(4):397-409.
作者信息:
字 然,常 俊,宗 容,王若男,廖贵文
(云南大学 信息学院,云南 昆明650500)

