0 引言

    图像边缘检测是数字图像处理领域中的一项关键技术^[1-3]，广泛运用在军事、农业、工业、医学、航天等领域^[4-6]。随着电子信息技术的快速发展，各大相关领域对图像边缘检测技术提出更高的要求，即：在保证精度的前提下，即时处理大规模数据。

    文献[6]、[7]使用硬件并行技术和流水线技术,大幅增加了数据的吞吐量，但在计算Sobel的梯度值时速度较慢,限制了系统的整体处理速度^[6-7]。文献[8]在文献[6]、[7]的基础上，解决了Sobel梯度值计算速度较慢的问题，使系统的整体处理速度提升^[6-8]，但该方法牺牲了精度，导致边缘检测的效果较差。

    针对上述问题，本文采用优化的CORDIC算法，将Sobel梯度计算公式转换成数据的移位和相加的流水线操作，在保证运算精确度的前提下，大幅提高整体运算速度。

1 Sobel边缘检测算法

    Sobel算子是一阶导数的边缘检测算子，具有2组3×3的矩阵。图像中的像素点分别和这两个矩阵做卷积后，即可得到图像的水平、垂直梯度。根据式(1)和式(2)得到图像梯度值后，将该值和预设的阈值进行比较，即可判断该点是不是图像的边缘部分。

    图1(a)为待处理的图像数据，图1(b)、图1(c)为用于计算x和y方向梯度值的卷积表。

    水平梯度P_x、垂直梯度P_y的计算公式如式(1)所示：

    式(1)可以利用两个行缓冲器(Line_buffer)和流水线型的乘加器完成。如图2所示，当预存满两个行缓冲器后，再等2个时钟，系统即可实时地得到待处理的图像数据。

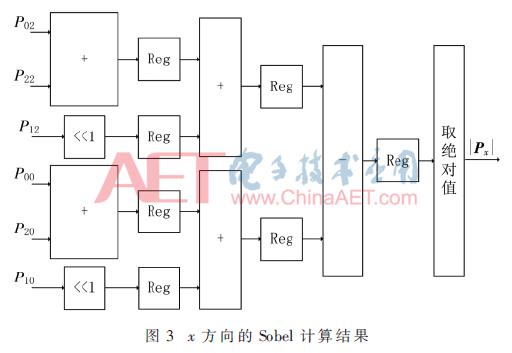
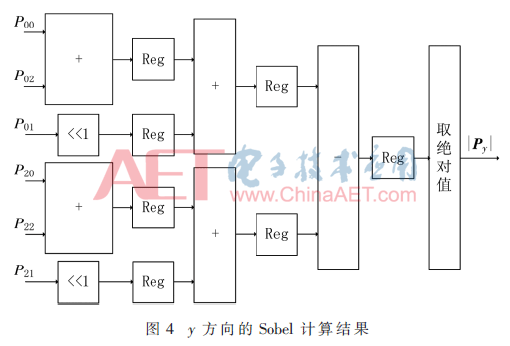
    如图3所示，得到待处理的图像数据后，P₀₂和P₂₂直接进行加法运算，P₁₂通过移位操作实现乘2效果。为降低D触发器(Reg)之间的逻辑时延，增加系统的工作频率，本文将P₀₂和P₂₂相加的结果、P₁₂移位的结果寄存了一拍后，再进行加法运算。依据上述原理，对P₀₂、P₂₀和P₁₀进行了类似操作。最后将两组数据做减法，再取一个绝对值即可得到x方向的Sobel计算结果。y方向的Sobel计算方法如图4所示，与图3的原理类似。

    最终梯度值可以根据梯度计算公式算出：

    依据式(2)，即可得到最终梯度的模值|G|，将梯度的模值和阈值进行比较，就可以判断出该点是否为边缘点。关于梯度模值计算公式，文献[6]和文献[7]选择调用IP核实现平方根运算，该方法在一定程度上保证了计算精度，但是运算速度受限。文献[8]为解决这个问题，选择将式(2)等效为|G|=|P_x|+|P_y|，较好地提高了运算速度，但是运算精度大幅度降低。

    为解决上述问题，本文选择用优化的流水线型的CORDIC算法，实现式(2)的运算。该方法既保证了精度，又提高了运算速度。

2 CORDIC算法原理

2.1 圆周系统下的CORDIC算法

    为在保证运算精度的前提下，提高Sobel 算法的即时处理速度和数据吞吐量，本文选择使用CORDIC算法对其进行优化。CORDIC是将复杂的计算转换成移位和加法的迭代操作。CORDIC算法有旋转模式和向量模式。在不同的坐标系下使用，可以实现不同的功能。因需要实现式(2)，本文选用圆周坐标系下的向量模式。

2.2 向量模式

    向量模式下通过一系列的角度逼近，可以进行反正切和平方根的计算。旋转模式的完整迭代公式如式(3)所示。其中x_i为当前的横坐标值，y_i为当前的纵坐标值，z_i为当前的角度累加值。其中y_i控制着判决算子δ_i的值，y_i的值为正时，δ_i为负；y_i的值为负时，δ_i为正。

3 向量模式下CORDIC算法的优化

    为提高系统的总体性能，本文对CORDIC算法进行了一定优化，最终提高了CORDIC算法的精度和速度。

3.1 覆盖角度的扩展

    如式(6)所示，CORDIC算法的旋转角度有固定的规律，角度为2^-i的反正切。当迭代次数趋于无穷时，所有角度值之和约等于99.827°。由此可知，覆盖角的度数为[-99.827°，99.827°]，不能覆盖圆周上的所有角度。

    考虑到只需求解式(2)，输入数据的符号变化不影响最终计算结果。因此在式(1)处，直接求取了|P_x|、|P_y|，通过该操作将所有数据计算限制在了第一象限。为减少迭代次数，还可将输入数据进行进一步的处理。将|P_x|和|P_y|进行比较，如果|P_y|大于|P_x|，则将|P_y|和|P_x|的值互换；如果|P_x|的值大于|P_y|，则|P_y|和|P_x|的值保持不变。预处理后，数据的象限限制在[0°，45°]。因此可以减少一级迭代，收敛域也因此变为[-57.827°，54.827°]。经过上述处理后，式(5)变化成式(7)。

3.2 数据位扩展

    CORDIC算法的迭代次数和运算数据的位宽对运算结果的精度有很大的影响。YU Y H在文献[9]中提出了解决量化误差(OQE)的方法。

    YU Y H指出OQE由近似误差和舍入误差组成。近似误差是由有限个确定旋转角度量化CORDIC旋转角度带来的量化误差，由最大向量模值和迭代次数决定。舍入误差是因为计算时数据位不够带来的误差，由数据的位宽决定。

    增加数据位宽和迭代的次数都可以提高运算结果的精度。但是，当迭代次数达到一定值后，迭代次数的增加对运算精度的影响变得很小。而增加运算数据的位宽将带来较好的效果，大幅度降低舍入误差。每增加一位数据位宽，舍入误差将变小1/2^[9]。本文在用CORDIC算法实现式(2)时，在保证较大的迭代次数的前提下，将运算数据位扩展3位，大幅度降低了舍入误差。

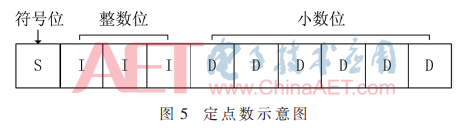
    在进行数据迭代运算时，考虑到采用浮点数可以降低工作频率，因此采用了定点数。如图5所示，定点数由符号位(S)、整数位(I)、小数位(D)构成。

3.3 优化后CORDIC算法的实现

    圆周模式下的向量模式可以根据输入的|P_x|和|P_y|，直接求解出最终梯度的模值。梯度模值运算模块的硬件结构图如图6所示，由预处理、CORDIC迭代流水线、后级处理3部分组成。预处理部分中，将判断|P_x|和|P_y|的值是否需要互换。因为迭代次数已经提前确定，缩放因子已知，在预处理阶段的数值修正部分可以提前对最终结果进行补偿。补偿后，将数据位数从24位扩展成27位。扩展后，舍入误差将降低为之前的1/8，提高了运算的精确度。

    预处理后进入CORDIC迭代部分，迭代部分采用15级的流水线模式。根据式(3)可知，在求解式(2)时只需要知道|P_x|和|P_y|的值，因此可舍弃z_i的计算，以此节约一些资源。如图7所示，迭代部分的每行存在两个移位寄存器和两个加/减法器。符号控制信号为Sign，由y_i决定。通过式(3)可知，当y_i为正时，x_i处选用加法器，y_i处选用减法器；当y_i为负时，x_i处选用减法器，y_i处选用加法器。

    数据通过迭代部分后，进入后级处理部分。后级处理部分将信号缓存一拍后，进行截位处理，然后就可得到x₁₅[26:3]的值，即最终梯度的模值。此外，该设计采用了流水线结构，提高了吞吐量和最大工作频率。

4 系统仿真及性能分析

    本设计在ISE14.7软件下，用Verilog HDL语言进行了实现。此外，使用MATLAB、Modelsim SE 10.1c进行了本设计的测试。

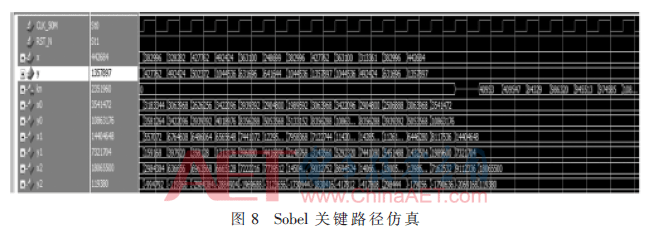
    本文在Xilinx ISE编译器中编译好代码后，通过Modelsim进行了软件仿真。图8为本设计关键路径的仿真：CORDIC迭代运算的仿真。修正后的|P_x|和|P_y|采用定点数的方法进行表示，总计24位，0～12位为小数位，13～22位为整数位，23位为符号位。|P_x[26:0]|和|P_y[26:0]|为|P_x|、|P_y|扩展3位后的值，分别用x、y进行表示。K_n为最终梯度模值的计算结果。为了更直观地表示，输入值、中间值和输出结果均用有符号十进制数进行表示。根据仿真结果可知，采用优化后的CORDIC进行式(2)的运算，精确度约为10^-4，远大于文献[8]的精确度。

    仿真后，将文献[8]的算法和本文的算法进行了对比测试，结果如图9所示。通过图9(b)可以观察到，使用文献[8]的加速算法后，因为精确度较低的缘故，不能较好地检测到边缘，人像左下方、右上方处的头发边缘和背景混杂在了一起，人像面部左下方、右上方的边缘检测效果较差。使用本文的改进算法后，如图9(c)所示，在保证运算速度的前提下，较好地识别出了图像的边缘，较好地检测出了头发和面部的边缘，与图9(d)使用MATLAB实现Sobel算法的效果近似。

    本文也尝试使用Xilinx ISE自带的平方根IP核实现关键路径的计算。选用Spartan6 XC6SLX16 2CSG324C芯片在Xilinx ISE14.7软件平台下，对平方根IP核进行编译综合。编译综合后，得到ISE计算出的最高工作频率信息。为测试本文使用算法的性能，在同样的条件下，对本文的算法也进行了编译，得到了最高工作频率信息。最终结果如表1所示。采用IP核进行关键路径的计算，最高工作频率为114.745 MHz。采用优化后的CORDIC算法进行关键路径的计算，最高频率为187.652 MHz。相比使用IP核的方法，采用优化后的CORDIC算法实现关键路径的计算可以提速63.53％。

5 结论

    本文在传统Sobel加速算法的基础上，在FPGA平台上使用优化的CORDIC算法实现了Sobel算法加速。通过图9可知，该方法的边缘检测效果良好，较好地检测出了图像的边缘。通过表1可知，该方法与调用IP核相比提高了百分之63.53％的工作频率。实验结果表明，本设计进一步提高了系统的运算速度，适合在对速度有较高要求的系统中使用。

参考文献

[1] AGGARWAL S，MEHER P K，KHARE K.Concept，design，and implementation of reconfigurable CORDIC[J].IEEE Transactions on Very Large Scale Integration Systems，2016，24(4)：1588-1592.

[2] PRASAD N，TRIPATHY M R，DAS D S，et al.Efficient VLSI implementation of CORDIC-based direct digital synthesizer[M].Intelligent Computting，Communication and Devices.Springer India，2015.

[3] 于莉洁，孙瑜亮，缪永伟.基于深度信息局部二值模式特征的室内场景边缘检测[J].计算机辅助设计与图形学学报，2017，29(12)：2162-2170.

[4] 刘小宁，谢宜壮，陈禾，等.CORDIC算法的优化及实现[J].北京理工大学学报，2015，35(11)：1164-1170.

[5] SHUKLA R，RAY K C.Low latency hybrid CORDIC algorithm[J].IEEE Transactions on Computers，2013，63(12)：3066-3078.

[6] 李锦明，闫晓俊，江旭东，等.Sobel图像边沿检测算法的优化设计与实现[J].电子技术应用，2016，42(3)：71-73.

[7] 杨新华，寇为刚.基于FPGA的Sobel算子图像边缘检测算法[J].仪表技术与传感器，2013(1)：102-104.

[8] 杜正聪，宁龙飞.基于Sobel算法图像边缘检测的FPGA实现[J].电子技术应用，2016，42(10)：89-91.

[9] HU Y H.The quantization effects of the CORDIC algorithm[J].IEEE Transactions on Signal Processing，1992，40(4)：834-844.

作者信息:

黄  虎，杨  丁，雷宇辉，谢佳讯，陈诗瑶，邹  瑜

(成都理工大学 信息科学与技术学院，四川 成都610059）