文献标识码: A
DOI:10.16157/j.issn.0258-7998.182031
中文引用格式: 李国睿,周迪,肖海林. 时延QoS保证的D2D-based V2V车载通信功率分配方案[J].电子技术应用,2019,45(3):71-75.
英文引用格式: Li Guorui,Zhou Di,Xiao Hailin. Power allocation for D2D-based V2V vehicular communication with delay QoS guarantee[J]. Application of Electronic Technique,2019,45(3):71-75.
0 引言
相比于传统车辆自组网,基于蜂窝网的V2V通信技术具有覆盖范围更广、灵活性更高、数据传输速率更快的优点。D2D技术可用于支持V2V在蜂窝网下的通信[1](本文称作D2D-based V2V通信),使用该技术,车辆间的通信不用经过基站转发,减轻了基站的负担。蜂窝网下D2D-based V2V有Overlay和Underlay两种通信模式,前者为D2D-based V2V用户分配专用的频谱资源,而Underlay模式下D2D-based V2V用户会复用蜂窝用户的频谱资源,采用Underlay模式可大大提高频谱效率[2]。
Underlay模式下,D2D-based V2V用户和蜂窝用户使用相同的频谱资源,会有严重的同频干扰[3]。近年来,有研究人员做了相关研究[4-6],文献[4]提出一种考虑蜂窝用户干扰的功率分配算法,实现了D2D-based V2V用户的连续干扰消除,但没有考虑QoS需求。文献[5]考虑了用户的QoS需求,提出了以最大化有效容量为目的的功率分配算法,但仅考虑了单个蜂窝用户和单对D2D-based V2V用户的情况。文献[6]研究了多对D2D-based V2V共用同一频带资源的场景,提出基于D2D-based V2V 用户QoS保证的资源分配方法,实现了最大化系统吞吐量的目标,但并没有考虑蜂窝用户的存在。
实际上,蜂窝小区中有数量较多的蜂窝用户和D2D-based V2V用户。本文提出一种多个蜂窝用户多对D2D-based V2V用户场景下的功率分配方案,该方案分别考虑了蜂窝用户和D2D-based V2V用户的通信需求,采用有效容量模型满足用户的时延QoS需求,通过拉格朗日方法得到优化问题的最优解。数值仿真表明,相比于其他方案,本文提出的方案能够很好地提高系统有效容量。
1 系统模型
考虑一个基于OFDMA的蜂窝小区,包含一个基站、M个蜂窝用户和N个D2D-based V2V用户。信道划分为K个正交子信道,每个子信道带宽为B。蜂窝用户随机的分布在该小区内。用K={1,2,…,K}表示所有可用子信道的集合,C={1,2,…,M}、V={1,2,…,N}分别表示蜂窝用户的集合和D2D-based V2V用户的集合。其中M≤K、N≤M。
车辆在城市环境中行驶,系统模型如图1所示。D2D-based V2V用户复用蜂窝用户的上行资源,并且所有D2D-based V2V用户都采用Underlay模式通信。假设基站可以获得全部的CSI。
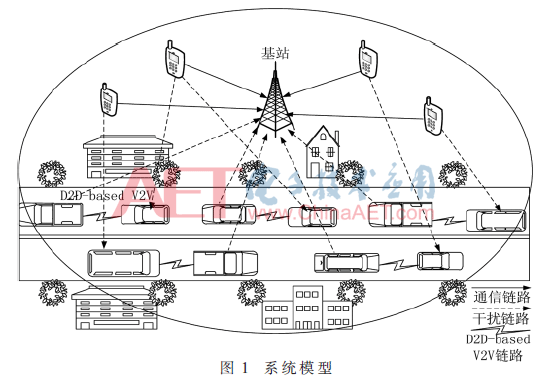
图2为D2D-based V2V用户复用蜂窝用户上行资源时的干扰模型。如图所示,系统中的干扰主要有D2D-based V2V用户发射端对基站的干扰、蜂窝用户对D2D-based V2V接收端的干扰、复用同一蜂窝用户资源的其他D2D-based V2V用户的干扰。

假设时隙长度为T,在一个时隙T内,第n个D2D-based V2V通信用户的最大服务速率为:

2 问题建模
2.1 有效容量模型
仅由物理层的信道状态信息无法满足应用层的QoS需求。对此,WU D和NEGI R在有效带宽理论的基础上提出了有效容量理论[7]。第n个D2D-based V2V用户的有效容量表达式如下:

2.2 时延QoS保证
对于车载通信业务,时延是最关键的QoS参数。根据大偏差理论[8],队列的长度可收敛至一个稳态队长:

2.3 优化问题
本文的目标是基于车载通信的低时延QoS需求,求解最优功率分配方案使得系统的有效容量最大。相应优化问题可表示为:

3 基于时延QoS保障的功率分配
3.1 拉格朗日方法
由于式(12)满足Slater准则,强对偶性成立[9]。式(12)的部分拉格朗日函数表达式如下:
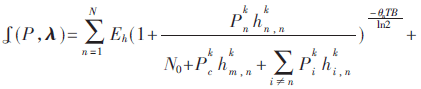

3.2 求最优对偶变量
对偶变量的最优解可采用次梯度法求解:

4 仿真分析
本文假设所有车辆都通过D2D-based V2V方式通信,所有车辆具有相同的时延QoS需求。为了便于分析,假设一个D2D-based V2V用户只复用一个蜂窝用户的资源。仿真参数的设置依据3GPP标准规定的LTE-OFDMA系统的参数[11],如表1所示。

首先验证算法的收敛性。由图3可以看出,随着迭代次数的增长,子问题Subn收敛。
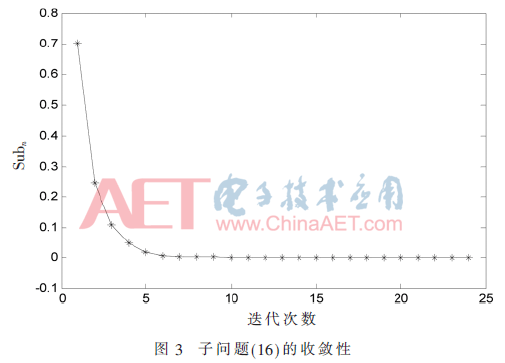
为比较性能,选取3种方案作为对比:文献[12]的和速率最大方案、文献[13]的随机功率分配方案以及文献[14]的恒定功率分配方案。
图4考察QoS参数θ对系统有效容量的影响。由图中可见,当θ变大时,系统有效容量随着θ单调递减。可以看出提出的拉格朗日对偶资源分配法具有较优性能,相比于速率最大方案,所提方案在θ为10-3和10-2处性能分别提升了14%和108%。

图5为系统有效容量受干扰D2D-based V2V用户发射功率影响的情况。随着干扰用户发射功率逐渐增大,系统有效容量呈单调递减趋势,由此可见干扰控制对提升系统性能的必要性。

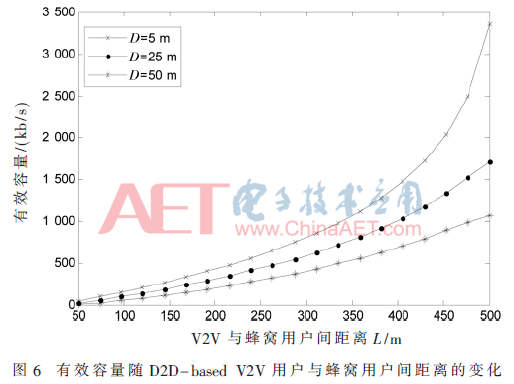
图6为D2D-based V2V用户与蜂窝用户间的距离L对有效容量的影响。其中D为车辆用户发端到收端的距离。由图6中可以看出,当L值过小时,如图中L=50,此时产生的干扰值较大,导致系统有效容量接近于0值。随着L值的增大,系统性能有明显的改善。另外可以看出有效容量随D2D-based V2V用户发端到收端的距离的增大而减小。
5 结论
本文研究了基于OFDMA小区的V2V通信,采用D2D技术支持该场景下的V2V通信。采用有效容量模型满足用户的时延QoS需求,提出了有效的功率分配算法,分别保证了蜂窝用户和车辆用户的通信需求。本文基于拉格朗日对偶法对原问题进行转换,并通过求解对偶问题,最终得到了优化函数的最优值。数值仿真表明,相比于其他方案,本文提出的方案能够很好地提高系统有效容量。
参考文献
[1] VINEL A.3GPP LTE Versus IEEE 802.11p/WAVE: which technology is able to support cooperative vehicular safety applications[J].IEEE Wireless Communication Letters,2012,1(2):125-128.
[2] Wang Wei,LAU V K N.Delay-aware cross-layer design for device-to-device communications in future cellular systems[J].IEEE Communications Magazine,2014,52(6):133-139.
[3] Li Jiandong,Huang Sheng.Delay-aware power control for D2D communication with successive interference cancellation and Hybrid energy source[J].IEEE Wireless Communications Letters,2017,6(6):806-809.
[4] Song Hojin,RYU J Y,CHOI W,et al.Joint power and rate control for Device-to-Device communications in cellular systems[J].IEEE Transactions on Wireless Communications,2015,14(10):5750-5762.
[5] Cheng Wenchi,Zhang Xi,Zhang Hailin.Optimal power allocation with statistical QoS provisioning for D2D and cellular communications over underlaying wireless networks[J].IEEE Journal on Selected Areas in Communications,2016,34(1):151-162.
[6] Mi Xiang,Xiao Limin,Zhao Ming,et al.Statistical QoS-driven power control and source adaptation for D2D communications[C].IEEE Military Communications Conference(MLCOM).Baltimore,MD,USA:IEEE Press,2016:307-312.
[7] WU D,NEGI R.Effective capacity:a wireless link model for support of quality of service[J].IEEE Transactions on Wireless Communications,2003,2(4):630-643.
[8] Chang Chengshang.Stability,queue length,and delay of deterministic and stochastic queueing networks[J].IEEE Transactions on Automatic Control,1994,39(5):913-931.
[9] BOYD S,VANDENBERGHE L.Convex optimization[M].Cambridge,UK:Cambridge University Press,2004.
[10] Zhang Rui,Cui Shuguang,Liang Yingchang.On ergodic sum capacity of fading cognitive multiple-access and broadcast channels[J].IEEE Transactions on Information Theory,2009,55(11):5161-5178.
[11] 3GPP TR 25.814V7.1.0,Physical layer aspects for evolved UTRA[S].2006.
[12] ABRARDO A,MORETTI M.Distributed power allocation for D2D communications underlaying/overlaying OFDMA cellular networks[J].IEEE Transactions on Wireless Communications,2017,16(3):1466-1479.
[13] LEE H W,MODIANO E,LE L B.Distributed throughput maximization in wireless networks via random power allocation[J].IEEE Transactions on Mobile Computing,2012,11(4):577-590.
[14] BASH B A,GOECKEL D,TOWSLEY D.Asymptotic optimality of equal power allocation for linear estimation of WSS random processes[J].IEEE Wireless Communications Letters,2013,2(3):247-250.
作者信息:
李国睿1,周 迪1,2,肖海林1
(1.桂林电子科技大学 信息与通信学院,广西 桂林541004;2.浙江宇视科技有限公司,浙江 杭州310051)

