同时具有高电子和空穴迁移率以及高导热率的半导体材料有益于提升微电子和光电子器件的性能（1，2）。然而，到目前为止，仍然没有确认同时具有高迁移率和热导率的材料。例如，应用最广泛的硅（Si）和砷化镓(GaAs)，其室温电子迁移率分别为1400cm²/(VS)和8500cm²/(VS)。然而，它们在常温环境下的空穴迁移率(Si为450cm²/(VS),GaAs为400cm²/(VS)和热导率(kRT=140W/(m·K),GaAs为45W/(m·K))，这个数据低于预期。

　　尽管石墨烯具有高电子和空穴迁移率以及高面内热导率，但其跨面热传导较低（3，4）。金刚石虽然具有最高的RT热导率和优良的电子和空穴迁移率，但是5.4 eV的禁带宽度使其难以通过常规方式进行有效掺杂（5）。

　　最近，第一性原理计算（first-principles calculations）预测立方砷化硼具有极高的常温热导率（约1400 W/(m·K)），这个数字是Si的10倍。这一高值源于其不寻常的声子散射和化学键性质，它们同时促进弱三声子（weak three-phonon）和四声子散射（four phonon scattering）。这一预测现已被实验证实，而在kRT = 1000-1300 W/(m·K)范围内测量到的立方砷化硼热导率表明，立方砷化硼是除金刚石外导热率最高的半导体材料。

　　第一性原理计算也预测了立方砷化硼应该同时具有较高的常温电子和空穴迁移率，μe =1400cm²/(VS),μh=2100cm²/(VS)。造成这种高电子和空穴迁移率的主要原因是立方砷化硼中极性光学声子的高能量和低占据，这带来了弱载流子散射。这一特性将立方砷化硼与其他III-V半导体材料区分开，除了AlSb 外(μe=200cm²/(VS)和μh= 400cm²/(VS))，其他III-V半导体具有较高的电子迁移率，但空穴迁移率低得多，其中μe/μh>10到~100，。

　　尽管理论预测十分出色，砷化硼的高迁移率并没有从实验测量中得到证实。与其他III-V族半导体的发展历史类似，立方砷化硼晶体的品质受到较大且不均匀的缺陷密度限制。传统的基于输运原理的测量方法（traditional bulk transport measurement methods）极大地受到缺陷密度的限制而不能获得材料本体的固有性质，因此立方砷化硼晶体中的高缺陷密度阻碍了此类测量评估预测的高迁移率的有效性。

　　此外，先前的研究表明，热导率和电子迁移率之间似乎没有强关联。Kim等人测量了kRT=186 W/(m·K)和μh预估为400cm?/(VS)的立方砷化硼微棒样品（microrod sample）。Chen等人测量了kRT=920 W/(m·K)和μh=22cm?/(VS)毫米尺度立方砷化硼晶体（millimeter-scale c-BAs crystals）。两者观察到的迁移率远低于计算的迁移率，且与测量的热传导率没有明显的相关性。（i）理论计算和实验之间的差异以及（ii）热性能和电性能之间解耦的原因尚未确定。

　　我们使用光学瞬态光栅（ optical transient grating (TG)）方法测量了立方砷化硼单晶同一点上的电迁移率和热导率。实验证实，立方砷化硼不但具有高热导率，同时还具备高电子和高空穴迁移率。根据理论计算，电离杂质对电荷载流子有强烈的散射作用，而中性杂质主要导致热导率降低。这些发现使立方砷化硼成为唯一已知的具有这种理想性能组合的半导体，并使其成为下一代微电子应用的理想材料。

　　我们在不同条件下使用多步化学蒸汽传输（multistep chemical vapor transport）制备立方砷化硼样品（18）（图S1和S2）。我们使用扫描电子显微镜（SEM）对厚度约为20 μm的立方砷化硼单晶进行成像（图1、a和B），并通过x射线衍射（XRD）确认了立方结构（图1C），与文献（19）一致。

　　我们使用光致发光（PL：photoluminescence）和拉曼光谱来确定立方砷化硼（17，20）中的不均匀杂质分布。我们测量了PL光谱（图1D），并对立方砷化硼晶体进行了二维（2D）PL映射（图1E）。局部亮点表明电荷载流子密度和电子与空穴复合动力学的空间差异。我们还测量了拉曼光谱（图1F），并进行了2D拉曼背景散射强度（IBG）映射（图1G）。约700cm-1处的强拉曼峰对应的是立方砷化硼区域中心处的的纵向光学（LO）模式。LO峰和IBG的半宽度可归因于杂质导致的质量无序，导致了较大的热导率的变化（11，21）。

　　我们使用TG技术（22-24）（图2A）同时测量多个点（图1，圆圈a至d）上的电输运和热输运。具有波矢量k1和k2的两个飞秒激光脉冲（pump）在立方砷化硼样品上产生正弦光学干涉，从而激发电子-空穴对（图S3）。第三个激光脉冲（k3；探针）在延迟时间t后到达样本点，随后沿k1-k2+k3方向衍射，并与用于外差检测的第四脉冲（k4）混合。当光激发载流子经历扩散和复合时，相应的衍射信号随时间衰减。我们在图2B和图2B中显示了计算出的立方砷化硼中随时间变化的电子-空穴分布。S4和S5。

　　Fig. 1. Optical characterization of c-BAs single crystals. (A) Optical photograph. (B) SEM image. (C) XRD. a.u., arbitrary units; deg, degrees. (D and E) A typical PL spectrum (D) and 2D PL intensity mapping (E) integrated over 100-nm spectrum range for each spot. The dashed circles show TG measurement spots (a to d). cps, counts per second. (F and G) A typical Raman spectrum (F) and 2D mapping of background Raman scattering intensity (G) integrated over 100 cm-1 for each spot

　　Fig. 2. Thermal and electron transport measurements. (A) Schematic illustration of TG experiments. (B) Calculated time-dependent electron-hole pair density in c-BAs. CB, conduction band; VB, valence band; Eg, bandgap. (C) TG signal for c-BAs. Thermal conductivity is calculated from exponential fitting (red line). (D) Wavelengthdependent electrical decay rate Ge and TG peak amplitude. (E) TG signal with varying diffraction grating periods q. (F) Electrical decay rate (Ge) and thermal decay rate (Gth) versus q2 . Error bars show experimental uncertainties

　　光激发载流子的扩散和复合导致TG信号的快速指数衰减（t＜1ns），随后是一个较慢的热衰减(t > 1ns)，其符号相反(图2C)。短时间衰减和长时间衰减可以用来分别计算同一点上的载流子迁移率和热导率(详见图S6)。通过长时间衰减（红线）的指数拟合直接计算导热系数。

　　电衰减对泵浦脉冲的波长敏感，我们使用光学参量放大器（OPA）将泵浦光束的波长与立方砷化硼的带隙（2.02 eV）匹配，以避免激发高能电子，从而导致具有不同散射动力学和迁移率的热电子和空穴（25）。

　　我们还确定了与波长相关的电衰减率Γe和TG峰值的锁相放大器幅度（图2D）。TG在较短波长（＜500nm）下衰减得更快，并在带隙附近达到一个平台（~600nm），随后光子能量在带隙（＞650nm）以下出现信号损失（图S7）。

　　电衰变Γe和热衰变Γth相对于q2的斜率（图2，E和F）相当于立方砷化硼的双极扩散率Da和热熔性Dth。Da随后转化为双极迁移率μa=eDa/kBT=2μeμh/（μe+μh），其主要由低迁移率载流子决定，其中kB为玻尔兹曼常数，e为基本电荷，T为温度。

　　从a点到d点，我们测量了大量的常温热导率和双极性迁移率 (a: 920 W/(m·K)和731cm²/(VS);b: 1132W/(m·K);1482cm²/(VS);d: 211 W/(m·K)和328cm²/(VS))。这种巨大的热电性质空间差异性可以归因于相应的杂质密度的变化。较高的杂质密度会降低PL强度，增加IBG。为了证实这一趋势，我们有意在立方砷化硼样本IV中掺杂了碳，热导率和双极性迁移率测量范围分别为k=200至953 W/(m·K)和μa=195至416cm²/(VS)，同时也发现了IBG的较大差异和低PL强度(图4)（S8和S9)。

　　立方砷化硼中常见的杂质是IV族元素，如C和Si。由于低形成能，这些杂质可以用作立方砷化硼中的电子受体（26）。由电离杂质产生的空间电荷在局部键合环境中引入畸变，驱动特定的声子散射机制。立方砷化硼的热导率可以通过求解声子玻尔兹曼输运方程来计算，包括三声子和四声子散射以及B或As位点（27、28）上中性（实线）和带电（虚线）IV族杂质的声子散射（图3A）。我们计算的k随着杂质和主体原子之间质量差的增加而减小。在杂质电离时，杂质（IV）的价电子数与B或As（III或V）的相匹配，导致比中性杂质弱的键扰动（weaker bond perturbations）。因此，电离杂质对热导率的降低要小于非电离杂质对热导率的降低，特别是当被取代的杂质具有与主体原子类似的质量时，即Ge–As和C+B 。

　　Fig. 3. Theoretical calculation of the impurity effects on thermal conductivity and mobility. (A and B) Calculated thermal conductivity (A) and ambipolar mobility (B) with neutral (solid lines) and charged (dashed lines) group IV impurities. Open circles are mh values of bulk samples measured by electrical probes (fig. S12). (C) Calculated electron-phonon and short- and long-range impurity scattering rates for holes. Zero of energy is at the valence band maximum. Si– As ^1/4 1018cm3. (D) Thermal conductivity (solid lines) and mobility (dashed lines) differences between charged and neutral impurities

　　杂质的键微扰（bond perturbation）和库仑势（Coulomb potential）对立方砷化硼中的电子和空穴传输动力学有不同的影响。基于计算带电杂质形成能的最新进展（29），我们使用从头计算方法来研究IV族杂质对立方砷化硼常温双极性迁移率的影响（图3B）。我们展示了含的立方砷化硼中空穴的电子-声子散射和长程和短程缺陷散射（详见图S10）（图3C）。在带边附近，与带电杂质的长程库仑相互作用是主要的散射机制。中性杂质缺乏库仑电势会导致较弱的载流子散射，导致μa在浓度接近1018 cm-3时才下降，此时电子-中性杂质散射开始显示影响。然而，无论杂质的质量如何，带电杂质的μa从1016 cm-3显著降低。

　　我们阐明了中性杂质和带电杂质对k和μa的不同影响（图3D）。与带电杂质相比，中性杂质更强烈地抑制k，因为键扰动更强（27）。由于库仑散射，不管质量如何，带电杂质主要有助于μa还原。质量与主原子相似的带电杂质将表现出常温热导率高于1000 W/(m·K)，即使在1019cm-3的高杂质密度下，且μa显著降低至低于400cm²/(VS).中等水平1018cm-3。

　　我们还可以突出k和μa与批次0至IV的中性和带电杂质的对比趋势（图4A和表S1）（18）。图4中的实线和虚线分别显示了中性Si0 As和带电Si–As计算的μa和k轨迹，从1016到1020 cm-3。散射点是不同批次样品的测量μa和k值，用不同颜色标记。所有测量数据都拟合到轨迹曲线之间的区域中。

　　在高质量立方砷化硼批次（III）中，我们测量得到的μa=1600±170cm²/(VS)，k=1200±130 W/(m·K).我们还测量了高质量样品的两个不同点（III-a和III-b）的温度相关μa（图S11），测得的III-a的μa与计算结果一致（图4B）。散装样品（the bulk samples）的的霍尔测量提供了μh和载流子浓度p，其在整个样品上具有空间变化的杂质浓度。图3B中绘制的测量体μh（详细信息参见图S12）受到平均杂质浓度的限制，而不是杂质含量低的局部点。

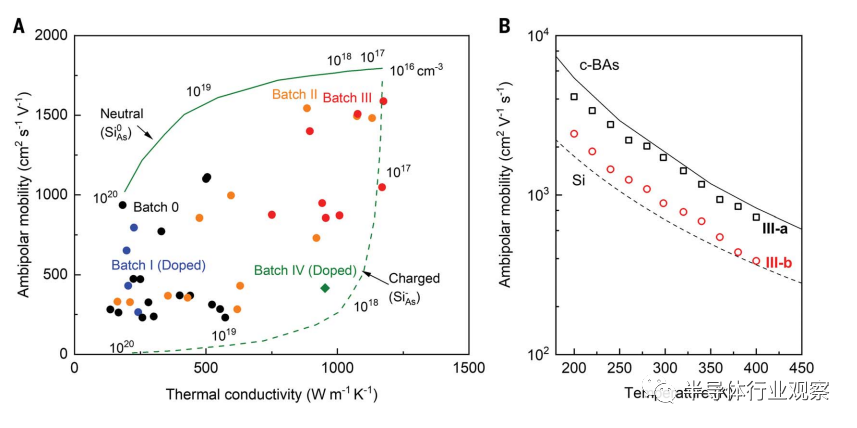
　　Fig. 4. Ambipolar mobility and thermal conductivity of c-BAs. (A) Measured mobility and thermal conductivity of c-BAs from different batches (batches 0, I, II, III, and IV). See table S1 for details. The solid and dashed lines show the calculated ma and k with varying concentrations of neutral Si0 As and charged Si– As, respectively. Typical uncertainties for ma and k are 11%. (B) Temperaturedependent ambipolar mobility of c-BAs (III-a and III-b). The solid and dashed lines show calculated ma of pristine c-BAs and Si, respectively (32).

　　高空间分辨率的热重测量为立方砷化硼中同时存在高电子和空穴迁移提供了明确的证据，并表明通过消除缺陷和杂质，立方砷化硼可以表现出高的热导率和高电子和空穴迁移率。此外，观察到的局部热导率和迁移率之间的微弱相关性是由中性和电离杂质对这些量的不同影响造成的。这种电子和热性能的显著结合，以及与常见半导体(如Si和GaAs)密切匹配的热膨胀系数和晶格常数(30,31)，使立方砷化硼成为一种有前景的，可以用于集成当前和未来半导体制造工艺的材料，并能够解决下一代电子在热管理方面的挑战。

　　备注：感谢复旦大学工程与应用技术研究院雷光寅博士的审核与指导。

　　作者：Jungwoo Shin, Geethal Amila Gamage, Zhiwei Ding, Ke Chen, Fei Tian , Xin Qian, Jiawei Zhou, Hwijong Lee, Jianshi Zhou , Li Shi , Thanh Nguyen , Fei Han , Mingda Li , David Broido , Aaron Schmidt , Zhifeng Ren *, Gang Chen

　　参考文献和注释

　　1. X. Qian, J. Zhou, G. Chen, Nat. Mater. 20, 1188–1202 (2021).

　　2. G. Chen, Nat. Rev. Phys. 3, 555–569 (2021).

　　3. K. S. Novoselov et al., Science 306, 666–669 (2004).

　　4. A. A. Balandin et al., Nano Lett. 8, 902–907 (2008).

　　5. C. J. H. Wort, R. S. Balmer, Mater. Today 11, 22–28 (2008).

　　6. L. Lindsay, D. A. Broido, T. L. Reinecke, Phys. Rev. Lett. 111, 025901 (2013).

　　7. D. A. Broido, L. Lindsay, T. L. Reinecke, Phys. Rev. B 88, 214303 (2013).

　　8. T. L. Feng, L. Lindsay, X. L. Ruan, Phys. Rev. B 96, 161201 (2017).

　　9. J. S. Kang, M. Li, H. Wu, H. Nguyen, Y. Hu, Science 361, 575–578 (2018).

　　10. F. Tian et al., Science 361, 582–585 (2018).

　　11. S. Li et al., Science 361, 579–581 (2018).

　　12. T. H. Liu et al., Phys. Rev. B 98, 081203 (2018).

　　13. D. L. Rode, Phys. Rev. B 3, 3287–3299 (1971).

　　14. A. Nainani, B. R. Bennett, J. B. Boos, M. G. Ancona, K. C. Saraswat, J. Appl. Phys. 111, 103706 (2012).

　　15. J. I. Pankove, T. D. Moustakas, Semicond. Semimet. 50, 1–10 (1997).

　　16. J. Kim et al., Appl. Phys. Lett. 108, 201905 (2016).

　　17. X. Chen et al., Chem. Mater. 33, 6974–6982 (2021).

　　18. Materials and methods are available as supplementary materials online.

　　19. J. A. Perri, S. Laplaca, B. Post, Acta Cryst. 11, 310 (1958).

　　20. S. Yue et al., Mater. Today Phys. 13, 100194 (2020).

　　21. A. Rai, S. Li, H. L. Wu, B. Lv, D. G. Cahill, Phys. Rev. Mater. 5, 013603 (2021).

　　22. A. A. Maznev, T. F. Crimmins, K. A. Nelson, Opt. Lett.

　　23, 1378–1380 (1998). 23. A. A. Maznev, K. A. Nelson, J. A. Rogers, Opt. Lett. 23, 1319–1321 (1998).

　　24. S. Huberman et al., Science 364, 375–379 (2019).

　　25. K. Chen et al., Carbon 107, 233–239 (2016).

　　26. J. L. Lyons et al., Appl. Phys. Lett. 113, 251902 (2018).

　　27. M. Fava et al., Npj Comput. Mater. 7, 54 (2021).

　　28. M. Fava et al., How dopants limit the ultrahigh thermal conductivity of boron arsenide: A first principles study, version 1, Zenodo (2021); https://doi.org/10.5281/zenodo.4453192.

　　29. C. Freysoldt et al., Rev. Mod. Phys. 86, 253–305 (2014).

　　30. F. Tian et al., Appl. Phys. Lett. 114, 131903 (2019).

　　31. X. Chen et al., Phys. Rev. Appl. 11, 064070 (2019). 32. N. D. Arora, J. R. Hauser, D. J. Roulston, IEEE Trans. Electron Dev. 29, 292–295 (1982).

　更多信息可以来这里获取==>>电子技术应用-AET<<