蛋白质结构预测问题是当今最具有挑战和研究价值的课题之一。蛋白质工程正在发展成为可能影响人类生活许多方面的生物高技术。蛋白质工程的根本目的就是希望能够根据人类的需要设计并制造出具有特定功能的非天然蛋白质。
　　蛋白质的生物学功能取决于蛋白质的空间折叠结构。自上世纪50年代末以来，C.B.Anfinsen，K.A.Dill 及K.F.Lau等人^[1～3]就发现蛋白质的空间折叠结构取决于构成该蛋白质的氨基酸的序列。也就是说蛋白质的空间折叠结构的全部信息都隐藏在蛋白质线性结构中，即氨基酸序列中。因此，从理论上讲人们可以通过控制蛋白质的氨基酸序列来控制蛋白质的空间折叠结构，从而控制所设计制造出的蛋白质的生物学功能。
1 用于蛋白质结构预测的三维连续数学模型
　　连续模型^[4]的描述为：对于任意给定的正整数n和任意地被确定了黑白颜色标号分别为1，2，……n的n个半径为0.5的小球(h代表黑球，p代表白球)，如何调整这n个球的球心在三维欧氏空间中的位置，才能使这n个球两两互不嵌入，标号相邻的两个球皆相切，并且使其按如下公式(1)计算处于能量最低的状态，即值越小越好。

　　此问题更为形式化的提法是寻求3n个实数x₁，y₁，z₁，……x_n，y_n，z_n，使其在如下约束关系(4)，(5)得到满足的条件下，(1)式达到最小值。
　　
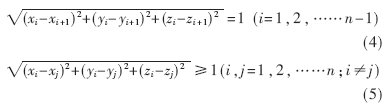
　　在此数学模型" title="数学模型">数学模型中，黑球h代表疏水氨基酸，白球p代表亲水氨基酸；长度为n的黑白球序列代表蛋白质氨基酸序列。数学模型(1)～(5)的解(x₁，y₁，z₁，……x_n，y_n，z_n)即为所求蛋白质在三维空间中的折叠结构。
2 求解蛋白质结构预测问题的拟物拟人算法
2.1 拟物算法的简述
　　在C.B.Anfinsen，K.A.Dill及Hsian-Ping Hsu等人的原始发现和后续工作的基础^[1～4]之上，受到他们的启发同时也观察到他们在实际中所遇到的困难，结合作者自身NP-hard问题求解中的经验^[5～8]提出如下的物理模型：将(1)～(5)式中涉及到的n个半径为0.5的球想象为光滑的弹性实体，想象第i个球与第i+1个球的球心之间有一根原始长度为1的弹簧相连(i=1，2，3，……n-1)。并且每个黑球和当前所有小球形成的系统的几何中心有一根原长为RR(RR为任意给的一个实数)的弹簧相连。设想这n个球现在被随机地撒在空间中。这样整个系统就会具有如下能量：
　　①编号不相邻的小球之间的万有引力所引起的引力势能；
　　②编号相邻的三个小球之间的角度所引起的角度势能；
　　③编号相邻的两个小球之间的弹簧拉力所引起的弹簧势能；
　　④编号不相邻的两个小球相互嵌入时所引起的嵌入势能；
　　⑤每个黑球和所有小球形成系统几何中心弹簧拉力所引起的弹簧势能。
　　在此过程中新加入的弹簧势能③和嵌入势能④的作用是在运动中逐渐使约束条件" title="约束条件">约束条件(4)和(5)得以满足，而黑球和系统几何中心的弹簧势能是笔者在实践工作中了解到黑球聚在一起时能量会更低些，因此这里加入了此能量来加快黑球聚拢。
　　在此拟物的思想下本文把在满足(4)和(5)式的条件下求解(1)式的最小值转换为求如下式子的最小值：
　　
　　其中U₁为(1)式中的能量E的值，n为黑白球总数，m为黑球的总数。
2.2 模型中新加入的能量分析及其物理意义
　　(1)相邻小球i和小球i+1之间的弹簧拉力所引起的弹簧势能如下：

2.3 模型的求解方法
　　经过以上的拟物处理后能量表达式(1)转换为(6)式在三维欧氏(x₁，y₁，z₁，……x_n，y_n，z_n)空间无约束条件的情况下求最小值。这里采用沿梯度的反方向运动求其最小值。其体系的运动方程为：

2.4 跳坑的拟人策略
　　由于在计算过程中往往会遇到这样的情况：各球均以其平衡位置为中心微幅振动，趋于静止，并且满足(4)和(5)这两个约束条件，但是其能量很高，可以把这种情形看成是计算落入了局部极小值。
　　为解脱此种困境，纯粹的拟物方法是重新选取初始值，然后进行新一轮的拟物计算。这样虽然具有最终的收敛性质，但是实算的经验说明其效率是低的。此时好的办法是提出一种有效的“跳出陷阱”的策略，将计算点从局部极小值的陷阱中取出，而置入更有前景的位置上，然后进行新的拟物计算。这种“跳出陷阱”的策略可通过观察与体会人类社会的生活经验得出，因而被称为拟人策略^[8]。
　　在拥挤的公共汽车中，受挤压者总是设法改换自己的位置。这里将n个小球和三维空间看成是一个公共汽车的车厢，于是对以上乘车现象的观察启发笔者得出以下策略。
　　计算出每个黑球和其他小球间的引力势能，这样一定有一个黑球S的引力势能值最小，可以认为它处于很舒服的地方因此不动它。而其他的黑球按照它们相对于黑球S的引力势能值越大被选中的概率也越大来选择其中的一个黑球，这里给这个被选中的黑球和它相邻的几个小球的坐标一个微小的变动来破坏当前的系统，在此基础上开始进行拟物计算。
2.5 拟物拟人算法
　　(1)初始值的选取
　　对每一个小球以等概率产生0到1之间的三个随机数α，β，γ，若其为黑球则用α*R，β*R，γ*R(R为任意给定的一个实数)分别作为该球的x，y，z的坐标。若为白球则用α*R+R，β*R+R及γ*R+R分别作为该球的x，y，z的坐标。这样所有的黑球落在半径为R的球内，所有的白球落在半径为R和半径为2R的球环中" title="环中">环中。